Cho tam giác ABC vuông tại A đường cao AH. Gọi M, N lần lượt là hình chiếu của H lên AB và AC

Cho tam giác ABC vuông tại A đường cao AH. Gọi M, N lần lượt là hình chiếu của H lên AB và AC

Nguyễn Mạnh Tài Ngày: 10-05-2024 Tổng hợp kiến thức

149

Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 96)

Đề bài. Cho tam giác ABC vuông tại A đường cao AH. Gọi M, N lần lượt là hình chiếu của H lên AB và AC. Chứng minh rằng $\frac{S_{A M N}}{S_{A B C}} = \sin^{2} B . \sin^{2} C$ .

Lời giải:

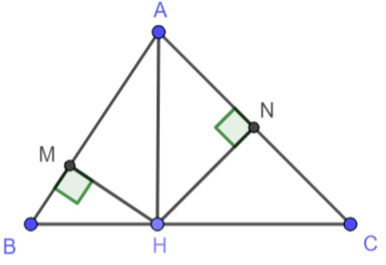Ta có: HM ⊥ AB, HN ⊥ AC, AB ⊥ AC

Nên AMHN là hình chữ nhật

⇒ AH = MN

⇒ $\hat{A M N} = \hat{M A H} = \hat{B A H} = 90^{\circ} - \hat{B} = \hat{A C B}$

Mà $\hat{M A N} = \hat{B A C}$

⇒ ∆ANM ∽ ∆ABC (g.g)

⇒ $\frac{S_{A M N}}{S_{A B C}} = {(\frac{M N}{B C})}^{2} = \frac{A H^{2}}{B C^{2}}$
Ta có: 1 – cos²B = sin²B

⇒ (1 – cos²B)sin²C = sin²Bsin²C = (sinBsinC)²

= ${(\frac{A C}{B C} . \frac{A B}{B C})}^{2} = {(\frac{A B . A C}{B C^{2}})}^{2} = {(\frac{A H . B C}{B C^{2}})}^{2} = {(\frac{A H}{B C})}^{2}$

⇒ $\frac{S_{A M N}}{S_{A B C}} = (1 - - c o s^{2} B) s i n^{2} C$

⇒ $\frac{S_{A M N}}{S_{A B C}} = \sin^{2} B . \sin^{2} C$

Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:

Đề bài. Cho hình bình hành ABCD, hai đường chéo cắt nhau ở O. Hai đường thẳng d₁ và d₂ cùng đi qua O và vuông góc với nhau. Đường thẳng d₁ cắt các cạnh AB và CD ở M và P. Đường thẳng d₂ cắt các cạnh BC và AD ở N và Q.

Đề bài. Cho hình thang ABCD (AB // CD) có AB = 1cm, CD = 5cm và $\hat{C} = 30 °, \hat{D} = 60 °$ . Tính diện tích hình thang ABCD.

Đề bài. Cho hình thang cân ABCD có đáy lớn AB = 30 cm, đáy nhỏ CD = 10 cm và $\hat{A}$ = 60°. Tính cạnh BC.

Đề bài. Cho hình thoi ABCD có cạnh AB = 8cm. Tính chu vi hình thoi ABCD?

Đề bài. Mảnh vườn hình chữ nhật ABCD có kích thước như hình vẽ. Ở chính giữa mảnh vườn người ta xây 1 cái chòi hình vuông EFGH có cạnh EH = 2m; một lối đi ra chòi hình bình hành DHIK có cạnh DK = 1m.

Đề bài. Cho chóp S.ABCD có đáy hình bình hành tâm O. Lấy N, M lần lượt thuộc SA, SB sao cho $B M = \frac{1}{4} B S, S N = \frac{3}{4} S A$ . Tìm giao tuyến của:

Đề bài. Cho tam giác ABC vuông tại A đường cao AH. Gọi M, N lần lượt là hình chiếu của H lên AB và AC. Chứng minh rằng $\frac{S_{A M N}}{S_{A B C}} = \sin^{2} B . \sin^{2} C$ .

Đề bài. Trên mặt phẳng tọa độ cho các điểm A, B, C có tọa độ A(0; 4), B(3; 4), C(3; 0). Hãy tìm hệ số a sao cho đường thẳng y = ax chia hình chữ nhật OABC thành hai phần, trong đó diện tích phần chứa điểm A gấp đôi diện tích phần C.

Đề bài. Tính diện tích của hình H gồm hình bình hành ABCD và hình chữ nhật DCNM, biết hình chữ nhật DCNM có chu vi bằng 180 cm và chiều dài MN gấp 4 lần chiều rộng CN.

Đề bài. Cho a, b, c là các số thực dương thỏa mãn log₂a + log₈b + log₃₂c = 10 và $\sqrt{a} = \sqrt[3]{b} = \sqrt[5]{c}$ . Tính log₄(abc).

Đề bài. Cho ba điểm A(-1; -1), B(0; 1), C(3; 0). Xác định tọa độ điểm D biết D thuộc đoạn thẳng BC và 2BD = 5DC.

Đề bài. Cho tứ giác ABCD có CD = 24cm. O là giao điểm của hai đường chéo. Tính diện tích tứ giác biết khoảng cách từ A, B, O đến CD theo thứ tự bằng 20cm, 15cm, 12cm.

Đề bài. Cho tứ giác ABCD. M, N là trung điểm của AC và BD.

Chứng minh: AB²+ BC² + CD² + DA² = AC² + BD² + 4MN².

Đề bài. Trong không gian Oxyz, cho mặt cầu (S) có tâm I(−2; 1; 2) và đi qua điểm A(1;−2; −1). Xét các điểm B, C, D thuộc (S) sao cho AB, AC, AD đôi một vuông góc với nhau. Thể tích của khối tứ diện ABCD có giá trị lớn nhất bằng?

Đề bài. Tìm m để đồ thị hàm số y = x⁴– (1 + 9m²)x² + 9m² cắt trục hoành tại 4 điểm phân biệt có hoành độ lập thành cấp số cộng.

Đề bài. Doanh thu (triệu đồng) của công ty A khi sản xuất và bán x sản phẩm được cho bởi: R(x) = −3x² + 140x đôla. Tính doanh thu của công ty khi khi sản xuất bán sản phẩm thứ 10?

Đề bài. Tính $(\frac{1}{4.9} + \frac{1}{9.14} + \frac{1}{14.19} + \dots + \frac{1}{44.49}) . \frac{1 - 3 - 5 - 7 - \dots - 49}{89}$ .

Đề bài. Tính giá trị biểu thức: $(- \frac{3}{4} + \frac{6}{13}) . \frac{9}{4} - (\frac{13}{3} - \frac{7}{13}) . \frac{4}{9}$ .

Đề bài. Rút gọn biểu thức: $\frac{1}{2 - \sqrt{x}} - \frac{1}{\sqrt{x} + 2} - \frac{x}{x - 4}$ .

Đề bài. Tìm x nguyên biết 2x + 4 chia hết cho x + 1.

Đề bài. Rút gọn biểu thức (3x + 1)²– 2(3x + 1)(3x + 5) + (3x + 5)².

Đề bài. Giải phương trình: $\sqrt{1 - x^{2}} = x - 1$ .

Đề bài. Cho hệ phương trình ${\begin{matrix} (m - 1) x - m y = 3 m - 1 \\ 2 x - y = m + 5 \end{matrix}$ .

Tìm m để có nghiệm duy nhất (x; y) sao cho biểu thức S = x² + y² đạt giá trị nhỏ nhất.

Đề bài. Tìm x biết (x + 1)⁵ = 243.

Đề bài. Tìm x biết ${(x - \frac{1}{2})}^{2} - \frac{1}{3} = \frac{22}{12}$ .

Đề bài. Tìm x biết (x – 3)³ – (x – 3)(x² + 3x + 9) + 9(x + 1)² = 15.

Đề bài. Phân tích thành nhân tử: 12x² – 72x + 60.

Đề bài. 2 ngày 16 giờ = … ngày.

Đề bài. Tính giá trị biểu thức: $\frac{1}{\sqrt{5} - 2} + \frac{1}{\sqrt{5} + 2}$ .

Đề bài. Lấy số 196 chia cho số nguyên a rồi cộng thêm a. Sau đó, lấy kết quả này chia cho a rồi cộng thêm a. Kết quả thu được là 26a. Hãy tìm a.

Đề bài. Tìm tất cả các giá trị thực của tham số m để hàm số y = x³ – 3mx² – 9m²x nghịch biến trên khoảng (0; 1).

Đề bài. Tìm các giá trị của m để phương trình x² – 2(m – 1)x + 2m – 3 = 0 có 2 nghiệm phân biệt x₁, x₂ thỏa mãn $| x_{1} - x_{2} | = 5$ với m là tham số.

Đề bài. Xác định tính đúng sai của các mệnh đề sau và tìm mệnh đề phủ định của nó.

Q: “∃n ∈ ℕ, n chia hết cho n + 1”.

Đề bài. Tìm 3 giá trị của x biết $0, 2 < x < \frac{3}{10}$ .

Đề bài. Tính giá trị biểu thức A = $1 + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!}$ .

Đề bài. Chứng minh $\frac{1}{2^{2}} + \frac{1}{3^{2}} + \dots + \frac{1}{100^{2}} < 1$ .

Đề bài. Tính A = 1 + 2 + 2² + 2³ + … + 2²⁰²¹.

Đề bài. Chứng minh rằng: 10⁹ + 10⁸ + 10⁷ chia hết cho 222 và chia hết cho 555.

Đề bài. Chứng minh rằng: 13ⁿ − 1 chia hết cho 12.

Đề bài. Tìm 2 số hữu tỉ a và b, sao cho a + b = ab = a : b.

Đề bài. Chứng minh 19¹⁹ + 69¹⁹ chia hết cho 44.

Đề bài. Chứng minh 2²⁰²⁰ + 2²⁰²¹ + 2²⁰²² + 7²⁰²³ + 7²⁰²⁴ chia hết cho 7.

Đề bài. Tìm số tự nhiên n để 2n + 3 chia hết cho 3n + 1.

Đề bài. Tìm số tự nhiên n để 3n + 4 chia hết cho n – 1.

Đề bài. Tìm tất cả các số tự nhiên x biết 3x - 12 chia hết cho x – 2.

Đề bài. Cho A = 2 . 4 . 6 . 8 . 10 . 12 + 40. Hỏi A có chia hết cho 80 không? Vì sao?

Đề bài. Cho góc $\hat{A O B}$ và góc $\hat{B O C}$ là hai góc kề bù. Biết góc $\hat{B O C}$ bằng năm lần góc $\hat{A O B}$ .

Đề bài. Điền chữ số vào dấu * để:

Đề bài. Điền chữ số vào dấu * để:

Đề bài. Viết chữ số thích hợp vào ô trống để được: 1…8 chia hết cho 9.

Đề bài. Cho hình vuông ABCD có cạnh 14cm (hình bên). Như vậy, phần tô đen trong hình vuông ABCD có diện tích là?

Đề bài. Một lớp học có 20 học sinh nam và 24 học sinh nữ. Có thể chia lớp đó thành nhiều nhất bao nhiêu tổ để số nam và số nữ được chia đều vào các tổ? Khi đó mỗi tổ có bao nhiêu nam, bao nhiêu nữ?

Đề bài. Một phòng học hình chữ nhật có chiều dài 15m và chiều rộng 7m. Người ta mua loại gạch hình vuông có cạnh 0,5m để lát nền toàn bộ phòng học. Tính số viên gạch cần dùng để lát đủ phòng học đó.

Đề bài. Để lát nền một căn phòng hình chữ nhật có chiều dài 27m, chiều rộng 15m, Người ta cần dùng một số viên gạch hình vuông có cạnh 30cm. Số viên gạch cần dùng là?

Đề bài. Tìm tập xác định $\tan (x - \frac{π}{4})$ .

Đề bài. Cho $\sin α + \cos α = \frac{1}{2}$ . Tính sin2α, cos2α, tan2α, cot2α.

Đề bài. Chứng minh $1 + \tan^{2} α = \frac{1}{\cos^{2} α}$ .

Đề bài. Tính giá trị đúng của $\tan \frac{π}{24} + \tan \frac{7 π}{24}$ .

Đề bài. Phương trình $t a n x + t a n (x + \frac{π}{3}) + t a n (x + \frac{2 π}{3}) = 3 \sqrt{3}$ tương đương với phương trình nào?

Đề bài. Tìm tập xác định của hàm số y = tanx – cot2x.

Đề bài. Khai triển đẳng thức (a + b + c)².

Đề bài. Khai triển đẳng thức (a + b + c)³.

Đề bài. Tìm 6 chữ số khác nhau a, b, c, d, e, g sao cho $A = \bar{a b c} - \bar{\deg}$ có giá trị nhỏ nhất.

Đề bài. Biết hàm số bậc hai y = ax² + bx + c có đồ thị là một đường parabol đi qua điểm A(-1; 0) và có đỉnh B(1; 2). Khi đó, giá trị biểu thức T = a + b + c bằng bao nhiêu?

Đề bài. Viết công thức tổng quát nhân xác suất P(A.B.C) trong trường hợp A, B, C độc lập với nhau

Đề bài. Tìm a và b biết C = $\bar{20 a 4 b}$ chia hết cho 45.

Đề bài. Tính tổng A = 1 + 2 + 3 + … + 100.

Đề bài. Tính tổng dãy số 1 + 2 + 3 + 4 + … + 99.

Đề bài. Với 5 chữ số 1,2,3,4,5 ta có thể viết được bao nhiêu số có: ba chữ số mà các chữ số có thể được lặp lại.

Đề bài. So sánh $\frac{2008}{2009} + \frac{2009}{2010} + \frac{2010}{2011} + \frac{2011}{2008}$ và 4.

Đề bài. Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số $y = \frac{1}{3} x^{3} - x^{2} + (m - 1) x + 2$ có hai điểm cực trị đều nằm bên trái trục tung.

Đề bài. Cho A = 1 + 2 + 2² + … + 2⁵⁰. Hãy chứng tỏ A + 1 là một lũy thừa của 2.

Đề bài. Tính giá trị biểu thức A = 1 + 2 + 3 + … + 2011.

Đề bài. Tính nhanh 1 + 2 + 3 + … + 59 + 60.

Đề bài. Một căn phòng hình chữ nhật có chiều dài 8m, chiều rộng bằng $\frac{3}{4}$ chiều dài. Để lát nền căn phòng đó. Người ta dùng loại gạch men hình vuông cạnh 4dm.

Đề bài. Cho hệ phương trình ${\begin{matrix} x + m y = 2 \\ m x - 2 y = 1 \end{matrix}$ .

Tìm các số nguyên m để hệ có nghiệm duy nhất (x; y) mà x; y là các số nguyên.

Đề bài. Tìm x biết (2x – 3)² = 9.

Đề bài. Rút gọn (3x + 2)(3x – 2).

Đề bài. Tìm x biết (3x – 2⁴).7³ = 2.7⁴.

Đề bài. Cho hình vuông ABCD. Tính giá trị $(\vec{A B} + \vec{A C} + \vec{A D}) (\vec{D A} + \vec{D B} + \vec{D C})$ .

Đề bài. Tính $\sqrt{2 - \sqrt{3}} . (\sqrt{6} + \sqrt{2})$ .

Đề bài. Rút gọn biểu thức $P = (\frac{8 - x \sqrt{x}}{2 - \sqrt{x}} + 2 \sqrt{x}) {(\frac{2 - \sqrt{x}}{2 + \sqrt{x}})}^{2}$ .

Đề bài. Tìm x biết (x + 7)(2x – 6) = 0.

Đề bài. Cho 2 số x,y thỏa mãn đẳng thức $(x + \sqrt{x^{2} + 2020}) (y + \sqrt{y^{2} + 2020}) = 2020$ . Tính x + y.

Đề bài. Chứng minh rằng $\frac{x^{2}}{y^{2}} + \frac{y^{2}}{x^{2}} + 4 \geq 3 (\frac{x}{y} + \frac{y}{x})$ .

Đề bài. Tìm x biết x² – 4 + (x – 2)(3 – 2x) = 0.

Đề bài. Khai triển biểu thức (–x – 3y)³ ta được?

Đề bài. Rút gọn biểu thức (x – y + z)² + (z – y)² + 2(x – y + z)(y – z).

Đề bài. Cho hàm số y= f(x). Đồ thị hàm số y= f’(x) như hình dưới và f(-2) = f( 2) = 0.

Đề bài. Một khu rừng hình chữ nhật có chu vi 7km 5 hm, chiều rộng bằng $\frac{2}{3}$ chiều dài. Tính diện tích khu rừng đó với đơn vị đo là mét vuông, là héc-ta.

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 5

Bài tập cuối tuần Toán lớp 5 Kết nối tri thức Tuần 35

Bài tập cuối tuần Toán lớp 5 Kết nối tri thức Tuần 35 Nguyễn Mạnh Tài

15

Toán Lớp 5

Bài tập cuối tuần Toán lớp 5 Kết nối tri thức Tuần 34

Bài tập cuối tuần Toán lớp 5 Kết nối tri thức Tuần 34 Nguyễn Mạnh Tài

18

Toán Lớp 5

Bài tập cuối tuần Toán lớp 5 Kết nối tri thức Tuần 33

Bài tập cuối tuần Toán lớp 5 Kết nối tri thức Tuần 33 Nguyễn Mạnh Tài

17

Toán Lớp 5

Bài tập cuối tuần Toán lớp 5 Kết nối tri thức Tuần 32

Bài tập cuối tuần Toán lớp 5 Kết nối tri thức Tuần 32 Nguyễn Mạnh Tài

17

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack57. All Rights Reserved.