Cho hai đường tròn (O; R) và (O'; R') (R > R') tiếp xúc ngoài nhau tại A. Qua A kẻ hai cát tuyến BD và CE (B, C ∈ (O'))

Cho hai đường tròn (O; R) và (O'; R') (R > R') tiếp xúc ngoài nhau tại A. Qua A kẻ hai cát tuyến BD và CE (B, C ∈ (O'))

Nguyễn Mạnh Tài Ngày: 27-03-2024 Tổng hợp kiến thức

268

Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 92)

Đề bài. Cho hai đường tròn (O; R) và (O'; R') (R > R') tiếp xúc ngoài nhau tại A. Qua A kẻ hai cát tuyến BD và CE (B, C ∈ (O')); D, E ∈ (O)). Chứng minh: $\hat{A B C} = \hat{A D E}$ .

Lời giải:

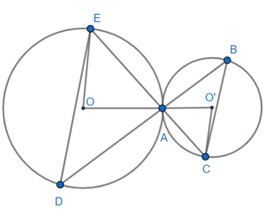
Xét tam giác O'AC có O'A = O'C = R' nên tam giác O'AC cân tại O'

Suy ra: $\hat{C O' A} = 180 ° - 2 \hat{O' A C}$

Tương tự: tam giác OAE cân tại O nên: $\hat{E O A} = 180 ° - 2 \hat{O A E}$

Mà $\hat{O' A C}, \hat{O A E}$ là 2 góc đối đỉnh nên $\hat{O' A C} = \hat{O A E}$

Suy ra: $\hat{C O' A} = \hat{E O A}$

Xét tam giác O'CA và OAE có:

$\frac{O A'}{O A} = \frac{O C'}{O C} = \frac{R'}{R}$

$\hat{C O' A} = \hat{E O A}$

⇒ ∆O'AC ∽ ∆OAE (c.g.c)

Suy ra: $\hat{A O E} = \hat{A O' C}$

Mà: $\hat{A O E} = 2 \hat{A D E}$ (vì $\hat{A O E}$ là góc ở tâm, chắn cung $\overset{⏜}{A E}$ , $\hat{A D E} = \frac{1}{2} \overset{⏜}{A E}$ )

Và $\hat{A O' C} = 2 \hat{A B C}$ (vì $\hat{A O' C}$ là góc ở tâm, chắn cung $\overset{⏜}{A C}$ , $\hat{A B C} = \frac{1}{2} \overset{⏜}{A C}$ )

Suy ra: $\hat{A B C} = \hat{A D E}$ .

Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:

Đề bài. Cho A = (m; m + 3) và B (2; 6m + 1). Tìm m để A ∩ B = ∅.

Đề bài. Cho hai tập hợp khác rỗng A = [m – 1; 5) và B = [-3; 2m + 1]. Tìm m để A ⊂ B.

Đề bài. Cho tam giác ABC cân tại A, đường cao AD, K là trung điểm của AD. Gọi I là hình chiếu của điểm D trên CK. Chứng minh rằng $\hat{A I B} = 90 °$ .

Đề bài. Cho tam giác ABC có 3 góc nhọn. Chứng minh sinA + cosA + sinC + cosC > 2.

Đề bài. Cho tam giác nhọn ABC. Chứng minh

$S_{A B C} = \frac{1}{2} . B C . B A . \sin \hat{B} = \frac{1}{2} . A B . A C . \sin \hat{A} = \frac{1}{2} . C A . C B . \sin \hat{C}$ .

Đề bài. Hình vẽ cho biết tam giác ABC vuông tại A, MN // BC, AB = 24cm, AM = 16cm, AN = 12cm. Tính độ dài x, y của các đoạn thẳng NC, BC.

Đề bài. Cho hình thoi ABCD có $\hat{A} = 60 °$ . Trên AB, AC lấy điểm M, N sao cho BM = CN. Chứng minh rằng MDN là tam giác đều.

Đề bài. Cho hình bình hành ABCD có $\hat{A} = 120 °$ . Tia phân giác của $\hat{D}$ qua trung điểm I của AB. Kẻ AH vuông góc với DC. Chứng minh rằng:

Đề bài. Cho B = 1 + 5 + 5² + … + 5¹⁰⁰. Hỏi 4B + 1 có phải số chính phương không?

Đề bài. Cho 3 số dương x, y, z có tích bằng 144. Tìm GTNN của biểu thức

Đề bài. Cho 7 số tự nhiên khác nhau có tổng bằng 100. Chứng minh rằng trong 7 số luôn có 3 số mà tổng của chúng lớn hơn hoặc bằng 50.

Đề bài. Cho biết $\cos α = - \frac{2}{3}$ . Tính giá trị của $P = \frac{\cot α + 3 \tan α}{2 \cot α + \tan α}$ .

Đề bài. Với x > 0 cho biểu thức $A = \frac{1}{\sqrt{x}} + \frac{\sqrt{x}}{\sqrt{x} + 1}; B = \frac{\sqrt{x}}{x + \sqrt{x}}; P = \frac{A}{B}$ .

Đề bài. Cho biểu thức: $A = \frac{1}{\sqrt{x} + 1} + \frac{x}{\sqrt{x} - x}$ với x > 0, x khác 1.

Đề bài. Cho biểu thức $B = \frac{\sqrt{a}}{\sqrt{a} - 3} - \frac{3}{\sqrt{a} + 3} - \frac{a - 2}{a - 9}$ với a ≥ 0; a ≠ 9. Rút gọn B.

Đề bài. Cho biểu thức $P = \frac{3 x^{2} + 3 x}{(x + 1) (2 x - 6)}$ .

Đề bài. Cho biểu thức P = x³ + y³ – 3(x + y) + 1993. Tính giá trị biểu thức P với

$x = \sqrt[3]{9 + 4 \sqrt{5}} + \sqrt[3]{9 - 4 \sqrt{5}}; y = \sqrt[3]{3 - 2 \sqrt{2}} + \sqrt[3]{3 + 2 \sqrt{2}}$ .

Đề bài. Cho biểu thức: $Q = (\frac{1}{\sqrt{x} - 1} - \frac{1}{\sqrt{x}}) : (\frac{\sqrt{x} + 1}{\sqrt{x} - 2} - \frac{\sqrt{x} + 2}{\sqrt{x} - 1})$ .

Đề bài. Cho bốn số nguyên dương phân biệt sao cho tổng của mỗi hai số chia hết cho 2 và tổng của mỗi ba số chia hết cho 3. Tìm giá trị nhỏ nhất của tổng bốn số này?

Đề bài. Cho x ∈ ℕ nhưng x ∉ ℕ^* số x là:

Đề bài. Cho C = 1 + 3¹ + 3² + … + 3¹¹. Chứng minh rằng C ⋮ 13.

Đề bài. Cho hai góc kề bù $\hat{x O y}$ và $\hat{y O z}$ . Biết $\hat{x O y} = 50 °$ . Tính số đo góc $\hat{x O t}$ để tia Ot là tia phân giác của góc $\hat{y O z}$ .

Đề bài. Cho a, b, c là 3 số dương thỏa mãn ab + bc + ca = 3abc.

Đề bài. Cho các số nguyên a, b, c thỏa mãn điều kiện: (a – b)³ + (b – c)³ + (c – a)³ = 378. Tính giá trị của biểu thức .

Đề bài. Cho các số thực a, b, c thỏa mãn a + b + c = 0. Chứng minh rằng a⁵ + b⁵ + c⁵ chia hết cho 5.

Đề bài. Cho các số thực a, b, c thỏa mãn a² + b² + c² = 1.

Đề bài. Cho các số thực dương a, b, c thỏa mãn a + b + c = 3.

Đề bài. Cho các số thực x, y thỏa mãn 4x² + 2xy + y² = 3.

Đề bài. Cho các số thực x, y thỏa mãn x + y = 1, x³ + y³ = 2.

Đề bài. cho các tập hợp A = (2; +∞) và B =[m² - 7; +∞) với m > 0. Tìm m để A\B là một khoảng có độ dài bằng 16.

Đề bài. Cho D = 9 + 9² + 9³ + … + 9²⁰²⁰. Chứng tỏ D là bội của 41.

Đề bài. Cho đa thức P(x) với các hệ số nguyên thỏa mãn P(2021).P(2022) = 2023. Chứng minh rằng đa thức P(x) - 2024 không có nghiệm nguyên.

Đề bài. Cho dãy số: 2; 5; 8; 11; 14; … Tìm số thứ 100 của dãy số trên?

Đề bài. Cho dãy số: 2; 5; 8; 11; 14; … Tìm số thứ 2024 của dãy số trên?

Đề bài. Cho cấp số cộng (u_n) và gọi S_n là tổng n số hạng đầu tiên của nó. Biết S₇ = 77, S₁₂ = 192. Tìm số hạng tổng quát u_n của cấp số cộng đó?

Đề bài. Cho dãy số $u_{n} = \frac{1}{1.1!} + \frac{1}{2.2!} + \frac{1}{3.3!} + ... + \frac{1}{2013.2013!}$ . Chứng minh rằng $u_{n} < \frac{3}{2}$ .

Đề bài. Cho dãy số thập phân: 1,1; 2,2; 3,3; ......; 97,9; 99,0.

Đề bài. Cho dãy số 1,1; 2,2; 3,3; …; 108,9; 110,0

Đề bài. Cho điểm A và vectơ $\vec{a}$ khác 0. Tìm điểm M sao cho $\vec{A M}$ cùng phương với vectơ $\vec{a}$ .

Đề bài. Cho đường thẳng (d) có phương trình y = mx + 2. Tính m để khoảng cách từ gốc tọa độ O đến d là $\sqrt{2}$ .

Đề bài. Cho đường thẳng d song song với mặt phẳng (P). Mệnh đề nào sau đây đúng?

Đề bài. Cho đường tròn (O) đường kính AB. Vẽ đường tròn (I) đường kính OA. Bán kính OC của đường tròn (I) cắt đường tròn (I) tại O. Vẽ CH ⊥ AB. Chứng minh tứ giác ACDH là hình thang cân.

Đề bài. Cho đường tròn (O; R) có hai đường kính AB và CD vuông góc. Gọi I là điểm trên cung AC sao cho khi vẽ tiếp tuyến qua I và cắt DC kéo dài tại M thì IC = CM. Độ dài OM tính theo bán kính là?

Đề bài. Cho ba điểm A, B, C trên đường tròn (O). Tiếp tuyến tại A cắt dây cung CB kéo dài tại điểm M. Chứng minh: $\hat{M A C} = \hat{A B C} - \hat{A C B}$ .

Đề bài. Cho đường tròn tâm O. Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB, nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng:

Đề bài. Cho $0 < α < \frac{π}{2}$ . Khẳng định nào sau đây đúng?

Đề bài. Cho $\hat{B A C}$ = 70°, $\hat{A C B}$ = 55°, tia Ax là tia phân giác của $\hat{y A C}$ .

Đề bài. Cho góc nhọn xOy. Trên cạnh Ox lấy hai điểm A, B sao cho A nằm giữa O và B. Trên cạnh Oy lấy hai điểm C, D sao cho C nằm giữa O và D.

Đề bài. Cho góc $\hat{x O y} = 80 °$ Vẽ tia Oz là tia đối của tia Ox. Vẽ tia Om là tia phân giác của góc $\hat{z O y}$ .

Đề bài. cho hai đường thẳng a và b cắt đường thẳng c. Để có một cặp góc so le trong bằng nhau thì điều gì sau đây không thể xảy ra?

Đề bài. Cho hai đường tròn (O; R) và (O'; R') (R > R') tiếp xúc ngoài nhau tại A. Qua A kẻ hai cát tuyến BD và CE (B, C ∈ (O')); D, E ∈ (O)). Chứng minh: $\hat{A B C} = \hat{A D E}$ .

Đề bài. Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài tại A (R > R'). Vẽ các đường kính AOB, AO'C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC.

Đề bài. Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần lượt lấy các điểm M và N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M và N lần lượt cắt AD và AF tại M’ và N’. Chứng minh

Đề bài. Cho hai số thực a , b thỏa điều kiện ab = 1, a + b ≠ 0. Tính giá trị của biểu thức:

Đề bài. Cho hai tập hợp E = (2;5] và F = [2m - 3; 2m + 2]. Tìm tất cả các giá trị của tham số m để E hợp F là một đoạn có độ dài bằng 5.

Đề bài. Cho 2 tập hợp M = [2m − 1; 2m + 5] và N = [m + 1; m + 7] (với m là tham số thực). Tính tổng tất cả các giá trị của m để hợp của 2 tập hợp M và N là 1 đoạn có độ dài bằng 10.

Đề bài. Cho hàm số y = x – 2 có đồ thị là đường thẳng (d).

Đề bài. Cho hàm số f(x) hàm số y = f'(x) liên tục trên ℝ và có đồ thị như hình vẽ bên. Với giá trị nào của tham số m thì phương trình f(x) = 3x + m có nghiệm thuộc khoảng (-1;1).

Đề bài. Cho hàm số f(x) = ln(4x - x²). Tính đạo hàm của hàm số tại x = 2.

Đề bài. Xác định hàm số y = ax + b, biết đồ thị của hàm số đi qua hai điểm A(−2; 5) và B(1; −4).

Đề bài. Xác định các tham số a, b sao cho hàm số $y = \frac{a x + b}{x^{2} + 1}$ đạt GTLN = 4 và GTNN = -1.

Đề bài. Hàm số y = ∣x² − 2x − 3∣ đồng biến trên khoảng nào dưới đây?

Đề bài. Cho hàm số y = (m + 1)x + 3 (d) (m là tham số, m ≠ −1). Đường thẳng d cắt đường thẳng $y = - \frac{3}{2} x + 3 (d')$ tại điểm M. Gọi N và P lần lượt là giao điểm của đường thẳng (d) và (d′) với trục hoành Ox. Tìm m để diện tích tam giác OMP bằng 2 lần diện tích tam giác OMN.

Đề bài. Cho hàm số y= 2x³- 3(m + 1)x²+ 6mx + m³ với m là tham số thực. Tìm tất cả các giá trị của m để đồ thị hàm số có hai điểm cực trị A; B thỏa mãn $A B = \sqrt{2}$ .

Đề bài. Cho hàm số f(x) = 4x² − 4mx + m² − 2m + 2 (m là tham số). Gọi S là tập hợp tất cả các giá trị của m sao cho $\underset{[0; 2]}{M i n f (x)} = 3$ . Khẳng định nào đúng?

Đề bài. Cho hàm số bậc nhất y = (m – 2)x + 3. Tìm các giá trị của m để hàm số đồng biến.

Đề bài. Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới: Tìm tất cả các giá trị của tham số m để đồ thị hàm số $h (x) = |f^{2} (x) + f (x) + m|$ có đúng 3 điểm cực trị.

Đề bài. Cho hàm số y = f(x) có đồ thị như hình vẽ sau. So sánh f(3) và f(-2).

Đề bài. Cho hàm số: y = mx + 1 (1), trong đó m là tham số. Tìm m để đồ thị hàm số (1) đi qua điểm A(1; 4). Với giá trị m vừa tìm được, hàm số (1) đồng biến hay nghịch biến trên R?

Đề bài. Vẽ đồ thị của các hàm số y = x + 1 và y = -x +3 trên cùng một mặt phẳng tọa độ.

Đề bài. Cho hàm số $y = \frac{3 - x}{x + 1}$ . Hỏi mệnh đề nào sau đây đúng?

Đề bài. Cho phương trình x² – 5mx – 4m = 0 với m là tham số. Chứng minh rằng khi phương trình có 2 nghiệm phân biệt x₁, x₂ thì x₁² + 5mx₂ + m² + 14m + 1 > 0.

Đề bài. Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = -x³ + 3x² – 4. Nêu nhận xét về đồ thị của hàm số này.

Đề bài. Cho hàm số y = x² – x – 2. Khảo sát sự biến thiên và vẽ đồ thị hàm số (P) của hàm số.

Đề bài. Cho hình bình hành ABCD với AD = 2AB. Từ C vẽ CE vuông góc với AB. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE, MF cắt BC tại N.

Đề bài. Cho hình vẽ có MA // xy, NB // xy; $\hat{M A N} = 105 °$ .

Đề bài. Cho hình 20 biết a // AB, b // AB và $\hat{M A N} = 100 °$ . Tính $\hat{N_{1}}$ .

Đề bài. Cho Hình 21. Biết x // z, y // z và góc $\hat{C A D} = 120 °$ .

Đề bài. Cho hình vẽ biết AB // CD< AD // BC, AC cắt BD tại O. Chứng minh

Đề bài. Cho ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Gọi K là giao điểm của AC và DM, L là trung điểm cuả BD và CM.

Đề bài. Cho hình bình hành ABCD có $\hat{A} = 60 °$ , AB = 10cm, AD = 15cm. Tia phân giác của $\hat{A}$ cắt BC tại E.

Đề bài. Cho hình bình hành ABCD biết BD vuông góc với BC, AB = a, $\hat{A} = α$ . Tính S hình bình hành theo a và α?

Đề bài. Cho hình bình hành ABCD có $\hat{B A D} = 60 °$ ; AD = 2AB. Gọi M là trung điểm của BC, N là trung điểm của AD.

Đề bài. Cho hình bình hành ABCD. Gọi K, I lần lượt là trung điểm của AB và CD. Gọi M, N là giao điểm của AI, CK với BD. Chứng minh: ∆ADM = ∆CBN.

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, $\hat{B A C} = 60 °$ ; SO⊥(ABCD) và $S O = \frac{3 a}{4}$ . Tính thể tích khối chóp S.ABCD.

Đề bài. Cho hình chóp S.ABCD . Gọi M, N lần lượt là trung điểm của SB và SD. Thiết diện của hình chóp S.ABCD và mặt phẳng (AMN) là hình gì?

Đề bài. Cho chóp S.ABCD. M, N lần lượt là trung điểm của SB, SD. Tìm giao điểm của (AMN) và SC.

Đề bài. Cho hình chóp S.ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD.

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn BC = 2a đáy bé AD = a , AB = b. Mặt bên SAD là tam giác đều. M là một điểm di động trên AB, Mặt phẳng (P) đi qua M và song song với SA, BC.1. Tìm thiết diện của hình chóp khi cắt bởi mp (P). Thiết diện là hình gì?

Đề bài. Cho hình chóp S.ABCD. M là một điểm trên cạnh SC.

Đề bài. Cho hình chóp S.ABCD, AB và CD không song song và M là trung điểm của SC.

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

165

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

141

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.