Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 20)

Câu 31: Cho hình chữ nhật ABCD. Vẽ điểm E đối xứng với B qua điểm C; vẽ  F đối xứng với điểm D qua C.

a) Chứng minh tứ giác BDEF là hình thoi.

b) Chứng minh AC = DE.

c) Gọi H là trung điểm của CD, K là trung điểm của EF. Chứng minh HK // AF.

d) Biết diện tích tam giác AEF bằng 30 cm². Tính diện tích hình chữ nhật ABCD?

Lời giải:

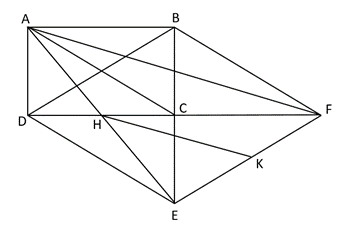
a) Xét tứ giác BDEF có:

C là trung điểm BF (E điểm đối xứng của B qua C)

C là trung điểm DF (F điểm đối xứng của D qua C)

Do đó tứ giác BDEF là hình bình hành

Mặc khác ABCD là hình chữ nhật nên BE ⊥ DF tại C

Vậy tứ giá BDEF là hình thoi.

b) Ta có: ABCD là hình chữ nhật có AC = BD;

BDEF là hình thoi (câu a) có BD = DE

Do đó AC = DE.

c) Ta có: ABCD là hình chữ nhật có AD = BC;

Mà BC = CE (E điểm đối xúng B qua C).

Do đó AD = CE.

Xét tứ giác ADEC có:

AC = DE (câu b)

AD = CE (cmt)

Do đó ADEC là hình hình hành.

Mà H là trung điểm cua CD nên H cũng là trung điểm của AE.

Xét ∆AEF có:

H là trng điểm của AE (cmt);

K là trung điểm của EF

⇒ HK là đường trung bình của ∆AEF nên HK // AF

d)  Ta có: S_∆AEF = S_∆AHF + S_∆HEF

$$\begin{gathered} \iff 30=\frac{1}{2}AD.HF+\frac{1}{2}CE.HF \\ \iff \frac{1}{2}HF\left(AD+CE\right)=30 \\ \iff \frac{1}{2}.\frac{3}{2}CD.\left(AD+AD\right)=30 \\ \iff \frac{3}{2}CD.AD=30 \\ \iff \frac{3}{2}.S_{ABCD}=30 \end{gathered}$$

$\Rightarrow S_{ABCD}=30.\frac{2}{3}=60$ (cm²).