Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Cho hàm số y = x2 và y = mx + 4, với m là tham số.
Bài 59: Cho hàm số y = x2 và y = mx + 4, với m là tham số.
a) Khi m = 3, tìm tọa độ các giao điểm của hai đồ thị hàm số trên.
b) Chứng minh rằng với mọi giá trị m, đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt A1(x1,y1);
A2 (x1 ,y2). Tìm tất cả các giá trị của m sao cho (y1)2 + (y2)2 = 72.
Lời giải:
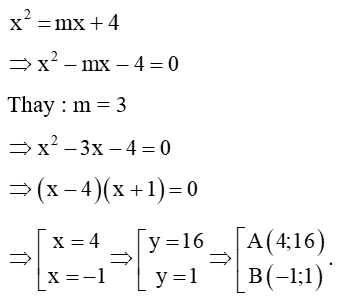
b) Ta có phương trình hoành độ giao điểm:
x2 – mx – 4 = 0.
Ta thấy ∆ = m2 + 16 > 0
Vậy phương trình luôn có hai nghiệm phân biệt x1 và x2.
Áp dụng định lí Vi – et, ta có:
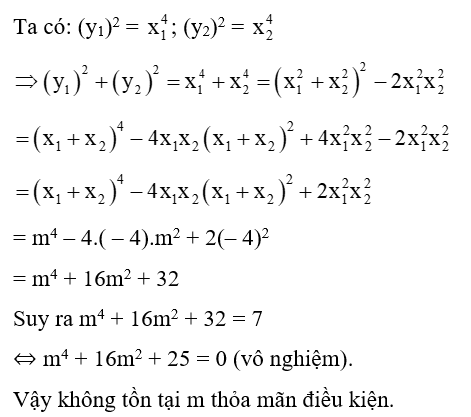
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Bài 4: Tìm giá trị nhỏ nhất, giá trị lớn nhất ...
Bài 6: cho các số hữu tỉ là a, b, c khác 0 thỏa mãn : . Tính giá trị của biểu thức ......
Bài 7: Cho biết và x + y + z =120 .Tìm x,y,....
Bài 8: Chứng minh đẳng thức...
Bài 9: Cho hai điểm A(x1; y1) và B(x2; y2) với . Chứng minh rằng nếu đường thẳng y = ax + b đi qua A và B thì ...
Bài 10: Cho hàm số y = -x + 5 có đồ thị là (d1)....
Bài 15: Cho vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.....
Bài 16: viết dưới dạng số thập phân là:...
Bài 18: Cho tam giác ABC có AB = AC và tia phân giác góc A cắt BC ở H....
Bài 19: Cho có AB = AC. Tia phân giác của góc A cắt BC tại D....
Bài 20: Cho hình vuông ABCD, M là trung điểm cạnh AB, P là giao điểm CM và DA...
Bài 22: Tính bằng cách thuận tiện nhất: 34 000 : 125 : 8 ...
Bài 24: Phân tích thành nhân tử 5(x + 3y) - 15x (x + 3y)....
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
