Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax, với đường tròn (O) (A là tiếp điểm)

Bài 41: Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax, với đường tròn (O) (A là tiếp điểm). Qua C thuộc tia

Ax, vẽ đường thẳng cắt đường tròn (O) tại hai điểm D và E (D nằm giữa C và E; D và E nằm về hai phía của đường

thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.

a) Chứng minh : tứ giác AOHC nội tiếp.

b) Chứng minh : AC . AE = AD . CE

c) Đường thẳng CO cắt tia BD, tia BE lần lượt tại M và N. Chứng minh : AM // BN

Lời giải:

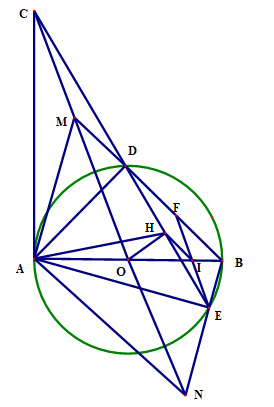
a) Ta có 

$\begin{array}{l}\stackrel{⏜}{\text{CAB}}{\text{ = 90}}^{\text{0}}\\ \stackrel{⏜}{\text{OHC}}{\text{ = 90}}^{\text{0}}\text{}\\ \Rightarrow \stackrel{⏜}{\text{CAB}}\text{ +}\stackrel{⏜}{\text{OHC}}{\text{ = 180}}^{\text{0}}\end{array}$

Vậy tứ giác AOHC nội tiếp.                                                   

b) Ta có $\stackrel{⏜}{\text{CAD}}\text{ = }\stackrel{⏜}{\text{AEC}}\text{, }\stackrel{⏜}{\text{ACE}}$ chung suy ra $\text{ΔACD ~ ΔECA}$ (g.g)

$\Rightarrow \frac{\text{CA}}{\text{CE}}\text{ = }\frac{\text{AD}}{\text{AE}}\Rightarrow \text{AC . AE = AD . CE}$

c) Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F

$\Rightarrow \stackrel{⏜}{\text{HEI}}\text{ = }\stackrel{⏜}{\text{HCO}}$

Vì tứ giác AOHC nội tiếp $\Rightarrow \stackrel{⏜}{\text{HAO}}\text{ = }\stackrel{⏜}{\text{HCO}}\text{ = }\stackrel{⏜}{\text{HEI}}$

Suy ra tứ giác AHIE nội tiếp $\Rightarrow \stackrel{⏜}{\text{IHE}}\text{ =}\stackrel{⏜}{\text{ IAE}}\text{ = }\stackrel{⏜}{\text{BDE}}\Rightarrow \text{HI // BD}$

Mà H là trung điểm của DE $\Rightarrow$  I là trung điểm của EF. Có EF // MN và IE =  IF

$\Rightarrow$ O là trung điểm của đoạn thẳng MN.

Suy ra tứ giác AMBN là hình bình hành $\Rightarrow$  AM//BN.