Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Cho tam giác ABC vuông tại A điểm M thuộc cạnh BC từ M vẽ các đường thẳng vuông góc

Bài 39: Cho $\Delta ABC$ vuông tại A điểm M thuộc cạnh BC từ M vẽ các đường thẳng vuông góc với AB ở D vuông góc

với AC ở E

a) cm AM = BE.

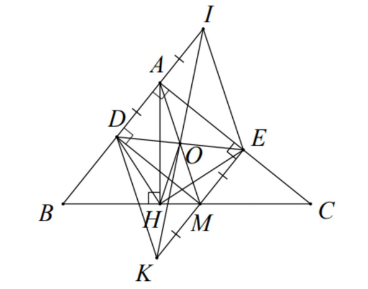
b) gọi l là điểm đx của D qua A và K là điểm đx của E qua M cm IK, DE, AM đồng quy hai trung điểm O của mỗi đoạn.

c) gọi AH là đường cao của tính số đo $\widehat{DHE}$ .

Lời giải:

a) Xét tứ giác ADME có $\widehat{\text{DAE}}\text{ =}\widehat{\text{ ADM}}\text{ = }\widehat{\text{AEM}}{\text{ = 90}}^{\text{o}}$

$\Rightarrow$ADME là hình chữ nhật

$\Rightarrow$AM= DE

b) Gọi O là giao điểm của AM và DE $\Rightarrow$  OA = OM = OD = OE (2)

Do ADME là hình chữ nhật $\Rightarrow$  DA = ME

$\Rightarrow$ 2DA = 2ME hay DA + AI = EM + MK (vì DA = AI; ME = MK)

$\Rightarrow$ DI = EK

Xét tứ giác DIEK có DI = EK (cmt)

     DI // EK (vì CEDM là HCN)

$\Rightarrow$ DKEI là hình bình hành

Do O là trung điểm của DE $\Rightarrow$  KI đi qua O

$\Rightarrow$ DE cắt IK tại O và OD = OE;  OK = OI (1) 

Từ (1) và (2) $\Rightarrow$  DE; AM; IK đồng quy tại trung điểm O của mỗi đường

c) Xét AHM vuông tại H có O là trung điểm của AM, khi đó HO là đường trung tuyến ứng với cạnh huyền AM. Suy ra $\text{HO = }\frac{\text{1}}{\text{2}}\text{ . AM}$

Mặt khác, AM = DE.

 $\Rightarrow \text{HO = }\frac{\text{1}}{\text{2}}\text{ . DE}$

Xét DHO có đường trung tuyến  $\text{HO = }\frac{\text{1}}{\text{2}}\text{ . DE}$

$\Rightarrow$ DHE vuông tại H  $\Rightarrow \widehat{\text{DHE}}{\text{ = 90}}^{\text{o}}$