Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 37)
Câu 10: Cho tam giác ABC cân tại A, đường trung tuyến CM và BN. Trên tia đối của tia BA lấy điểm D sao cho BD = AB. Chứng minh CD = 2CM.
Lời giải:
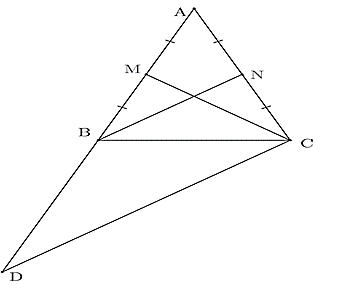
Gọi N là trung điểm cạnh AC. Suy ra BN là đường trung tuyến của ΔABC.
Vì ΔABC là tam giác cân tại A
Nên BN = CM. (1)
Xét tam giác ΔACD có B, N lần lượt là trung điểm cạnh AD và AC.
⇒ BN là đường trung bình của tam giác của ΔACD.
⇒ BN = DC ⇒ DC = 2BN. (2)
Từ (1) và (2) suy ra CD = 2CM.
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Câu 1: Tích 5 × 10 × 15 × 20 × 25 × 30 × ... × 100 có tận cùng bao nhiêu chữ số 0?..
Câu 2: Tính tổng các số tự nhiên nhỏ hơn 6....
Câu 3: Tính nhanh: 1.4 + 2.5 + 3.6 + ... + 100.103...
Câu 5: 16h40p là bao nhiêu giờ?..
Câu 11: Cho tam giác ABC có sin2 C = sin2 A + sin2 B. Tam giác ABC là tam giác gì? Vì sao?...
Câu 23: Chứng minh rằng: x5 – x + 2 không là số chính phương với mọi x thuộc Z...
Câu 24: Chứng minh 79m + 1 – 79m chia hết cho 78 (m thuộc ℕ)....
Câu 25: Kết quả chính xác của phép tính 264 + 1 là bao nnhiêu...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
