Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 37)
Câu 7: Cho hình bình hành ABCD. Gọi O là giao điểm của 2 đường chéo M, N là trung điểm của OD và OB. Gọi E là giao điểm của AM và CD. F là giao điểm của CN và AB.
a, Chứng minh: Tứ giác AMCN là hình bình hành
b, Tứ giác AECF là hình gì?
c, Chứng minh: E, F đối xứng qua O
d, Chứng minh: EC = 2DE.
Lời giải:
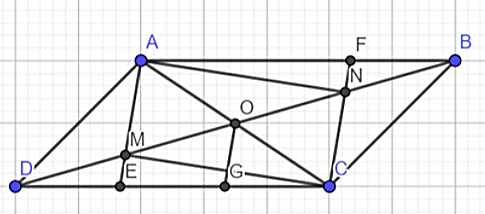
a,
Ta có ABCD là hình bình hành ⇒ AC ∩ BD tại trung điểm mỗi đường
Mà AC ∩ BD = 0 ⇒ O là trung điểm AC, DB
Lại có M, N là trung điểm OD, OB
⇒ OM = OD = OB = ON
⇒ O là trung điểm MN
Do O là trung điểm AC, MN
⇒ AMCN là hình bình hành (đpcm).
b,
Ta có AMCN là hình bình hành.
⇒ AM // CN
⇒ AE // CF
Mà AB // CD ⇒ AF // CE
⇒ AECF là hình bình hành.
c,
Ta có AECF là hình bình hành.
⇒ AC ∩ EF tại trung điểm mỗi đường
Mà O là trung điểm AC
⇒ O là trung điểm EF
⇒ E, F đối xứng nhau qua O (đpcm).
d,
Gọi G là trung điểm CE
Vì O là trung điểm AC ⇒ OG là đường trung bình ∆ACE
⇒ OG // AE
⇒ ME // OG
Mà M là trung điểm DO ⇒ ME là đường trung bình ∆ODG
⇒ E là trung điểm DG
⇒ DE = EG = GC
⇒ CE = CG + GE = DE + DE = 2DE (đpcm).
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Câu 1: Tích 5 × 10 × 15 × 20 × 25 × 30 × ... × 100 có tận cùng bao nhiêu chữ số 0?..
Câu 2: Tính tổng các số tự nhiên nhỏ hơn 6....
Câu 3: Tính nhanh: 1.4 + 2.5 + 3.6 + ... + 100.103...
Câu 4: 12m2 + 9dm2 = … dm2...
Câu 5: 16h40p là bao nhiêu giờ?..
Câu 6: Ba bạn Hùng Thắng Minh góp tiền ủng hộ người nghèo. Hùng góp 45000 đồng, Thắng góp 30000 đồng, Minh góp số tiền kém mức trung bình cộng của 3 bạn là 3000 nghìn. Hỏi Minh góp bao nhiêu tiền?...
Câu 7: Cho hình bình hành ABCD. Gọi O là giao điểm của 2 đường chéo M, N là trung điểm của OD và OB. Gọi E là giao điểm của AM và CD. F là giao điểm của CN và AB....
Câu 8: Cho hình thang vuông ABCD vuông tại A và B. Đáy nhỏ AD = a, BC = 3a, AB = 2a. I là trung điểm của AB. Tính BA + BC, DI + DC?...
Câu 9: Cho tam giác abc cân tại A có BD và CE là hai đường trung tuyến của tam giác. Chứng minh tứ giác BCDE là hình thang cân...
Câu 10: Cho tam giác ABC cân tại A, đường trung tuyến. CM và BN. Trên tia đối của tia BA lấy điểm D sao cho BD = AB. Chứng minh CD = 2CM....
Câu 11: Cho tam giác ABC có sin2 C = sin2 A + sin2 B. Tam giác ABC là tam giác gì? Vì sao?...
Câu 12: Cho nửa đường tròn tâm O có đường kính AB, C là một điểm thuộc nửa đường tròn, H là hình chiếu của C trên AB. Qua trung điểm M của CH, kẻ đường thẳng vuông góc với OC, cắt nửa đường tròn tại D và E. Chứng minh rằng AB là tiếp tuyến của đường tròn (C, CD).....
Câu 13: Tìm một số tự nhiên biết nếu xóa chữ số 3 ở hàng đơn vị của nó đi thì nó giảm đi 1794 đơn vị...
Câu 14: Có hai sợi dây sợi thứ nhất dài hơn sợi thứ hai 54m. Nếu cắt đi 1200 cm ở mỗi sợi thì phần còn lại của sợi thứ nhất gấp 4 lần phần còn lại của sợi thứ hai. Hỏi mỗi sợi dây dài bao nhiêu mét....
Câu 15: Đoạn thẳng AB dài 1km gồm hai đoạn thẳng AM và MB. Biết đoạn thẳng AM bằng đoạn thẳng MB. Tính độ dài đoạn thẳng MB....
Câu 16: Lớp 10A có 45 học sinh trong kì thi học kì 1 có 25 em đạt loại giỏi môn toán, 20 em đạt loại giỏi môn lý, 18 em đạt loại giỏi môn hoá. 6 em ko đạt loại giỏi bất kì môn nào, 5 em đạt loại giỏi 3 môn. Hỏi số học sinh chỉ đạt giỏi một môn và số học sinh giỏi hai môn?...
Câu 17: Có ba tổ trồng cây. Tổ 1 trồng được nhiều hơn trung bình cộng số cây của mỗi tổ là 6 cây. Tổ 2 trồng được số cây nhiều hơn trung bình cộng số cây của tổ 2 và tổ 3 là 1 cây. Biết tổ 3 trồng 26 cây. Hỏi tổ một trồng bao nhiêu cây?...
Câu 18: Có ba tổ tham gia trồng cây tổ 1 trồng được 1353 cây. Tổ 2 trồng được số cây bằng số cây của tổ 1. Tổ 3 trồng được số cây bằng số trung bình cộng của hai tổ đầu. Hỏi cả ba tổ trồng được bao nhiêu cây?...
Câu 19: Một bếp ăn dự trữ gạo đủ cho 120 người ăn trong 18 ngày. Nay có 80 người được chuyển đi nơi khác. Hỏi số gạo đó đủ cho những người còn lại ăn trong bao nhiêu ngày? (Mức ăn mỗi người như nhau)...
Câu 20: Một đội công nhân có 63 người nhận sửa xong một khối lượng quần áo trong 11 ngày. Hỏi muốn làm xong khối lượng quần áo đó trong 9 ngày thì cần thêm bao nhiêu người nữa? (Mức làm của mỗi người là như nhau)...
Câu 21: Một mặt hàng trước đây đã giảm 20% so với giá bán cũ. Hỏi mặt hàng đó cần phải tăng bao nhiêu phần trăm giá hiện đang bán để trở về giá bán ban đầu?...
Câu 22: Người ta mở rộng 1 thửa ruộng hình vuông theo cách sau: mở rộng lên phía trên 15m mở rộng phía dưới 10 mét thì được 1 hình chữ nhật có chu vi là 86 m. Tính diện tích thửa ruộng hình vuông?....
Câu 23: Chứng minh rằng: x5 – x + 2 không là số chính phương với mọi x thuộc Z...
Câu 24: Chứng minh 79m + 1 – 79m chia hết cho 78 (m thuộc ℕ)....
Câu 25: Kết quả chính xác của phép tính 264 + 1 là bao nnhiêu...
