Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 27)
Câu 28: Cho tam giác ABC cân tại A, đường cao AD, trực tâm H. Tính độ dài AD biết AH = 14 cm, BH = HC = 30 cm.
Lời giải:
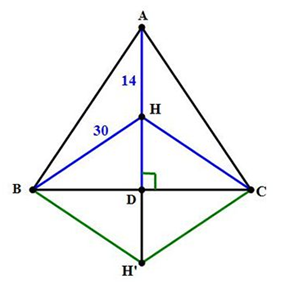
Gọi H’ là điểm đối xứng H qua BC.
Suy ra D là trung điểm của HH’
Vì tam giác ABC cân tại A, AD là đường cao nên AD là trung tuyến
Suy ra D là trung điểm của BC
Xét tứ giác BHCH’ có
D là trung điểm của HH’ và BC;
BC và HH’ là hai đường chéo
Suy ra BHCH’ là hình bình hành.
Mà BH = CH nên hình bình hành BHCH’ là hình thoi
Do đó BH’ // CH, BH = BH’.
Lại có CH ⊥ AB (vì H là trực tâm của tam giác ABC) nên BH’⊥ AB
Hay tam giác ABH’ vuông tại B
Mà BD ⊥ AH’
Suy ra H’B2 = H’D . H’A
⇔ HB2 = HD . (2HD + HA)
⇔ 302 = HD . (2HD + 14)
⇔ 2HD2 + 14HD – 900 = 0
⇔ (HD + 25)(HD – 18) = 0
⇔ HD – 18 = 0 (vì HD > 0)
⇔ HD = 18
Ta có AD = AH + HD = 14 + 18 = 32 cm
Vậy AD = 32 cm.
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Câu 5: Hình dưới đây có bao nhiêu hình tam giác, bao nhiêu hình tứ giác?...
Câu 12: Tìm tất cả giá trị thực của tham số m để tập hợp (1; m) chứa đúng hai số nguyên dương...
Câu 13: Xét sự đơn điệu của hàm số ...
Câu 17: Tính A = (x – 2)(x4 + 2x3 + 4x2 + 8x + 16) tại x = 3....
Câu 18: Cho các tập hợp A = (–2; 10), B = (m; m + 2). Tìm m để tập hơp A ∩ B là một khoảng:...
Câu 19: Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA...
Câu 22: Tìm x biết: sin2x + sin2 2x + sin2 3x = 2......
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
