Cho ∆ADC vuông tại a có đường cao AH, góc D = 65 độ , AH = 3 cm. Trên nửa mặt phẳng bờ DC chứa điểm A vẽ tia Cx song song

Cho ∆ADC vuông tại a có đường cao AH, góc D = 65 độ , AH = 3 cm. Trên nửa mặt phẳng bờ DC chứa điểm A vẽ tia Cx song song

Trịnh Thị Thu Hiền Ngày: 02-06-2023 Tổng hợp kiến thức

447

Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 14)

Câu 9: Cho ∆ADC vuông tại a có đường cao AH, $\hat{D} = 65 °$ , AH = 3 cm. Trên nửa mặt phẳng bờ DC chứa điểm A vẽ tia Cx song song với AD, trên Cx lấy điểm B sao cho CB = DA. Tính khoảng cách từ B đến AD, độ dài đoạn BD và diện tích tam giác ABD.

Lời giải:

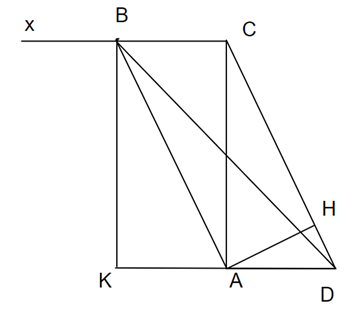
Tài liệu VietJack

Kẻ BK ⊥ AD

Xét ∆ADC $(\hat{A} = 90 °) : \hat{A D C} = 65 ° \Rightarrow \hat{A C D} = 25 °$

Khi đó: $C A = \frac{A H}{\sin \hat{C}} = \frac{3}{\sin 25 °}$

Dễ thấy BCAK là hình chữ nhật $\Rightarrow B K = A C = \frac{3}{\sin 25 °} (c m)$ và BC = AK

⟹ DA = AK (= BC) ⇒ DK = 2DA

Ta có: $D A = \frac{A H}{\sin \hat{C D A}} = \frac{3}{\sin 25 °} (c m)$

$D K = 2 D A = \frac{6}{\sin 25 °} (c m)$

Áp dụng định lí Pytago vào ∆BKD vuông tại K có $B K^{2} + K D^{2} = B D^{2}$

$\Leftrightarrow {(\frac{3}{\sin 25 °})}^{2} + {(\frac{6}{\sin 25 °})}^{2} = B D^{2} \Leftrightarrow B D^{2} = \frac{45}{\sin^{2} 25 °} \Leftrightarrow B D = \frac{3 \sqrt{5}}{\sin 25 °} (c m)$

Ta có

$S_{A B D} = S_{B K D} - S_{B A K} = \frac{B K . K D}{2} - \frac{A K . B K}{2} = \frac{B K}{2} (K D - A K) = \frac{B K . A D}{2} = \frac{\frac{3}{\sin 25 °} . \frac{3}{\sin 25 °}}{2} = \frac{18}{\sin 25 °} (c m^{2})$

Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:

Câu 1: Cho ∆ABC đều, cạnh AB = BC = AC = a = 6, kẻ đường cao từ A xuống cắt với BC tại H, tính chiều cao AH....

Câu 2: Cho biểu thức $P = (\frac{x - 3 \sqrt{x}}{x - 9} - 1) : (\frac{9 - x}{x + \sqrt{x} - 6} - \frac{\sqrt{x} - 3}{2 - \sqrt{x}} - \frac{\sqrt{x} - 2}{\sqrt{x} + 3})$ . Tìm giá trị của x để P < 1....

Câu 3: Tìm x biết: x + 12 = – 5 – x....

Câu 4: Cho $\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$ và $\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0$ . Chứng minh rằng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} + \frac{z^{2}}{c^{2}} = 1$ ....

Câu 5: Cho hàm số $y = \frac{2 x + 7}{x + 2}$ có đồ thị (C). Hãy chọn mệnh đề sai:..

Câu 6: Cho α là góc tù và sinα – cosα = $\frac{4}{5}$ . Giá trị của M = sinα – 2cosα là ?..

Câu 7: Giải phương trình: $\sqrt{4 x^{2} + 5 x + 1} - 2 \sqrt{x^{2} - x + 1} = 9 x - 3$ ...

Câu 8: Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng $a \sqrt{2}$ . Tính thể tích của khối chóp S.ABC ?..

Câu 9: Cho ∆ADC vuông tại a có đường cao AH, $\hat{D} = 65 °$ , AH = 3 cm. Trên nửa mặt phẳng bờ DC chứa điểm A vẽ tia Cx song song với AD, trên Cx lấy điểm B sao cho CB = DA. Tính khoảng cách từ B đến AD, độ dài đoạn BD và diện tích tam giác ABD....

Câu 10: Tính thể tích V của khối chóp tam giác đều S.ABC, biết chiều cao hình chóp bằng h, $\hat{S B A} = α$ ...

Câu 11: Cho hình chóp tứ giác đều S.ABCD có chiều cao h, góc ở đỉnh của mặt bên bằng 60°. Tính thể tích hình chóp...

Câu 12: Giả sử x và y là các biến số. Hãy cho biết kết quả của việc thực hiện thuật toán sau:...

Câu 13: Viết chương trình nhập số nguyên dương n. Kiểm tra n có phải là số nguyên tố hay không ?..

Câu 14: Cho 2 điểm A(3; 0), B(0; 4). Phương trình đường tròn (C) có bán kính nhỏ nhất nội tiếp ∆OAB là ?...

Câu 15: Giải phương trình: $(x^{2} - 5 x + 1) (x^{2} - 4) = 6 {(x - 1)}^{2}$ ....

Câu 16: Cho các số từ 1 đến 9. Hãy điền các số này vào các ô vuông, sao cho tổng của 3 ô hàng dọc, hàng ngang và đường chéo đều bằng nhau....

Câu 17: Vẽ bản đồ tư duy hình vuông....

Câu 18: Vẽ bản đồ tư duy hình chữ nhật..

Câu 19: Tìm các số nguyên x, y thỏa mãn: $5 x^{2} - 4 x y + y^{2} = 169$ ....

Câu 20: Cho ∆ABC, tìm vị trí điểm I sao cho $2 \vec{I A} - 3 \vec{I B} - \vec{I C} = \vec{0}$ ...

Câu 21: Một thùng đựng 39,75 kg đường, người ta lấy ra 10,5 kg rồi lại lấy tiếp 5 kg đường nữa. Số đường trong thùng còn lại là ?....

Câu 22: Một cửa hàng ngày thứ nhất bán được 35,5 mét vải, ngày thứ hai bán gấp đôi ngày thứ nhất và kém ngày thứ ba 3 mét. Hỏi cả ba ngày cửa hàng đó bán được bao nhiêu mét vải ?....

Câu 23: Hoàn thiện chương trình dưới đây, chương trình nhập từ bàn phím 3 số thực a, b, c đưa ra thông điệp “Cả 3 số đều dương” nếu cả 3 số đều dương....

Câu 24: Một của hàng bán vật liệu xây dựng có 127,5 tạ xi măng. Buổi sáng cửa hàng bán được $\frac{1}{5}$ lượng xi măng đó, buổi chiều bán được $\frac{1}{5}$ lượng xi măng còn lại. Hỏi cả sáng và chiều của hàng đó bán được bao nhiêu tạ xi măng ?...

Câu 25: Đổi 123 phút = .......... giờ ...........phút ?....

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

166

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

141

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.