Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 8)

Câu 19: Giải phương trình lượng giác: 2sinx.(1 + cos2x) + sin2x = 1 + 2cosx

Lời giải:

2sinx(1 + cos2x) + sin2x = 1 + 2cosx

⇔ 2sinx.(1 + 2cos²x – 1) + 2sinxcosx = 1 + 2cosx

⇔ 2sinx.2cos²x + 2sinxcosx = 1 + 2cosx

⇔ 2sinxcosx(2cosx + 1) = 1 + 2cosx

⇔ 2sinxcosx(2cosx + 1) – (1 + 2cosx) = 0

⇔ (2cosx + 1)(2sinxcosx – 1) = 0

⇔ (2cosx + 1).(sin2x – 1) = 0

$\iff \left[\begin{array}{l}2\cos x+1=0\\ \sin 2x-1=0\end{array}\right.\iff \left[\begin{array}{l}\cos x=\frac{-1}{2}\\ \sin 2x=1\end{array}\right.\iff \left[\begin{array}{l}\left\{\begin{array}{l}x=\frac{2\pi }{3}+k2\pi \\ x=-\frac{2\pi }{3}+k2\pi \end{array}\right.\\ 2x=\frac{\pi }{2}+k2\pi \end{array}\right.(k\in \mathbb{Z})$

$\iff \left[\begin{array}{l}\left\{\begin{array}{l}x=\frac{2\pi }{3}+k2\pi \\ x=-\frac{2\pi }{3}+k2\pi \end{array}\right.\\ x=\frac{\pi }{4}+k\pi \end{array}\right.(k\in \mathbb{Z})$

Phương pháp giải

- Phương trình sinx = a        (1)

    ♦ |a| > 1: phương trình (1) vô nghiệm.

    ♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.

Khi đó phương trình (1) có các nghiệm là

                x = α + k2π, k ∈ Z

                và x = π-α + k2π, k ∈ Z.

Nếu α thỏa mãn điều kiện 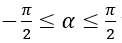 và sinα = a thì ta viết α = arcsin a.

Khi đó các nghiệm của phương trình (1) là

                x = arcsina + k2π, k ∈ Z

                và x = π - arcsina + k2π, k ∈ Z.

Các trường hợp đặc biệt:

- Phương trình cosx = a        (2)

    ♦ |a| > 1: phương trình (2) vô nghiệm.

    ♦ |a| ≤ 1: gọi α là một cung thỏa mãn cosα = a.

Khi đó phương trình (2) có các nghiệm là

                x = α + k2π, k ∈ Z

                và x = -α + k2π, k ∈ Z.

Nếu α thỏa mãn điều kiện 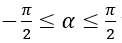 và cosα = a thì ta viết α = arccos a.

Khi đó các nghiệm của phương trình (2) là

                x = arccosa + k2π, k ∈ Z

                và x = -arccosa + k2π, k ∈ Z.

Các trường hợp đặc biệt: