Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 13)
Câu 15: Cho tam giác ABC vuông tại A có AB = AC. Qua A kẻ đường thẳng d (B, C nằm cùng phía đối với d). Kẻ BM và CN vuông góc với d. Chứng minh rằng:
a) ∆BAM = ∆CAN.
b) MN = BM + CN.
Lời giải:
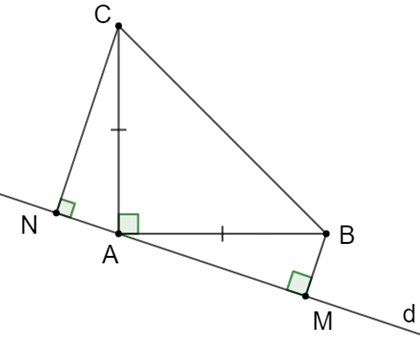
a) Xét tam giác ACN vuông tại N
(1)
Mà (2)
Từ (1) và (2) suy ra (hai góc cùng phụ với )
Xét ∆NCA và ∆MAB vuông tại N và M có:
(cmt)
AC = BA (gt)
=> ∆NCA = ∆MAB (cạnh huyền – góc nhọn)
Vậy ∆BAM = ∆CAN (đpcm).
b) ∆NCA = ∆MAB => BM = AN và CN = AM (các cặp cạnh tương ứng bằng nhau)
=> MN = MA + AN = CN + BM
Vậy MN = BM + CN (đpcm)
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Câu 3: Cho tan a + cot a = m. Tìm m để tan2 a + cot2 a = 7.....
Câu 4: Cho tan a + cot a = m. Tính tan3 a + cot3 a theo m...
Câu 6: Cho biểu thức . Tìm x để ....
Câu 10: Chứng minh bất đẳng thức: a2 + b2 + c2 ≥ ab + bc + ca....
Câu 11: Cho a2 + b2 + c2 = ab + bc + ca. Chứng minh a = b = c...
Câu 16: Số nghiệm của phương trình cos 2x + 3sin x − 2 = 0 trên khoảng (0; 20π) là bao nhiêu?...
Câu 17: Giải phương trình: cos 2x + 3sin x − 2 = 0....
Câu 18: Tính sin x, cos x, tan x, cot x biết ....
Câu 19: Cho . Hãy tính: A = sin x.cos x....
Câu 24: A \ B được gọi là phần bù của B trong A khi nào?....
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
