Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Cho ΔABC, gọi I là giao điểm 3 đường phân giác trong
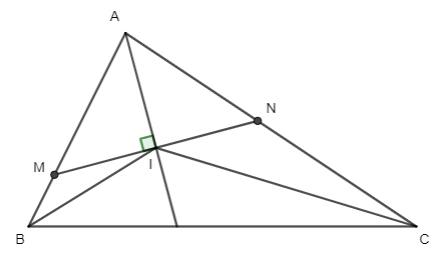
Bài 19: Cho ΔABC, gọi I là giao điểm 3 đường phân giác trong. Qua I vẽ đường thẳng vuông góc AI cắt AB, AC tại
M, N. Chứng minh rằng:
a)
b) BM.AC + CN.AB + AI2 = AB.AC
Lời giải:
a) Xét tam giác AIM vuông tại I có:
Xét tam giác BIC, có:
Xét ∆BMI và ∆BIC, có:
(cmt)
⇒ ∆BMI ̴ ∆BIC (g – g)
Chứng minh tương tự ta có ∆CNI ̴ ∆CIB (g – g)
.
b) Từ cm trên suy ra :△BMI ∼ △INC
⇒ BM.CN = MI.NI
ta có : △AMN là tam giác cân
⇒ MI = NI
⇒ BM.CN = IM2
ta lại có : △AIM vuông
⇒ IM2 = AM2 – AI2
⇒ BM.CN = AM2 – AI2
= AM.AN – AI2 = (AB − BM)(AC − CN) – AI2
= AB.AC − AB.CN − BM.AC + BM.CN – AI2
⇒ BM.AC + CN.AB + AI2 = AB.AC.
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Bài 1. Cho tam giác ABC, M, N, P được xác định bởi véctơ...
Bài 2. Cho a,b ≠ -2 thỏa mãn (2a + 1)(2b + 1) = 9...
Bài 3. Chứng minh các bất đẳng thức: với a > 0, b > 0...
Bài 4. Cho a > 0 và b > 0. Chứng minh rằng ...
Bài 10. Cho Tính giá trị của biểu thức ...
Bài 11. Cho a, b, c khác nhau đôi một và . Rút gọn biểu thức:...
Bài 17: Nếu đặt mặt đáy của hình nón song song với mặt phẳng chiếu cạnh thì hình chiếu đứng và hình chiếu cạnh có hình dạng:...
Bài 19: Cho ΔABC, gọi I là giao điểm 3 đường phân giác trong. Qua I vẽ đường thẳng vuông góc AI cắt AB, AC tại M, N. Chứng minh rằng:...
Bài 21: Tìm tất cả các giá trị của tham số m để khoảng cách từ điểm A (−1; 2) đến đường thẳng Δ: mx + y – m + 4 = 0 bằng ...
Bài 22: Tìm tất cả các giá trị thực của tham số m để hàm số có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O...
Bài 23: Có tam giác ABC vuông tại A đg cao AH, E, F lần lượt là hình chiếu của H lên AB, AC. CM: BE.AC + CF. AB = AH. BC...
Bài 24: Cho tam giác ABC vuông tại A có AB = 3 cm; AC = 4 cm, đường cao AH. Gọi E, F lần lượt là hình chiếu của H lên AB, AC. Chứng minh rằng: AE. AB = AF. AC...
Bài 25: Cho biết x và y là hai đại lượng tỉ lệ nghịch và khi x = 9 thì y = - 15...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
