Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 49)
Câu 7: Cho hình chữ nhật ABCD (AB > BC). Từ B kẻ BH vuông góc với AC tại H. Lấy E sao cho H là trung điểm BE, lấy Q đối xứng với C qua H. QE cắt DC tại M. Gọi N là hình chiếu của E trên AD, MN cắt DE tại O. Chứng minh tam giác OEM là tam giác cân.
Lời giải:
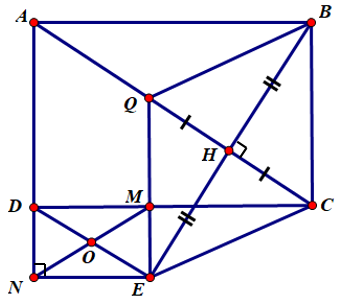
Ta có: NE ⊥ AD; DM ⊥ AD
⇒ DM // NE
Xét tứ giác BCEQ có:
BE ⊥ QC = {H}
H là trung điểm của QC
H là trung điểm của BE
⇒ BCEQ là hình thoi
⇒ BC // QE
Mà BC // AD
Nên QE // AD
Xét tứ giác DMEN có:
DM // NE
QE // DN
⇒ DMEN là hình bình hành
Mà
⇒ DMEN là hình chữ nhật
⇒ OM = OE.
Vậy tam giác OME cân tại O.
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Câu 1: Tìm x, biết: x(x − 3) + 5x = x2 – 8........
Câu 2: Có bao nhiêu số tự nhiên có 3 chữ số dôi một khác nhau?......
Câu 16: Tính tổng của dãy số lẻ từ 11 đến 99.....
Câu 17: Tính tổng của dãy số chẵn từ 10 đến 50.....
Câu 21: Giá trị lớn nhất của biểu thức A = 125 × a − b × 25 với a, b là các số có hai chữ số.......
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
