Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 31)
Câu 32: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là các tiếp điểm). Chứng minh rằng OAMN.
Lời giải:
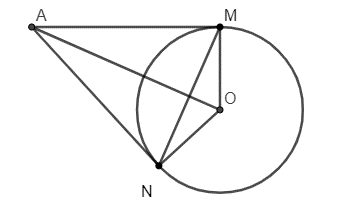
Ta có: AM = AN (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AMN cân tại A
Mặt khác AO là đường phân giác của (tính chất hai tiếp tuyến cắt nhau)
Suy ra AO là đường cao của tam giác AMN (tính chất tam giác cân)
Vậy OA ⊥ MN.
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Câu 1: Giải phương trình: x5 + x4 – x3 + x2 – x + 2 = 0.....
Câu 3: Giải phương trình: x . 3,9 + x . 0,1 = 2,7....
Câu 5: Tìm các số tự nhiên x sao cho: x ⋮ 15 và 0 < x < 40...
Câu 9: Thu gọn: S = 1 + x + x2 + x..3 + …. + xn...
Câu 11: Cho biết 3 người làm cỏ một cánh đồng hết 6 giờ. Hỏi 12 người (có cùng năng suất) làm cỏ cánh đồng đó hết bao nhiêu thời gian?..
Câu 12: 7a + 4b = 26. Tìm a và b....
Câu 13: Cho a, b > 0 thỏa mãn: a + b = 4. Tìm GTNN của: .....
Câu 17: Giải phương trình: y : 15 – 34,87 = 52,21 + 6....
Câu 20: Bạn Mai dùng 25 000 đồn.g mua bút. Có hai loại bút: Loại I giá 2000 đồng một chiếc, loại II giá 1500 đồng một chiếc. Bạn Mai mua được nhiều nhất bao nhiêu chiếc bút nếu:...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
