Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 12)
Câu 38: Cho hình bình hành ABCD. Gọi d là đường thẳng qua A và không cắt đoạn thẳng BD. Gọi BB’, CC’, DD’ lần lượt là khoảng cách từ B, C, D đến đường thẳng d (B’, C’, D’ ∈ (d)). Chứng minh rằng BB’ + DD’ = CC’.
Lời giải:
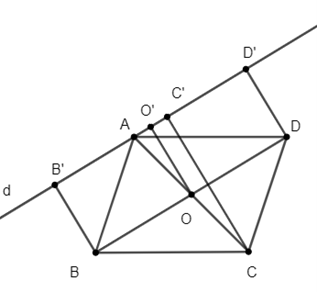
Gọi O là giao điểm của AC và BD. ABCD là hình bình hành nên O là trung điểm của AC và BD. Vẽ OO’⊥ d, O’ ∈ d.
Các đường thẳng BB’, CC’, DD’, OO’ song song với nhau (vì cùng vuông góc với đường thẳng d).
Vì B’D’DB là hình thang (vì BB’ // DD) có OB = OD, OO’ // BB’ nên OO’ là đường trung bình của hình thang B’D’DB.
Do đó .
Mặt khác ∆ACC’ có OO’ // CC’ và OA = OC.
Nên OO’ là đường trung bình của tam giác ACC’, suy ra: .
Từ (1) và (2) suy ra BB’ + DD’ = CC’.
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Câu 2: Tìm ƯCLN và tập hợp ước chung của các số sau:...
Câu 3: Tìm điều kiện của a và b để M xác định và rút gọn M:......
Câu 4: Tìm điều kiện để a, b để A = [a; a + 1] giao B = [b – 1; b + 2] khác rỗng....
Câu 6: Cho hàm số y = (m – 1)x + m....
Câu 8: Tìm tọa độ điểm D sao cho ABCD là hình bình hành biết A(4; 3), B(−1; 2), C(1; −1)....
Câu 10: Chứng minh rằng với mọi số thực a, b ta luôn có: a2 + b2 ≥ 2ab...
Câu 11: a) Chứng minh rằng a2 + ab + b2 ≥ 0 với mọi số thực a, b....
Câu 12: Rút gọn biểu thức: ...
Câu 13: Đổi một số đơn vị sau:...
Câu 16: Số điểm biểu diễn của nghiệm của phương trình trên đường tròn lượng giác là..
Câu 17: Trên đường tròn lượng giác số điểm biểu diễn tập nghiệm của phương trình là...
Câu 18: Tính chu vi tam giác ABC biết AB = 6 và 2sinA = 3sinB = 4sinC...
Câu 19: Phân tích đa thức thành nhân tử:..
Câu 20: Tính giá trị của biểu thức: x(x – 1) – y(1 – x) tại x = 2001 và y = 1999....
Câu 21: Cho hàm số y = (2m – 1)x – m + 2. Tìm m để đồ thị hàm số đi qua A(1; 2):..
Câu 22: Cho hàm số y = (2 + m)x – 4...
Câu 23: Cho tam giác ABC có ; . Chứng minh tam giác ABC cân.....
Câu 25: Cho hình thang ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA.....
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
