Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD
Bài 20: Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD
a) Các tứ giác AEFD, AECF là hình gì? Vì sao?
Lời giải:
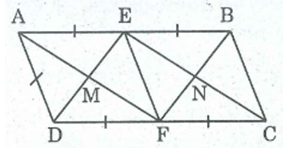
a) Ta có: và AE // DF
→ tứ giác AEFD là hình bình hành
Có thêm
→AEFD là hình thoi (dấu hiệu nhận biết hình thoi)
AE // FC và AE = FC ( vì cùng )
→ AECF là hình bình hành
b) Tứ giác AECF là hình bình hành nên EN // MF(1)
Chứng minh tương tự câu a tứ giác EBFN là hình bình hành
→ ME // FN(2)
Từ (1) và (2) suy ra EMFN là hình bình hành (3)
Tứ giác AEFD là hình thoi nên suy ra
(4)
Từ (3) và (4) suy ra EMFN là hình chữ nhật
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Bài 1: Hai góc tương ứng là gì?...
Bài 3: Có bao nhiêu phân số thập phân có tử số là 3, lớn hơn và nhỏ hơn ....
Bài 7: Xác định 4 góc của một tứ giác lồi, biết rằng đo 4 góc lập thành 1 cấp số cộng và góc lớn nhất bằng 5 lần góc nhỏ nhất ?...
Bài 8: Hiện nay bố 32 tuổi, con 5 tuổi. Hỏi mấy năm nữa thì tuổi bố gấp 4 lần tuổi con?...
Bài 9: Tìm số thực a biết: chia x – 2 dư 3...
Bài 14: Cho tam giác ABC có trọng tâm G. Khi đó...
Bài 17: Tính tổng T các nghiệm của phương trình sin2x – cosx = 0 trên ..
Bài 18: Thực hiện các phép tính...
Bài 20: Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD...
Bài 21: Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có BC = 3, góc . Tính...
Bài 25: Tìm ảnh của đường tròn (C): qua phép quay Q( I; 90°) với I(3; 4)....
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
