Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 51)
Câu 21: Cho ∆ABC có 3 góc nhọn, AH là đường cao. Vẽ HE vuông góc với AB tại E, HF vuông góc AC tại F .
a) Chứng minh: AE.AB = AF.AC.
b) Cho BH = 3cm, AH = 4cm. Tính AE, BE.
Lời giải:
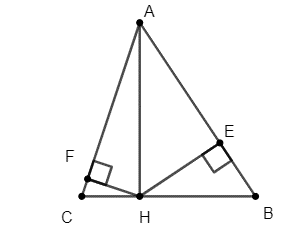
a) Xét ΔAHB vuông tại H, HE là đường cao nên ta có AH² = AE.AB
Xét ΔAHC vuông tại H, HF là đường cao nên ta có AH² = AF.AC
⇒ AE.AB = AF.AC
b) Xét ΔAHB vuông tại H. Áp dụng định lý Py-ta-go:
AB² = AH² + BH² = 16 + 9 = 25
⇒ AB = 5 (cm)
Có AH² = AE.AB ⇒ AE = 3,2 (cm)
Có BE = AB – AE = 5 – 3,2 = 1,8 (cm)
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Câu 1: Cho f(x) = −x2 − 2(m − 1)x + 2m − 1...
Câu 5: Cho B=3 + 32 + 33 + ... + 3120. Chứng minh:....
Câu 6: Cho B = 3 + 32 + 33 + ... + 3120. Chứng minh B chia hết cho 13....
Câu 7: Chứng minh rằng biểu thức:......
Câu 8: Chứng minh 4x − 10 − x2 luôn luôn âm với mọi x.....
Câu 9: Tìm GTNN của B = 2x2 + 3y2 + 4xy − 8x − 2y + 1....
Câu 10: Có bao nhiêu số tự nhiên gồm 5 chữ số phân biệt sao cho 1,2,3 luôn đứng cạnh nhau.....
Câu 11: Có bao nhiêu số tự nhiên có 3 chữ số khác nhau mà tổng các chữ số là chẵn?........
Câu 13: Xét vị trí tương đối của hai đường thẳng d1: x − 2y + 1 = 0 và d2: −3x + 6y – 10 = 0.......
Câu 14: Cho đoạn thẳng AB. Xác định vị trí của điểm C trên đoạn thẳng AB sao cho CA ≤ CB......
Câu 16: Giải phương trình: 2x + 1 − 2x = 32......
Câu 17: Giải phương trình: 22x + 1 = 32.......
Câu 18: Thu gọn biểu thức sau: A = 1 – 3 + 32 – 33 + … + 32021 – 32022..........
Câu 19: Tính giá trị của biểu thức: P = 1 + 2 + 22 + 23 + 24 + … + 22020......
Câu 20: Tính tổng của tất cả số tự nhiên x, biết x là số có 2 chữ số và 12 < x < 91........
Câu 22: Chứng minh rằng n4 + 2n3 – n2 – 2n chia hết cho 24 với mọi số nguyên n......
Câu 23: Có bao nhiêu số nguyên dương không vượt quá 1000 mà chia hết cho 3 hoặc chia hết cho 5......
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
