Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 32)
Câu 18: Cho tam giác ABC. Gọi H là trực tam của tam giác. Chứng minh rằng: AH2 + BC2 = BH2 + AC2
Lời giải:
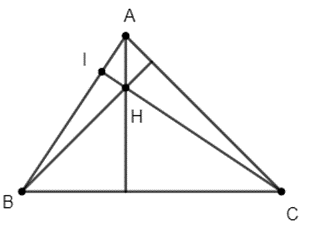
Gọi I là giao điểm của CH và AB.
Áp dụng định lý Py-ta-go cho các tam giác vuông ∆AHI, ∆BHI, ∆ACI, ∆BCI ta có:
AH2 = AI2 + HI2 ⇒ AH2 – AI2 = HI2
BH2 = IH2 + BI2 ⇒ BH2 – BI2 = IH2
AC2 = AI2 + IC2 ⇒ AC2 – AI2 = IC2
BC2 = BI2 + IC2 ⇒ BC2 – BI2 = IC2
Suy ra:
AH2 – AI2 = BH2 – BI2 (1)
AC2 – AI2 = BC2 – BI2 (2)
Trừ (2) cho (1) ta được:
AC2 – AH2 = BC2 – BH2
⇒ AH2 + BC2 = BH2 + AC2 (đpcm)
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Câu 1: Tính tổng: A = 1 + 3 + 5 + 7 + … + (2n – 1)....
Câu 2: Số 46 có phải số chính phương không?...
Câu 3: Với mọi số tự nhiên n thì an = n(n + 1)(n + 2)(n + 3) + 1 là số chính phương....
Câu 5: Cho dãy số 4; 7; 10; 13; 16;......
Câu 6: Hãy cho biết có tất cả bao nhiêu số tự nhiên có 2 chữ số nhỏ hơn 68?...
Câu 7: Có 15 công nhân dự định làm công việc trong 20 ngày. Sau khi làm được 6 ngày có 5 người phải chuyển đi nơi khác. Hỏi họ cần mấy ngày nữa để làm xong công việc đó?....
Câu 8: Một kho chứa 672 bao, mỗi bao chứa 50 kg thóc.Người ta lấy đi.....
Câu 10: Kết quả của phép chia: (6xy2 + 4x2y – 2x3) : 2x là:..
Câu 11: Rút gọn biểu thức: Q = (2x + 3y)(4x2 – 6xy + 9y2)...
Câu 13: Xếp các số thập phân sau theo thứ tự từ bé đến lớn: 8,09; 8,9; 8,89; 8,8...
Câu 14: Số hạng tiếp theo của dãy số:...
Câu 15: Phân tích đa thức thành nhân tử: x4 + 6x3 + 7x2 – 6x + 1....
Câu 16: Rút gọn biểu thức: P = 12.(52 + 1)(54 + 1)(58 + 1)(516 + 1)....
Câu 17: Chứng minh rằng: 35x – 14y + 29 – 1 chia hết cho 7...
Câu 18: Cho tam giác ABC. Gọi H là trực tam của tam giác. Chứng minh rằng: AH2 + BC2 = BH2 + AC2....
Câu 19: Cho f(x) = ax3 + 4x(x2 – x) – 4x + 8; g(x) = x3 – 4x(bx + 1) + c – 3...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
