Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 73)
Câu 34: Cho tam giác ABC cân tại A, đường cao CD. Chứng minh rằng:
AB2 + BC2 + AC2 = BD2 + 2AD2 + 3CD2.
Lời giải:
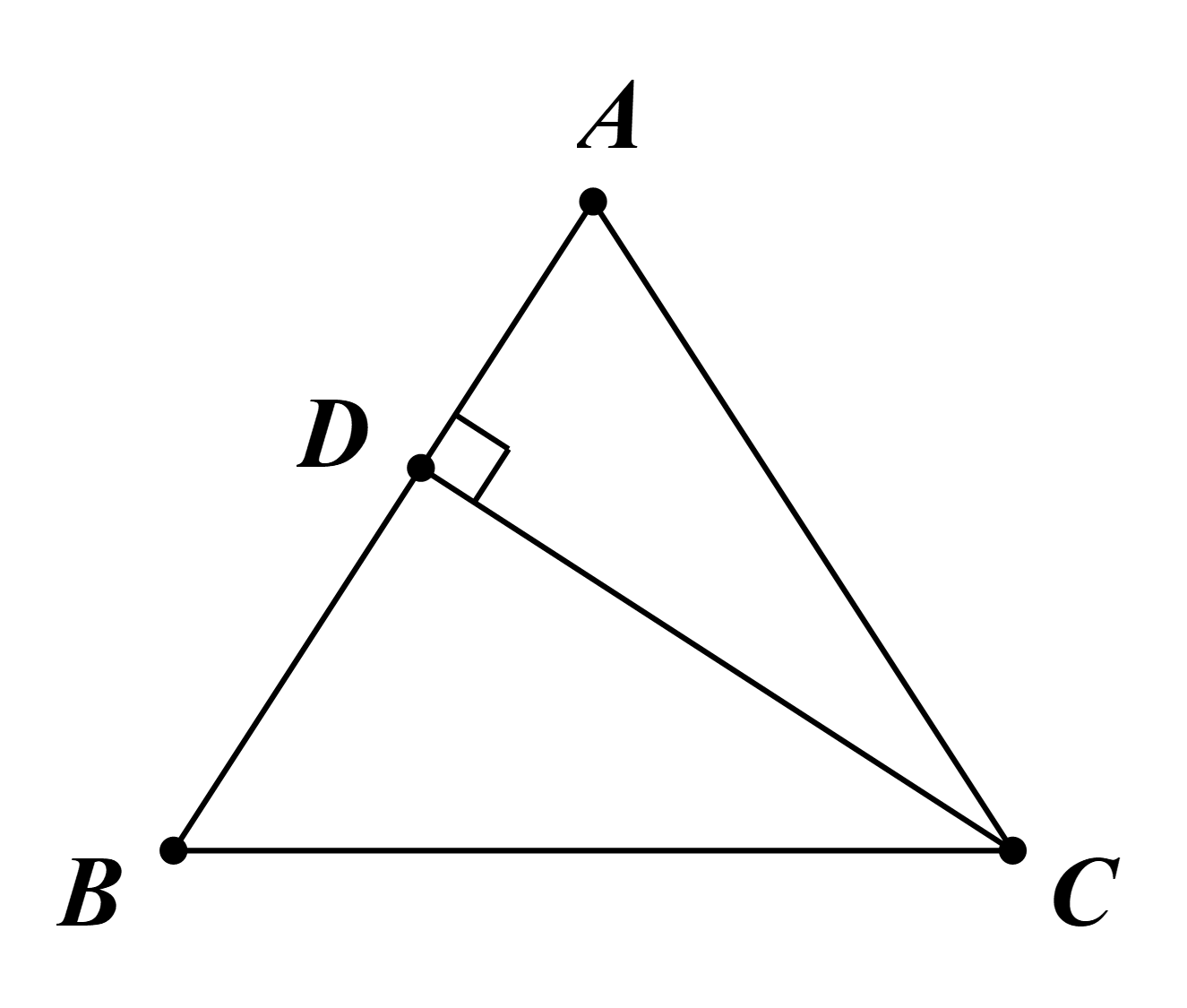
Áp dụng định lí Pytago cho tam giác ACD vuông tại D: AD2 + CD2 = AC2 (1)
⇔ AD2 + CD2 = AB2 (do tam giác ABC cân tại A nên AB = AC) (2)
Áp dụng định lí Pytago cho tam giác DBC vuông tại D: BD2 + CD2 = BC2 (3)
Lấy (1) + (2) + (3) vế theo vế, ta được: BD2 + 2AD2 + 3CD2 = AB2 + BC2 + AC2.
Vậy ta có điều phải chứng minh.
Xem thêm các nội dung khác:






