Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 69)

Câu 11:  Một công ty cần thuê xe để chở 120 người và 6,5 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 9 chiếc và loại xe B có 8 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi chiếc xe loại A có thể chở tối đa 20 người và 0,5 tấn hàng; mỗi chiếc xe loại B có thể chở tối đa 10 người và 2 tấn hàng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí bỏ ra là thấp nhất?

Lời giải:

Gọi số xe loại A cần thuê là: x (chiếc) (x ∈ ℕ);

Số xe loại B cần thuê là: y (chiếc) (y ∈ ℕ)

Xe loại A có 9 chiếc, xe loại B có 8 chiếc 

⇒ 0 ≤ x ≤ 9; 0 ≤ y ≤ 8 (1)

Chi phí cần để thuê xe là: T = 4x + 3y (triệu đồng)

Xe loại A có thể chở tối đa 20 người, xe loại B có thể chở tối đa 10 người, mà số người công ty cần chở là 120 người

⇒ Tổng số người cả hai loại xe có thể chở tối thiểu là 120 người

⇒ 20x + 10y ≥ 120 ⇒ 2x + y ≥ 12  (2)

Xe loại A có thể chở tối đa 0,5 tấn hàng, xe loại B có thể chở tối đa 2 tấn hàng, mà số tấn hàng công ty cần chở là 6,5 tấn

⇒ Tổng số tấn hàng cả hai loại xe có thể chở tối thiểu là 6,5 tấn hàng 

⇒ 0,5x + 2y ≥ 6,5 ⇒ x + 4y ≥ 13 (3)

Từ (1); (2)và (3) ta có hệ bất phương trình: 

$\left\{\begin{array}{l}0\le x\le 9\\ 0\le y\le 8\\ 2x+y\ge 12\\ x+4y\ge 13\end{array}\right.$

Miền nghiệm của hệ là tứ giác ABCD với:

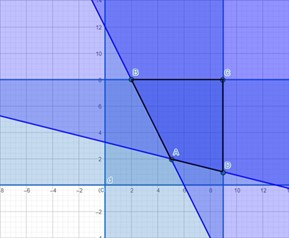A(5; 2) là giao của 2 đường thẳng 2x + y = 12 và x + 4y = 13

B(2; 8) là giao của 2 đường thẳng 2x + y = 12 và y = 8

C(9; 8) là giao của 2 đường thẳng x = 9 và y = 8

D(9; 1) là giao của 2 đường thẳng x = 9 và x + 4y = 13

Tại A(5; 2) thì T = 4.5 + 3.2 = 26 (triệu đồng)

Tại B(2; 8) thì T = 4.2 + 3.8 = 32 (triệu đồng)

Tại C(9; 8) thì T = 4.9 + 3.8 = 60 (triệu đồng)

Tại D(9; 1) thì T = 4.9 + 3.1 = 39 (triệu đồng)

⇒ Chi phí nhỏ nhất là T_min = 26 (triệu đồng)

⇒ Phải thuê 5 chiếc xe loại A và 2 chiếc xe loại B để chi phí bỏ ra là thấp nhất.