Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Vật lí gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Vật lí. Mời các bạn đón xem:

Top 1000 câu hỏi thường gặp môn Vật lí (Phần 6)

Bài 1: Một người đi xe đạp trên $\frac{2}{3}$ đoạn đường đầu với vận tốc trung bình 15 km/h và $\frac{1}{3}$ đoạn đường sau với vận tốc trung bình 20 km/h. Vận tốc trung bình của người đi xe đạp trên cả quãng đường là bao nhiêu?

A. 17,5 km/h.

B. 12 km/h.

C. 15 km/h.

D. 16,36 km/h.

Lời giải

Đáp án đúng: D

Gọi t₁ và t₂ lần lượt là thời gian vật chuyển động với vận tốc 15 km/h và 20 km/h.

Vì độ dài quãng đường đầu gấp 2 lần độ dài quãng đường sau.

Nên ta có: 15.t₁ = 2.20.t₂ => t₂ = \(\frac{3}{8}\).t₁

Vận tốc trung bình trên cả đoạn đường là:

\({v_{tb}} = \frac{{\Delta s}}{{\Delta t}} = \frac{{20.{t_2} + 15.{t_1}}}{{{t_1} + {t_2}}} = \frac{{22,5.{t_1}}}{{\frac{{11}}{8}.{t_1}}} = 16,36km/h\)

Bài 2: Một người đi xe đạp trên $\frac{2}{3}$ đoạn đường đầu với vận tốc trung bình 10 km/h và $\frac{1}{3}$ đoạn đường sau với vận tốc trung bình 20 km/h. Vận tốc trung bình của người đi xe đạp trên cả quãng đường là bao nhiêu?

A. 12 km/h.

B. 15 km/h.

C. 17 km/h.

D. 13,3 km/h.

Lời giải

Đáp án đúng: A

Gọi t₁ và t₂ lần lượt là thời gian vật chuyển động với vận tốc 10 km/h và 20 km/h.

Vì độ dài quãng đường đầu gấp 2 lần độ dài quãng đường sau.

Nên ta có: 10.t₁ = 2.20.t₂ => t₂ = \(\frac{1}{4}\).t₁

Vận tốc trung bình trên cả đoạn đường là:

\({v_{tb}} = \frac{{\Delta s}}{{\Delta t}} = \frac{{20.{t_2} + 10.{t_1}}}{{{t_1} + {t_2}}} = \frac{{15.{t_1}}}{{\frac{5}{4}.{t_1}}} = 12km/h\)

Bài 3: Một ca nô chạy trong hồ nước yên lặng có vận tốc tối đa 18 km/h. Nếu ca nô chạy ngang một con sông có dòng chảy theo hướng Bắc – Nam với vận tốc lên tới 5 m/s thì vận tốc tối đa nó có thể đạt được so với bờ sông là bao nhiêu và theo hướng nào? 

A. \(5\sqrt 2 \)m/s, hướng 45^o Đông – Nam.

B. \(5\sqrt 2 \)m/s, hướng 45^o Đông – Nam.

C. \(5\sqrt 2 \)m/s, hướng 45^o Đông – Bắc.

D. \(5\sqrt 2 \)m/s, hướng 45^o Đông – Bắc.

Lời giải

Đáp án đúng: B

Gọi v₁₃ là vận tốc của ca nô so với bờ sông, v₂₃ là vận tốc của nước so với bờ, v₁₂ là vận tốc của ca nô so với dòng nước.

Đổi v = 18 km/h = 5 m/s

Ca nô sẽ đi theo hướng Đông Nam so với bờ sông với vận tốc tối đa nó có thể đạt được là: \({v_{13}} = \sqrt {{v_{12}}^2 + v_{23}^2}  = \sqrt {{5^2} + {5^2}}  = 5\sqrt 2 \)(m/s)

Bài 4: Người ta dùng một mặt phẳng nghiêng có chiều dài 3 m để kéo một vật có khối lượng 300 kg với lực kéo 1200 N. Có thể kéo vật lên cao bao nhiêu mét? Biết hiệu suất của mặt phẳng nghiêng là 80%.

Lời giải

Công của lực kéo vật lên là:

A = F.s = 1200.3 = 3600 (J)

Công có ích là:

A_i = P.h =10.m.h =10.300.h =3000.h (J)

Độ cao để đưa vật lên là:

H =\(\frac{{{A_i}}}{A}\).100% ⇔ 80% = \(\frac{{3000.h}}{{3600}}\).100%

⇔ h = \(\frac{{3600.80\% }}{{3000.100\% }}\)= 0,96(m)

Bài 5: Thả một hòn đá từ mép một vách núi dựng đứng xuống vực sâu. Sau 4 s từ lúc thả thì nghe thấy tiếng hòn đá chạm đáy vực sâu. Biết g = 9,8 m/s² và tốc độ truyền âm trong không khí là 330 m/s. Tìm chiều cao vách đá bờ vực đó.

A. 76 m.

B. 58 m.

C. 70 m.

D. 82 m.

Lời giải

Đáp án đúng: C

Gọi t₁ là thời gian rơi tự do của hòn đá từ miệng hang xuống đáy: \({t_1} = \sqrt {\frac{{2.h}}{g}} \)(1)

Gọi t₂ là thời gian để âm đi từ đáy đến miệng hang: \({t_2} = \frac{h}{{330}}\)(2)

=> \(\frac{{t_1^2}}{{{t_2}}} = \frac{{\frac{{2h}}{g}}}{{\frac{h}{{330}}}} = \frac{{660}}{g} = \frac{{660}}{{9,8}} \approx 67,3\,\,(3)\)

Mặt khác ta có: t₁ + t₂ = 4(s) => t₂ = 4 – t₁ (4)

Từ (3) và (4) => \(t_1^2 + 67,3.{t_1} - 269,2 = 0\)

=> t₁ = 3,8s hoặc t₁ = -71,1s  < 0 (loại)

Thay t₁ = 3,8 s vào (1) được: \(h = \frac{{g.t_1^2}}{2} = \frac{{9,8.3,{{79}^2}}}{2} \approx 70,4m\)

Bài 6: Thả một hòn đá từ mép một vách núi dựng đứng xuống vực sâu. Sau 3,96 s từ lúc thả thì nghe thấy tiếng hòn đá chạm đáy vực sâu. Biết g = 9,8 m/s² và tốc độ truyền âm trong không khí là 330 m/s. Tìm chiều cao vách đá bờ vực đó.

A. 76 m.

B. 58 m.

C. 69 m.

D. 82 m.

Lời giải

Đáp án đúng: C

Gọi t₁ là thời gian rơi tự do của hòn đá từ miệng hang xuống đáy: \({t_1} = \sqrt {\frac{{2.h}}{g}} \)(1)

Gọi t₂ là thời gian để âm đi từ đáy đến miệng hang: \({t_2} = \frac{h}{{330}}\)(2)

=> \(\frac{{t_1^2}}{{{t_2}}} = \frac{{\frac{{2h}}{g}}}{{\frac{h}{{330}}}} = \frac{{660}}{g} = \frac{{660}}{{9,8}} \approx 67,3(3)\)

Mặt khác ta có t₁ + t₂ = 3,96(s) (4)

Từ (3) và (4) =>\(t_1^2 + 67,3.{t_1} - 266,508 = 0\)=> t₁ = 3,75s hoặc t₁ = -71,05s < 0 (loại)

Thay t₁ = 3,75 s vào (1) được: \(h = \frac{{g.t_1^2}}{2} = \frac{{9,8.{{(3,75)}^2}}}{2} \approx 69m\)

Bài 7: Một người đi xe đạp đi nửa quãng đường đầu với vận tốc v₁ = 12 km/h, nửa quãng đường sau đi với vận tốc v₂ nào đó. Biết rằng vận tốc trung bình trên cả quãng đường là 8 km/h. Hãy tính vận tốc v₂.

Lời giải

Gọi s là chiều dài nửa quãng đường mà người đi xe đạp phải đi.

Như vậy, thời gian đi hết nửa quãng đường đầu s₁ = s với vận tốc v₁ là:

\({t_1} = \frac{{{s_1}}}{{{v_1}}} = \frac{s}{{{v_1}}}\)(h)

Thời gian đi hết nửa quãng đường còn lại s₂ = s với vận tốc v₂ là:

\({t_2} = \frac{{{s_2}}}{{{v_2}}} = \frac{s}{{{v_2}}}\)(h)

Vậy tổng thời gian đi hết cả quãng đường là: \({t_1} + {t_2} = \frac{s}{{{v_1}}} + \frac{s}{{{v_2}}}\)(h)

Vận tốc trung bình của người đi xe đạp trên cả quãng đường là:

\({v_{tb}} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{{2s}}{{\frac{s}{{{v_1}}} + \frac{s}{{{v_2}}}}} = \frac{{2s}}{{\left( {\frac{1}{{{v_1}}} + \frac{1}{{{v_2}}}} \right).s}} = \frac{2}{{\frac{1}{{{v_1}}} + \frac{1}{{{v_2}}}}}\)

\( \Rightarrow \frac{1}{{{v_1}}} + \frac{1}{{{v_2}}} = \frac{2}{{{v_{tb}}}}\)

\( \Rightarrow \frac{1}{{{v_2}}} = \frac{2}{{{v_{tb}}}} - \frac{1}{{{v_1}}} = \frac{2}{8} - \frac{1}{{12}}\)

\( \Rightarrow \frac{1}{{{v_2}}} = \frac{1}{6} \Rightarrow {v_2} = 6\,km/h\)

Bài 8: Một người đi xe đạp đi nửa quãng đường đầu với vận tốc 12 km/h và nửa quãng đường còn lại với vận tốc 20 km/h. Hãy xác định vận tốc trung bình của người đi xe đạp trên cả quảng đường.

Lời giải

Gọi thời gian xe đi đoạn nửa đoạn đầu và nửa đoạn sau là: t₁ và t₂
Thời gian xe đi nửa quãng đường đầu: \[{t_1} = \frac{{{s_1}}}{{{v_1}}} = \frac{{\frac{s}{2}}}{{12}} = \frac{s}{{24}}\] (h)

Thời gian xe đi nửa quãng đường sau: \[{t_2} = \frac{{{s_2}}}{{{v_2}}} = \frac{{\frac{s}{2}}}{{20}} = \frac{s}{{40}}\] (h)
Vận tốc trung bình của xe là: \[{v_{tb}} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{s}{{\frac{s}{{24}} + \frac{s}{{40}}}} = \frac{1}{{\frac{1}{{24}} + \frac{1}{{40}}}} = 15km/h\]

Bài 9: Từ đỉnh tháp cao 80 m so với mặt đất, ném một vật nhỏ theo phương ngang với vận tốc ban đầu v₀ = 30 m/s. Bỏ qua lực cản của không khí. Lấy g = 10 m/s².

a. Tính thời gian chuyển động của vật đến khi chạm đất.

b. Xác định tầm bay xa của vật.

Lời giải

a. Thời gian vật chạm đất là: \[t = \sqrt {\frac{{2.h}}{g}}  = \sqrt {\frac{{2.80}}{{10}}}  = 4s\]

b. Tầm bay xa là: L = v₀.t = 30.4 = 120 (m)

Bài 10: Lúc 7 h một người đi xe đạp với vận tốc 10 km/h xuất phát từ A hướng về B. Đến 8 h một người đi xe máy với vận tốc 30 km/h cũng xuất phát ở A đuổi theo xe đạp. Đến 9 h một ô tô cũng xuất phát ở A đuổi theo hai xe kia với vận tốc 40 km/h. Tìm thời điểm để 3 xe cách đều nhau lần đầu tiên, khi đó xe máy cách A bao xa?

Lời giải

Đến 9 h xe đạp đi được đoạn đường là:

S₁ = v₁.t₁ = 10.(9 - 7) = 20 (km)

Đến 9 h xe máy đi được đoạn đường là:

S₂ = v₂.t₂ = 30.(9 - 8) = 30 (km)

Khi xe 3 xuất phát thì xe máy đang dẫn đầu.

Thời điểm 3 xe cách đều nhau thì xe máy đi đầu, xe đạp và ô tô 

Gọi thời gian xe đạp đi đến khi cách đều 2 xe là: t (giờ) ( t > 2)

Các xe cách đều 1 quãng đường là: 

S₂ − S₁ = S₁ − S₃

⇔ 30.(t −1) −10.t = 10.t − 40.(t − 2)

⇒ t = 2,2 h = 2 giờ 12 phút

Thời điểm đầu tiên 3 xe cách đều nhau là:

7 giờ + 2 giờ 12 phút = 9 giờ 12 phút

Vị trí đó cách A số km là:

2,2 . 10 = 22 (km)

Đáp số: 9 giờ 12 phút và 22 km

Bài 11: Sóng dừng trên sợi dây đàn hồi với bước sóng 1,2 cm. Hai điểm A, B trên dây, biết AB = 7 cm và tại A là một bụng sóng. Tính số bụng sóng và nút sóng có trên đoạn dây AB.

A. 11 bụng, 12 nút.

B. 12 bụng, 13 nút.

C. 12 bụng, 12 nút.

D. 12 bụng, 11 nút.

Lời giải

Đáp án đúng: C

AB = 7 cm = 11.0,6 + 0,4 (cm) = 11.\(\frac{\lambda }{2}\)+ 0,4 (cm)

Vì tại A là một bụng sóng nên trong khoảng cách 11.\(\frac{\lambda }{2}\) ta có được 11 nút sóng.

Khoảng cách từ bụng đến nút gần nhất là \(\frac{\lambda }{4}\). Mà 0,4 >\(\frac{\lambda }{4}\)

=> Trong khoảng 0,4cm có thêm 1 nút sóng nữa. Mà số bụng = số nút.

Như vậy trên đoạn AB có 12 nút sóng.

Bài 12: Đổi đơn vị

1mC =.. ....C

1uC=......C

1nC......C

1pC......C

Lời giải

1mC = 10^-3C

1uC = 10^-6C

1nC = 10^-9C

1pC = 10^-12C

Bài 13: Một đoàn tàu bắt đầu chạy vào một đoạn đường tròn, bán kính 1 km, dài 600 m, với vận tốc 54 km/h. Đoàn tàu chạy hết quãng đường đó trong 30 s. Tìm vận tốc dài, gia tốc pháp tuyến, gia tốc tiếp tuyến, gia tốc toàn phần và gia tốc góc của đoàn tàu ở cuối quãng đường đó. Coi chuyển động của đoàn tàu là nhanh dần đều.

Lời giải

Đổi 54 km/h = 15 m/s

Gia tốc tiếp tuyến ở cuối cung đường là:

v = v_o + a_tt.t = 15 + 30. a_tt

Lại có v² - 15² = 2. a_tt .600

=> v = 85 (km/h); a_tt = \(\frac{7}{3}\) (m/s²)

Vậy gia tốc tiếp tuyến ở cuối cung đường là: a_tt = \(\frac{7}{3}\)m/s²

Gia tốc hướng tâm ở cuối cung đường là:

\({a_n} = \frac{{{{85}^2}}}{{1000}} = 7,225m/{s^2}\)

Gia tốc toàn phần ở cuối cung đường là:

\(a = \sqrt {{a_{tt}}^2 + a_n^{\rm{2}}}  = \sqrt {{{\left( {\frac{7}{3}} \right)}^2} + 7,{{225}^2}} \)= 7,59 m/s²

Bài 14: Một giọt thủy ngân hình cầu bán kính 1 mm tích điện q = 3,2.10^-13C đặt trong không khí. Tính cường độ điện trường và điện thế của giọt thủy ngân trên bề mặt giọt thủy ngân.

A. 2880 V/m; 2,88 V.

B. 3200 V/m; 2,88 V.

C. 3200 V/m; 3,2 V.

D. 2880 V/m; 3,45 V.

Lời giải

Đáp án đúng: A

Cường độ điện trường trên bề mặt giọt thủy ngân là: \(E = k\frac{{\left| q \right|}}{{{r^2}}} = \frac{{\left| {3,{{2.10}^{ - 13}}} \right|}}{{{{\left( {{{10}^{ - 3}}} \right)}^2}}} = 2880V/m\)

Điện thế của giọt thủy ngân trên bề mặt giọt thủy ngân là

V = E.d = 2800 . 0,001 = 2,88 V

Bài 15: Một ô tô đi được quãng đường dài 60 km với vận tốc 48 km/h. Hỏi ô tô đó đã đi hết bao nhiêu thời gian?

Lời giải

Ô tô đó đã đi hết số thời gian là: \(t = \frac{s}{v} = \frac{{60}}{{48}} = 1,25(h)\) = 1 giờ 15 phút

Bài 16: Đặt vật AB vuông góc với trục chính của thấu kính hội tụ có tiêu cự f = 20 cm, sao cho điểm A nằm trên trục chính và cách thấu kính một khoảng d = 30cm.

a) Hãy xác định vị trí và tính chất (thật hay ảo) của ảnh.

b) Biết AB = 4 cm. Tìm chiều cao của ảnh

Lời giải

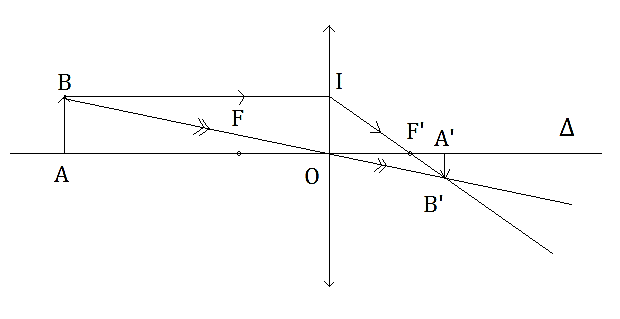
OA = d = 30cm; OF = f = 20cm

a. Theo đề bài: f < d < 2f

⇒ Ảnh thật, ngược chiều và lớn hơn vật

b. Ta có: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\) ⇔\(\frac{1}{{20}} = \frac{1}{{30}} + \frac{1}{{d'}}\) ⇔d’ = OA′ = 60 (cm)

ΔABO∼ΔA′B′O(g.g)

⇒\(\frac{{AB}}{{A'B'}} = \frac{{OA}}{{OA'}}\)⇔A′B′ =\(\frac{{AB.OA'}}{{OA}}\) = \(\frac{{4.60}}{{30}}\)= 8(cm)

Bài 17: Một thấu kính hội tụ có tiêu cự 20 cm. Vật sáng AB vuông góc với trục chính thấu kính tại A, cách thấu kính 30 cm. Ảnh tạo bởi thấu kính có đặc điểm gì?
A. Cách thấu kính 60 cm, cao gấp 2 lần vật, cùng chiều với vật

B. Cách thấu kính 60 cm, cao gấp 2 lần vật, ngược chiều với vật.

C. Cách thấu kính 10 cm, cao bằng nửa vật, cùng chiều với vật.

D. Cách thấu kính 10 cm, cao bằng nửa vật, ngược chiều với vật.

Lời giải

Đáp án đúng: B

Theo đề bài: f < d < 2f  => Ảnh tạo bởi thấu kính hội tụ là ảnh thật, ngược chiều và lớn hơn vật.

Ta có \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\) ⇔\(\frac{1}{{20}} = \frac{1}{{30}} + \frac{1}{{d'}}\) ⇔d’ = OA′ = 60 (cm)

Lại có \(\frac{h}{{h'}} = \frac{d}{{d'}} = \frac{{30}}{{60}} = \frac{1}{2}\)=> h = \(\frac{1}{2}\)h’ hay AB = \(\frac{1}{2}\)A’B’

Bài 18: Thả một vật làm bằng kim loại vào bình đo thể tích có vạch chia độ thì nước trong bình từ vạch 180 cm³ tăng đến vạch 265 cm³. Nếu treo vật vào một lực kế trong điều kiện vật vẫn nhúng hoàn toàn trong nước thấy lực kế chỉ 7,8 N.

a. Tính lực đẩy Acsimét tác dụng lên vật.
b. Xác định khối lượng riêng của chất làm vật.

Lời giải

Vì vật làm bằng kim loại nên vật chìm hoàn toàn trong nước.

Ta có, thể tích nước dâng lên chính bằng thể tích của vật.

⇒ V_d = V = 265 − 180 = 85 cm³ = 8,5.10^-5 m³

Lực đẩy Acsimet tác dụng lên vật: F_A = d.V = 10000.8,5.10⁻⁵ = 0,85 N

Nếu treo vật vào một lực kế trong điều kiện vật vẫn nhúng hoàn toàn trong nước thì khi đó vật chịu tác dụng của trọng lực P và lực đẩy Acsimet F_A. Hai lực này có cùng phương nhưng ngược chiều nhau.

=> P – F_A = 7,8N

ó P = F_A + 7,8 = 0,85 + 7,8 = 8,65N

Mặc khác trọng lượng của vật P = 10.D_v.V

=> D_v = P : 10V = 8,65 : (10.8,5.10⁻⁵ )

⇒ D_v = 10176 (kg/m³)

Bài 19: Một vật có khối lượng 4,5 kg được treo vào một sợi dây. Cần phải giữ dây một lực bằng bao nhiêu để vật được cân bằng? Vẽ hình, phân tích lực, biểu diễn lực, nêu đặc điểm của lực trên hình vẽ. Lấy g \( \approx \)10 m/s².

Lời giải

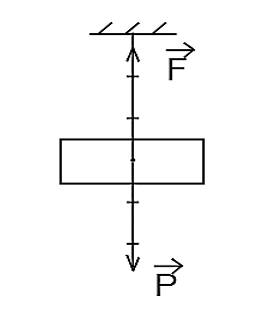
- Có 2 lực tác dụng lên vật:

+ Trọng lực có phương thẳng đứng, chiều từ trên xuống.

+ Lực kéo của sợi dây có phương thẳng đứng, chiều từ dưới lên.

- Để vật cân bằng thì 2 lực tác dụng lên vật phải là 2 lực cân bằng.

Vậy lực kéo của sợi dây là: F_k = P = m.g = 4,5.10 = 45N.

Bài 20: Một vật có khối lượng 4,5 kg được buộc vào một sợi dây. Cần phải giữ dây một lực bằng bao nhiêu để vật được cân bằng? Chọn kết quả đúng. Lấy g \( \approx \)10 m/s² .

A. F > 45 N.

B. F = 45 N.

C. F < 45 N.

D. F  = 4,5 N.

Lời giải

Đáp án đúng: B

- Có 2 lực tác dụng lên vật:

+ Trọng lực có phương thẳng đứng, chiều từ trên xuống

+ Lực kéo của sợi dây có phương thẳng đứng, chiều từ dưới lên

- Để vật cân bằng thì 2 lực tác dụng lên vật phải là 2 lực cân bằng.

Vậy lực kéo của sợi dây là: F_k = P = m.g = 4,5.10 = 45N

Bài 21: Một viên bi lăn xuống 1 cái dốc dài 1,2 m hết 0,5 giây. Khi hết dốc, bi lăn tiếp 1 quãng đường nằm ngang dài 3 m trong 1,4 giây. Tính vận tốc trung bình của viên bi trên quãng đường dốc, trên quảng đường nằm ngang và trên cả 2 quãng đường.

Lời giải

Vận tốc trung bình trên dốc: 

v₁ = \(\frac{{{s_1}}}{{{t_1}}}\) = \(\frac{{1,2}}{{0,5}}\)= 2,4 m/s 

Vận tốc trung bình trên đường ngang:

v₂ = \(\frac{{{s_2}}}{{{t_2}}}\) = \(\frac{3}{{1,4}}\)= 2,1 m/s 

Vận tốc trung bình cả quãng đường: 

V = \(\frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}}\) = \(\frac{{1,2 + 3}}{{0,5 + 1,4}}\) = 2,2 m/s

Bài 22: Một viên bi được thả lăn xuống dốc dài 1,2 m với vận tốc trung bình là 2,4 m/s. Khi hết dốc, nó lăn tiếp một quãng đường nằm ngang dài 3 m trong 1,4 s.

a. Tính vận tốc trung bình của viên bi trên quãng đường nằm ngang và trên cả 2 quãng đường.

b. Nêu nhận xét về các kết quả tìm được.

Lời giải

a. Thời gian mà bi lăn trên quãng đường dốc là:

 \({t_1} = \frac{{{s_1}}}{{{v_1}}} = \frac{{1,2}}{{2,4}} = 0,5s\)

Vận tốc mà bi lăn trên quãng đường nằm ngang là:

\({v_2} = \frac{{{s_2}}}{{{t_2}}} = \frac{3}{{1,4}} \approx 2,143m/s\)

Vận tốc trung bình mà viên bi lăn trên cả 2 quãng đường là:

\({v_{tb}} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{{1,2 + 3}}{{1,4 + 0,5}} = \frac{{4,2}}{{1,9}} \approx 2,21\,m/s\)

b. Nhận xét: Vận tốc trên quãng đường dốc khác vận tốc trên quãng đường nằm ngang khác vận tốc trung bình trên cả hai quãng đường.

Bài 23: Cho mạch điện như hình vẽ: R₁ = R₂ = R₃ = 6Ω , R₄ = 2Ω . Tính điện trở tương đương của mạch khi ta nối M và B bằng một ampe kế có điện trở rất nhỏ?

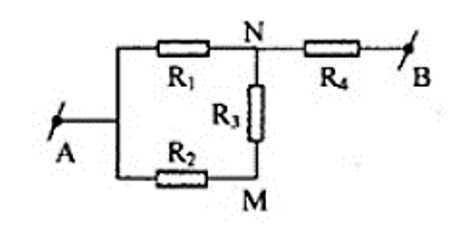
A. R = 20 Ω.

B. R = \(\frac{9}{3}\Omega \) .

C. R = \(\frac{{10}}{3}\Omega \).

D. R = 14Ω.

Lời giải

Đáp án đúng: C

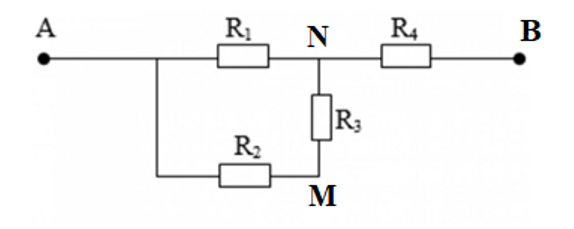
Vì ampe kế có điện trở rất nhỏ nên M và B cùng điện thế.

=> Chập M và B mạch điện được vẽ như hình.

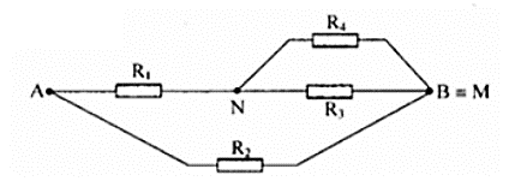
Ta có R₂ // (R₁ nt (R₃//R₄))

\(\begin{array}{l}\frac{1}{{{R_{34}}}} = \frac{1}{{{R_3}}} + \frac{1}{{{R_4}}} =  > {R_{34}} = \frac{{{R_3}.{R_4}}}{{{R_3} + {R_4}}} = \frac{{6.2}}{{6 + 2}} = 1,5\Omega \\{R_{134}} = {R_1} + {R_{34}} = 6 + 1,5 = 7,5\Omega \end{array}\)

Điện trở tương đương của toàn mạch:

\[\frac{1}{R} = \frac{1}{{{R_2}}} + \frac{1}{{{R_{134}}}} =  > R = \frac{{{R_2}.{R_{134}}}}{{{R_2} + {R_{134}}}} = \frac{{6.7,5}}{{6 + 7,5}} = \frac{{10}}{3}\Omega \]

Bài 24: Cho mạch điện như hình vẽ: R₁ = R₂ = R₃ = 6 W ; R₄ = 2 W; U_AB = 18 V. Nối M và B bằng một vôn kế. Tìm số chỉ của vôn kế B. Nối M và B bằng 1 ampe kế điện trở không đáng kể. Tìm số chỉ của ampe kế, chiều dòng qua Ampe kế.

Lời giải

a. Nối M, B bằng một vôn kế

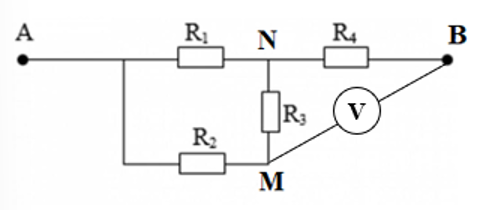
Vi điện trở của vôn kế rất lớn nên ta có thể bỏ vôn kế ra khỏi mạch.

Mạch: \(\left[ {R{}_1//\left( {{R_2}\,nt\,{R_3}} \right)} \right]\,\,nt\,{R_4}\)

\({R_{23}} = {R_2} + {R_3} = 6 + 6 = 12\Omega \)

\({R_{123}} = \frac{{{R_1}.R{}_{23}}}{{{R_1} + R{}_{23}}} = \frac{{12.6}}{{12 + 6}} = 4\Omega \)

\({R_{1234}} = {R_{123}} + {R_4} = 4 + 2 = 6\Omega \)

\({I_{AB}} = {I_4} = {I_{123}} = \frac{{{U_{AB}}}}{{{R_{1234}}}} = \frac{{18}}{6} = 3A\)

U₄ = I₄.R₄ = 3.2 = 6 V

U₂₃ = U₁₂₃ = I₁₂₃ . R₁₂₃ = 3.4 = 12V

I₃ = I₂₃ = U₂₃ : R₂₃ = 12 :12 = 1 A

U₃ = I₃ . R₃ = 1.6 = 6 V

\( \Rightarrow {U_V} = {U_3} + {U_4} = 6 + 6 = 12V\) là số chỉ của vôn kế.

b. Nối M, B bằng ampe kế

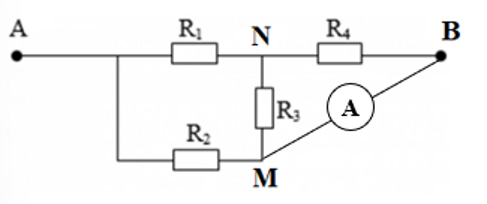
Vì điện trở của ampe kế rất nhỏ nên chập hai điểm M, B vì có cùng điện thế.

Mạch trở thành:

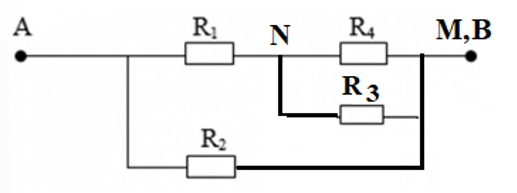
Mạch: \[\left[ {{R_1}\,nt\,\,\left( {{R_4}//{R_3}} \right)} \right]//{R_2}\]

\(R{}_{34} = \frac{{{R_3}.{R_4}}}{{{R_3} + {R_4}}} = \frac{{6.2}}{{6 + 2}} = 1,5\Omega \)

\({R_{134}} = {R_1} + {R_{34}} = 6 + 1,5 = 7,5\Omega \)

\({I_2} = \frac{{{U_{AB}}}}{{{R_2}}} = \frac{{18}}{6} = 3A\)

\({I_{34}} = {I_{134}} = \frac{{{U_{AB}}}}{{{R_{134}}}} = \frac{{18}}{{7,5}} = 2,4A\)

\( \Rightarrow {U_3} = {I_{34}}.{R_{34}} = 2,4.1,5 = 3,6V\)

\( \Rightarrow {I_3} = \frac{{{U_3}}}{{{R_3}}} = \frac{{3,6}}{6} = 0,6A\)

\( \Rightarrow {I_A} = {I_3} + {I_4} = 3 + 0,6 = 3,6A\)

Vậy số chỉ ampe kế là 3,6 A. Chiều dòng điện qua ampe kế là từ M đến B.

Bài 25: Trên một bóng đèn có ghi 6V - 5W. Mắc đèn này vào hiệu điện thế đúng bằng hiệu điện thế định mức của nó trong 2 giờ.

a, Tính điện trở của đèn khi đó.

b, Tính tiền điện phải trả khi sử dụng đèn trong 30 ngày .Biết 1kWh = 700đ

Lời giải

a. Điện trở của đèn khi đó là

\(R = \frac{{{U^2}}}{P} = \frac{{{6^2}}}{5} = 7,2\left( \Omega  \right)\)

b. Điện năng tiêu thụ là

A = P . t = 5.30.2.3600 = 1080000 (W.s) = 0,3 kWh

Số tiền phải trả khi sử dụng đèn là T = A. 700 = 0,3 .700 = 210 (đ)

Bài 26: Một quả cầu nặng m = 100 g được treo ở đầu một sợi dây nhẹ, không co dãn, dài l = 1 m (đầu kia của dây cố định). Truyền cho quả cầu ở vị trí cân bằng một vận tốc đầu v₀ theo phương ngang. Khi dây treo nghiêng góc α =30⁰ so với phương thẳng đứng thì gia tốc của quả cầu có phương ngang. Cho g = 10 m/s², bỏ qua mọi ma sát.

a) Tìm vận tốc v₀.

b) Tính lực căng dây và vận tốc của vật tại vị trí có góc lệch a = 40⁰.

Lời giải

a. Khi dây treo nghiêng góc \(\alpha  = {30^0}\) so với phương thẳng đứng, vật M chịu tác dụng của các lực như hình vẽ. Do gia tốc có phương ngang nên

T . cos 30⁰ = m.g (1)

Mặt khác, xét theo phương hướng tâm MO ta có:

\(T - mg.cos{30^0} = \frac{{m{v^2}}}{\ell }\) (2) (Với v là vận tốc của vật tại M)

Từ (1) và (2) suy ra: \({v^2} = \frac{{g\ell }}{{2\sqrt 3 }}\,\,(3)\)

Áp dụng ĐLBT cơ năng cho hệ khi vật ở vị trí M và khi vật ở vị trí cân bằng ta được:

\(v_0^2 = {v^2} + 2g\ell \left( {1 - cos{{30}^0}} \right) = \frac{{12 - 5\sqrt 3 }}{6}g\ell \)

\( \Rightarrow {v_0} = 2,36\,m/s\)

b. Áp dụng ĐLBT cơ năng cho hệ khi vật ở vị trí \(\alpha  = {40^0}\)và khi vật ở vị trí cân bằng ta được:

\(v_0^2 = {v^2} + 2g\ell \left( {1 - cos{{40}^0}} \right)\)\( \Rightarrow v = \sqrt {v_0^2 - 2g\ell \left( {1 - cos{{40}^0}} \right)}  \approx 0,94\,m/s\)

Xét theo phương sợi dây ta có:

T = m.g.cos40⁰ + \(\frac{{m{v^2}}}{\ell }\)= 0,1.10.cos40⁰ + \(\frac{{0,1.0,{{94}^2}}}{1} = 0,86\,N\)

Bài 27: Tính chiều cao của một cây cổ thụ có bóng trên mặt đất dài 8 m và có tia sáng từ đỉnh tạo với mặt đất một góc bằng 60⁰.

Lời giải

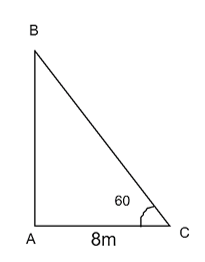
Theo hình vẽ ta có: \(\tan \widehat {BCA} = \frac{{AB}}{{AC}} = \frac{{AB}}{8} \Rightarrow \tan {60^0} = \frac{{AB}}{8} \Rightarrow AB = 8\sqrt 3 (m)\)

Bài 28: Bên cạnh nhà bạn An có một cái cây cổ thụ. Bố An muốn đo chiều cao của cây nhưng không thể trèo lên cây được, An đã giúp bố đo chiều cao của cây cổ thụ bằng cách đo bóng cây trên mặt đất dài 8 m và có tia sáng từ đỉnh tạo với mặt đất một góc bằng 60⁰. Em hãy giúp An tính chiều cao cây cổ thụ cho bố (làm tròn kết quả đến hàng đơn vị).

Lời giải

Giả sử AB là cây cổ thụ, AC là độ dài bóng của cây in trên mặt đất.

Ta có hình vẽ như sau:

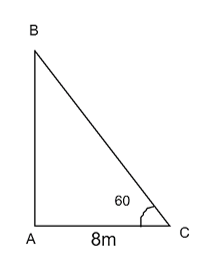
\(\tan \widehat {BCA} = \frac{{AB}}{{AC}} = \frac{{AB}}{8} \Rightarrow \tan {60^0} = \frac{{AB}}{8} \Rightarrow AB = 8\sqrt 3 (m) \approx 13,86m\)

Vậy cây cổ thụ có chiều cao khoảng 13,86 m.

Bài 29: Thế nào là áp suất khí quyển? Áp suất này tác dụng lên các vật trong khí quyển theo phương nào? Nêu ví dụ cho thấy tác dụng của áp suất khí quyển?

Lời giải               

- Do không khí có trọng lượng nên Trái Đất và mọi vật trên Trái Đất đều chịu áp suất của lớp không khí bao quanh Trái Đất. Áp suất này được gọi là áp suất khí quyển.

- Áp suất khí quyển tác dụng lên các vật trong khí quyển theo mọi phương.

Ví dụ:

- Khi bác sĩ truyền nước cho bệnh nhân, lúc chai nước gần hết thì ta thấy chai nước bị bóp méo lại.

- Em bé hút một hộp sữa giấy, khi sữa trong hộp hết thì hộp bị bẹp theo nhiều phía.

Bài 30: Nêu ví dụ chứng tỏ sự tồn tại của áp suất khí quyển.

Lời giải

- Trên nắp các bình nước lọc thường có một lỗ nhỏ thông với khí quyển để lấy nước dễ dàng hơn.

- Các bình pha trà thường có một lỗ nhỏ trên nắp để thông với khí quyển, như thế sẽ rót nước dễ hơn.

– Hút bớt không khí trong vỏ hộp sữa bằng giấy, ta thấy vỏ hộp bị bẹp theo nhiều phía

– Lấy 1 cây kim chọc 1 đầu quả trứng ta thấy trứng ko chảy ra chọc thêm 1 đầu đối diện thì trứng chảy ra.

Bài 31: Một đoàn xe cơ giới có đội hình dài 1500 m di chuyển với vận tốc 40 km/h. Người chỉ huy ở đầu xe trao cho một chiến sĩ đi mô tô một mệnh lệnh chuyển xuống xe cuối. Chiến sĩ ấy đi và về với cùng một vận tốc và hoàn thành nhiệm vụ trở về báo cáo mất một thời gian 5 phút 24 s. Tính tốc độ chiến sĩ đi mô tô.

A. 60 km/h.

B. 54 km/h.

C. 18 km/h.

D. 20 km/h.

Lời giải

Đáp án đúng: A

Đổi 5 min 24 s = 324 s

Gọi v₁₀ là tốc độ chiến sĩ đi mô tô so với mặt đường, v₂₀ là tốc độ đoàn xe so với mặt đường, v₁₂ là tốc độ chiến sĩ đi mô tô so với đoàn xe.

Quãng đường người chiến sĩ đi xe mô tô ở cả lượt đi và lượt về là như nhau và cùng bằng l = 1500 m.

Ta có: \({\vec v_{12}} = {\vec v_{10}} + {\vec v_{02}} = {\vec v_{10}} + \left( { - {{\vec v}_{20}}} \right)\)

+ Chọn chiều dương là chiều chuyển động của người chiến sĩ đi xe mô tô  

\(\left\{ {\begin{array}{*{20}{c}}{{v_{12\left( {di} \right)}} = {v_{10}} + {v_{20}}}\\{{v_{12\left( {ve} \right)}} = {v_{10}} - {v_{20}}}\end{array}} \right.\)

+ Theo đề bài suy ra: \(t = \frac{\ell }{{{v_{10}} + {v_{20}}}} + \frac{\ell }{{{v_{10}} - {v_{20}}}} = 324(s)\)

\( \Rightarrow \frac{{1500}}{{{v_{10}} + \frac{{100}}{9}}} + \frac{{1500}}{{{v_{10}} - \frac{{100}}{9}}} = 324\)

\( \Rightarrow 0,216v_{10}^2 - 2{v_{10}} - \frac{{80}}{3} = 0\)

\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{{v_{10}} = \frac{{50}}{3}\,(m/s)}\\{{v_{10}} =  - \frac{{200}}{{27}}\,(m/s)}\end{array}} \right.\)

Ta nhận giá trị v₁₀ dương, v₁₀ = 16,67 m/s = 60 km/h

Vậy tốc độ chiến sĩ đi mô tô là 60 km/h.

Bài 32: Một đoàn xe cơ giới có đội hình dài 1500 m hành quân với vận tốc 40 km/h. Người chỉ huy ở xe đầu trao cho một chiến sĩ đi mô tô một mệnh lệnh chuyển xuống xe cuối. Chiến sĩ ấy đi và về với cùng một vận tốc và hoàn thành nhiệm vụ trở về báo cáo mất một thời gian 5 phút 24 giây. Vận tốc của chiến sĩ đi mô tô là

A. 16,67 m/s.

B. 44,8 km/h.

C. 44,9 m/s.

D. 16,67 km/h.

Lời giải

Đáp án đúng: A

Đổi 5 min 24 s = 324 s

Gọi v₁₀ là tốc độ chiến sĩ đi mô tô so với mặt đường, v₂₀ là tốc độ đoàn xe so với mặt đường, v₁₂ là tốc độ chiến sĩ đi mô tô so với đoàn xe.

Quãng đường người chiến sĩ đi xe mô tô ở cả lượt đi và lượt về là như nhau và cùng bằng l = 1500 m.

Ta có: \({\vec v_{12}} = {\vec v_{10}} + {\vec v_{02}} = {\vec v_{10}} + \left( { - {{\vec v}_{20}}} \right)\)

+ Chọn chiều dương là chiều chuyển động của người chiến sĩ đi xe mô tô  

\(\left\{ {\begin{array}{*{20}{c}}{{v_{12\left( {di} \right)}} = {v_{10}} + {v_{20}}}\\{{v_{12\left( {ve} \right)}} = {v_{10}} - {v_{20}}}\end{array}} \right.\)

+ Theo đề bài suy ra: \(t = \frac{\ell }{{{v_{10}} + {v_{20}}}} + \frac{\ell }{{{v_{10}} - {v_{20}}}} = 324(s)\)

\( \Rightarrow \frac{{1500}}{{{v_{10}} + \frac{{100}}{9}}} + \frac{{1500}}{{{v_{10}} - \frac{{100}}{9}}} = 324\)

\( \Rightarrow 0,216v_{10}^2 - 2{v_{10}} - \frac{{80}}{3} = 0\)

\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{{v_{10}} = \frac{{50}}{3}\,(m/s)}\\{{v_{10}} =  - \frac{{200}}{{27}}\,(m/s)}\end{array}} \right.\)

Ta nhận giá trị v₁₀ dương, v₁₀ = 16,67 m/s

Vậy tốc độ chiến sĩ đi mô tô là 16,67 m/s.

Bài 33: Một bàn là được sử dụng đúng với hiệu điện thế định mức 220 V trong 30 phút thì tiêu thụ một điện năng là 1440 kJ.

a. Tính công suất của bàn là?

b. Tính điện trở của bàn là và cường độ dòng điện chạy qua nó khi đó?

Lời giải

A =1440 kJ =1400000 J

a) Công suất của bàn là là:

P = At = 1440.10330.60 = 800 (W)

b. Cường độ dòng điện chạy qua bàn là:

I = P : U = 800 : 220 = 3,64 (A)

Điện trở của bàn là là:

R = U : I = 220 : 3,64 = 60,44(Ω)

Bài 34: Cho mạch điện gồm 3 điện trở mắc nối tiếp nhau. Biết R₁ = R₂ = 4R₃. Hiệu điện thế giữa hai đầu đoạn mạch là U = 90 V. Cường độ dòng điện qua R3 là 2A. Tính giá trị mỗi điện trở.

Lời giải

Mạch: R₁ nt R₂ nt R₃

Cường độ dòng điện trong mạch chính:

I = I₃ = 2 A

Điện trở tương đương của đoạn mạch:

R_tđ = U : I = 90 : 2 = 45 (Ω)

Ta có:

R₁ + R₂ + R₃ = R_tđ

\( \Rightarrow \)4 R₃ + 4 R₃ + R₃ = 45

\( \Rightarrow \) 9 R₃ = 45

\( \Rightarrow \)R₃ = 5 (Ω)

\( \Rightarrow \) R₁ = R₂ = 4R₃ = 4.5 = 20 (Ω)

Bài 35: Một hòn sỏi được ném thẳng đứng xuống dưới với vận tốc ban đầu bằng 9.8 m/s từ độ cao 39,2 m. Lấy g = 9,8 m/s². Bỏ qua lực cản không khí. Vận tốc của hòn sỏi ngay trước khi chạm đất là

A. 9,8 m/s.

B. 19,6 m/s.

C. 29,4 m/s.

D. 38,2 m/s.

Lời giải

Đáp án đúng: C

\({v^2} - v_0^2 = 2gh \Rightarrow v = \sqrt {2gh + v_0^2}  = \sqrt {2.9,8.39,2 + 9,{8^2}}  = 29,4m/s\).

Bài 36: Một hòn sỏi được ném thẳng đứng xuống dưới với vận tốc ban đầu bằng 9.8m/s từ độ cao 39,2 m. Lấy g = 9,8 m/s². Bỏ qua lực cản không khí. Hòn bi rơi tới đất sau khoảng thời gian là

A. 1 s.             B. 2 s.             C. 3 s.             D. 4 s.

Lời giải

Đáp án đúng: B

Từ \(s = {v_0}.t + \frac{1}{2}g{t^2} \Rightarrow 4,9{t^2} + 9,8t - 39,2 = 0 \Rightarrow t = 2(s)\).

Bài 37: Hai người đi bộ khởi hành ở hai địa điểm khác nhau 4,18 km đi ngược chiều nhau để gặp nhau. Người thứ nhất mỗi giờ đi đc 5,7 km, người thứ hai mỗi giờ đi được 6,3 km nhưng xuất phát sau người thứ nhất 4 phút. Hỏi người thứ hai đi trong bao lâu thì gặp người thứ nhất.

Lời giải

Gọi t là thời gian người thứ 2 gặp người thứ nhất (t (h) > 0).

Ta có, thời gian người thứ nhất đi là \(t + \frac{1}{{15}}(h)\), thời gian người thứ hai đi là t (h)

Quãng đường người thứ nhất đi được là s₁ = 5,7 . \(\left( {t + \frac{1}{{15}}} \right)\) (km)

Quãng đường người thứ hai đi được là  s₂ = 6,3.t (km)

Theo đề bài: s₁ + s₂ = 4,18 \( \Leftrightarrow 5,7\left( {t + \frac{1}{{15}}} \right) + 6,3t = 4,18\)

\( \Rightarrow \)12t + 0,38 = 4,18 \( \Rightarrow t = \frac{{19}}{{60}}\,(h) = 19\min \)

Bài 38: Lúc 8 h một người đi xe đạp với vận tốc đều 12 km/h gặp một người đi bộ đi ngược chiều với vận tốc đều 4 km/h trên cùng đoạn đường thẳng. Tới 8 h 30 phút người đi xe đạp dừng lại, nghỉ 30 phút rồi quay trở lại đuổi theo người đi bộ với vận tốc có độ lớn như trước. Xác định lúc và nơi người đi xe đạp đuổi kịp người đi bộ.

Lời giải

Chọn gốc tọa độ O tại vị trí người đi xe đạp dừng lại nghỉ, trục tọa độ là quỹ đạo chuyển động của hai người, chiều dương là chiều chuyển động của người đi bộ; gốc thời gian lúc 9 h.

- Phương trình chuyển động của hai người là

+ Xe đạp: x₀₁ = 0, v₁ = 12 km/h, t₀₁ = 0

X₁ = x₀₁ + v₁ (t – t₀₁) = 12t (1)

+ Người đi bộ: x₀₂ = 12 . 0,5 + 4 . 1 = 10 km, v₂ = 4 km/h, t₀₂ = 0

X₂ = x₀₂ + v₂ (t – t₀₂) = 10 + 4t (2)

- Khi hai người gặp nhau: x₁ = x₂

\( \Rightarrow \,12t = 10 + 4t \Rightarrow t = 1,25\,h\)= 1 giờ 15 phút

Thay vào (1) \( \Rightarrow x = {x_1} = 12.1,25 = 15\,km\)

Vậy người đi xe đạp đuổi kịp người đi bộ lúc: 9 h + 1 h 15 min = 10 h 15 min

Vị trí gặp nhau cách chỗ dừng lại của người đi xe đạp là 15 km hay cách chỗ gặp trước là (15 – 6) = 9 km.

Bài 39: Một người đi từ A đến B theo chuyển động thẳng. Nửa đoạn đường đầu người ấy đi với vận tốc trung bình 16 km/h. Trong nửa còn lại người ấy đi một nửa thời gian với vận tốc 10 km/h và sau đi bộ với vận tốc 4 km/h. Tính vận tốc trung bình trên cả đoạn đường?

Lời giải

Gọi chiều dài quãng đường AB là S
Thời gian đi hết nửa đoạn đường đầu là: \({t_1} = \frac{{S{}_1}}{{{v_1}}} = \frac{S}{{2.16}} = \frac{S}{{32}}\,(h)\)
Vận tốc trung bình trên đoạn đường còn lại

\(v = \frac{{s{}_2 + {s_3}}}{{{t_2} + {t_3}}} = \frac{{{v_2}.\frac{t}{2} + {v_3}.\frac{t}{2}}}{{\frac{t}{2} + \frac{t}{2}}} = \frac{{10.\frac{t}{2} + 4.\frac{t}{2}}}{t} = 7\left( {km/h} \right)\)

Thời gian đi trên nửa quãng đường còn lại là

\({t_2} = \frac{S}{{2v}} = \frac{S}{{14}}\,(h)\)

Vận tốc trung bình của người đó trên cả đoạn đường AB là:

\({v_{tb}} = \frac{{\frac{S}{2} + \frac{S}{2}}}{{\frac{S}{{32}} + \frac{S}{{14}}}} = 9,74\,(km/h)\)

Bài 40: Vật đặt trên đỉnh dốc dài 165 m, hệ số ma sát $\mu =0,2$, góc nghiêng của dốc là $\alpha$.

a. Với giá trị nào của \(\alpha \) để vật nằm yên không trượt?

b. Cho \(\alpha  = {30^0}\). Tìm thời gian vật xuống dốc và vận tốc vật ở chân dốc? Cho tan 11⁰ = 0,2; cos 30⁰ = 0,85.

Lời giải

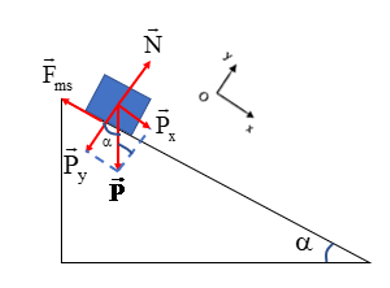
a. Để vật nằm yên không trượt thì

\({F_{ms}} \ge {P_x} \Rightarrow \mu .{P_y} \ge {P_x} \Leftrightarrow \mu .P.cos\alpha  \ge P.\sin \alpha \)

\( \Rightarrow \mu  \ge \frac{{\sin \alpha }}{{cos\alpha }} = \tan \alpha  \Rightarrow \alpha  \le \arctan \left( {0,2} \right) = {11^0}\)

b. Chọn hệ trục Oxy như hình vẽ

Vật trượt xuống dốc, theo định luật II Newton ta có

\[\left\{ {\begin{array}{*{20}{c}}{0x:{P_x} - {F_{ms}} = m.a}\\{0y:N - {P_y} = 0}\end{array}} \right.\]

\( \Rightarrow P.\sin \alpha  - \mu .P.cos\alpha  = m.a \Rightarrow a = \frac{{P.\sin \alpha  - \mu .P.cos\alpha }}{m} = g(\sin \alpha  - \mu cos\alpha )\)

Thay số ta được: a = 10.(sin30⁰ – 0,2.cos30⁰) = 3,3 m/s²

Thời gian vật xuống dưới chân dốc là

S = 0,5.a.t² \( \Rightarrow t = \sqrt {\frac{{2S}}{a}}  = \sqrt {\frac{{2.165}}{{3,3}}}  = 10s\)

Vận tốc của vật khi xuống tới chân dốc là

v = a. t = 3,3 . 10 = 33 m/s.

Bài 41: Một vật có khối lượng m = 3 kg treo vào điểm chính giữa của sợi dây thép AB. Biết AB = 4 m; CD = 10 cm; cho g = 9,8 m/s². Tính lực kéo mỗi nửa sợi dây?

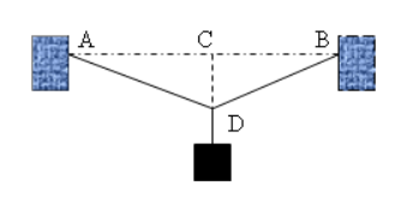
Lời giải

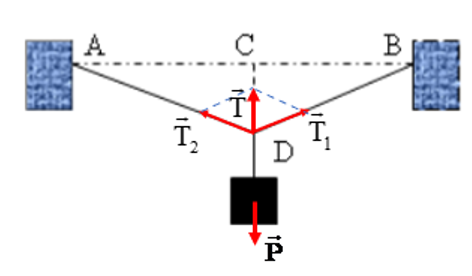
\(\Delta DAB\) cân tại D có đường trung trực DC trùng với giá của trọng lực \(\vec P\) tác dụng lên vật.

Vật nằm cân bằng nên ta có: \(\vec P + {\vec T_1} + {\vec T_2} = 0\)

\( \Rightarrow \vec P + \vec T = 0 \Rightarrow P = T\) = m.g = 3. 9,8 = 29,4 N

Do vật được treo vào điểm chính giữa của sợi dây nên T₁ = T₂

Ta có \(T = 2{T_1}.\cos \widehat {ADC} \Rightarrow {T_1} = \frac{T}{{2.\cos \widehat {ADC}}} = \frac{{29,4}}{{2.\frac{{0,1}}{{\sqrt {0,{1^2} + {2^2}} }}}} = 294,4N\)

Vậy lực kéo mỗi nửa sợi dây là 294,4 N.

Bài 42: Cho mạch điện: U = 16V , R₀ =4 Ω , R₁ = 12 Ω, R_x là giá trị tức thời của một biến trở đủ lớn, ampe kế A và dây nối có điện trở không đáng kể.

1. Tính R_x sao cho công suất tiêu thụ trên nó bằng 9 W và tính hiệu suất của mạch điện. Biết rằng tiêu hao năng lượng trên R₁, R_x là có ích, trên R₀ là vô ích.

2. Với giá trị nào của R_x thì công suất tiêu thụ trên nó là cực đại? Tính công suất ấy?

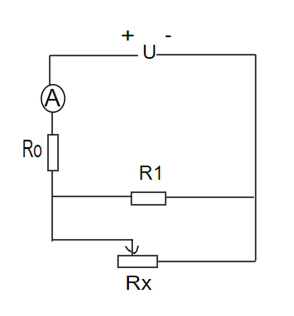
Lời giải

Mạch: \({R_0}nt\left( {{R_1}//R{}_x} \right)\)

Đặt R_x = x \(\left( \Omega  \right)\)

\({R_{td}} = {R_0} + \frac{{{R_1}.x}}{{{R_1} + x}} = 4 + \frac{{12x}}{{12 + x}} = \frac{{16x + 48}}{{12 + x}}\)

\( \Rightarrow I = \frac{U}{{{R_{td}}}} = \frac{{16}}{{\frac{{16x + 48}}{{12 + x}}}} = \frac{{12 + x}}{{x + 3}}\)

\({U_{Rx}} = U{}_{R1} = U{}_{R1x} = \frac{{12 + x}}{{x + 3}}.\frac{{12x}}{{12 + x}} = \frac{{12x}}{{x + 3}}\)

Mà \(P = \frac{{U_{Rx}^2}}{{{R_x}}} = 9W \Leftrightarrow \frac{{\frac{{144{x^2}}}{{{{\left( {x + 3} \right)}^2}}}}}{x} = 9 \Rightarrow 9{x^2} - 90x + 81 = 0\)

\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 1 \Rightarrow {R_x} = 1\left( \Omega  \right)}\\{x = 9 \Rightarrow {R_x} = 9\left( \Omega  \right)}\end{array}} \right.\)

Hiệu suất của mạch điện

\(H = \frac{{{P_{1x}}}}{P}.100\%  = \frac{{{I^2}.{R_{1x}}}}{{{I^2}.{R_{td}}}}.100\%  = \frac{{{R_{1x}}}}{{{R_{td}}}}.100\%  = \frac{{3{R_x}}}{{4{R_x} + 12}}.100\% \)

+ R_x = 1\(\left( \Omega  \right)\) \( \Rightarrow H = 18,75\% \)

+ R_x = 9\(\left( \Omega  \right)\)\( \Rightarrow H = 56,25\% \)

b. Từ câu a

\( \Rightarrow {P_{{R_x}}} = \frac{{{U^2}}}{{{R_x}}} = \frac{{{{\left( {\frac{{12x}}{{x + 3}}} \right)}^2}}}{x} = \frac{{144x}}{{{x^2} + 6x + 9}} = \frac{{144}}{{x + \frac{9}{x} + 6}}\)

Để P_Rx max khi \((x + \frac{9}{x} + 6)\,\,\min \)\( \Rightarrow \left( {x + \frac{9}{x}} \right)\,\,\min \)

Áp dụng BĐT Cô – si: \(x + \frac{9}{x} \ge 2\sqrt {x.\frac{9}{x}}  = 6\)

\( \Rightarrow {P_{Rx\,max}} = \frac{{144}}{{6 + 6}} = 12\,\left( W \right)\)

Bài 43: Cho mạch điện sau:

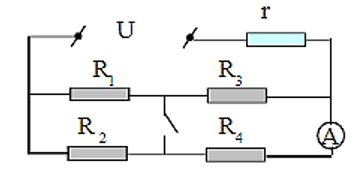
Cho U = 6 V, r = \(1\,\Omega \) = R₁; R₂ = R₃ = \(3\,\Omega \). Biết số chỉ trên A khi K đóng bằng \(\frac{9}{5}\) số chỉ của A khi K mở. Tính:

a. Điện trở R₄?

b. Khi K đóng, tính I_K?

Lời giải

- Khi K mở, mạch ngoài: \(\left( {{R_1}\,nt\,\,{R_3}} \right)//\left( {{R_2}\,nt\,\,{R_4}} \right)\)

Điện trở toàn mạch là: \({R_{tm}} = r + \frac{{\left( {{R_1} + {R_3}} \right).\left( {{R_2} + {R_4}} \right)}}{{{R_1} + {R_2} + {R_3} + {R_4}}} = 1 + \frac{{4.\left( {3 + {R_4}} \right)}}{{7 + {R_4}}} = \frac{{19 + 5{R_4}}}{{7 + {R_4}}}\)

Cường độ dòng điện trong mạch chính là

\(I = \frac{U}{{{R_{tm}}}} = \frac{{U\left( {7 + {R_4}} \right)}}{{19 + 5{R_4}}}\)

Hiệu điện thế giữa hai điểm A và B là

\({U_{AB}} = I.{R_N} = \frac{{U\left( {7 + {R_4}} \right)}}{{19 + 5{R_4}}}.\frac{{4\left( {3 + {R_4}} \right)}}{{7 + {R_4}}} = \frac{{4U\left( {3 + {R_4}} \right)}}{{19 + 5{R_4}}}\)

Số chỉ ampe kế khi k mở là

\({I_A} = \frac{{{U_{AB}}}}{{{R_2} + {R_4}}} = \frac{{4U\left( {3 + {R_4}} \right)}}{{\left( {19 + 5{R_4}} \right).\left( {3 + {R_4}} \right)}} = \frac{{4U}}{{19 + 5{R_4}}}\)

- Khi K đóng, mạch: \(\left( {{R_1}\,//\,{R_2}} \right)\,\,nt\,\,\left( {{R_3}\,//\,\,{R_4}} \right)\)

Điện trở toàn mạch là

$\begin{array}{l}{R}_{tm}^{\text{'}}=r+R_{12}+R_{34}\\ =r+\frac{R_1.R_2}{R_1+R_2}+\frac{R_3.R_4}{R_3+R_4}\\ =1+\frac{1.3}{1+3}+\frac{3.R_4}{3+R_4}=\frac{21+19R_4}{4.\left(3+R_4\right)}\end{array}$

Cường độ dòng điện trong mạch chính là

\(I' = \frac{U}{{R{'_{tm}}}} = \frac{{4U\left( {3 + {R_4}} \right)}}{{21 + 19{R_4}}}\)

Hiệu điện thế giữa hai điểm A và B là

\(U{'_{AB}} = I.R{'_N} = \frac{{4U\left( {3 + {R_4}} \right)}}{{21 + 19{R_4}}}.\frac{{9 + 6{R_4}}}{{4.\left( {3 + {R_4}} \right)}} = \frac{{U\left( {9 + 6{R_4}} \right)}}{{21 + 19{R_4}}}\)

Mà I’ = I’₁₂ = I’₃₄ = I’₃ + I’₄, I’₄ = I’_A, U’₃ = U’₄ = U’₃₄

U’₃₄ = I₃₄ . R₃₄ = \(\frac{{4U\left( {3 + {R_4}} \right)}}{{21 + 19{R_4}}}.\frac{{3{R_4}}}{{3 + {R_4}}} = \frac{{12UR{}_4}}{{21 + 19{R_4}}}\)

Số chỉ ampe kế khi k đóng là

\(I{'_A} = \frac{{U{'_4}}}{{{R_4}}} = \frac{{12U{R_4}}}{{\left( {21 + 19{R_4}} \right){R_4}}} = \frac{{12U}}{{21 + 19{R_4}}}\)

Theo đề bài thì \(I'{}_A = \frac{9}{5}{I_A} \Leftrightarrow \frac{{12U}}{{21 + 19{R_4}}} = \frac{9}{5}.\frac{{4U}}{{19 + 5{R_4}}}\)

\( \Rightarrow \frac{1}{{21 + 19{R_4}}} = \frac{3}{{5\left( {19 + 5{R_4}} \right)}} \Rightarrow {R_4} = 1\,\Omega \)

b. Khi K đóng thay R₄ vào ta tính được

I’ = 2,4 A = I’₁₂; I’_A = 1,8 A;

\( \Rightarrow U{'_{12}} = I{'_{12}}.{R_{12}} = 2,4.\frac{3}{4} = 1,8V\)

\( \Rightarrow I{'_2} = \frac{{U{'_{12}}}}{{{R_{12}}}} = \frac{{1,8}}{3} = 0,6A\)

Mà I’₂ + I_K = I’₄ = I’_A \( \Rightarrow {I_K} = I{'_A} - I{'_2} = 1,8 - 0,6 = 1,2A\)

Bài 44: Một vật được ném từ một điểm M ở độ cao h = 45 m với vận tốc ban đầu v_o = 20 m/s lên trên theo phương hợp với phương nằm ngang một góc 45⁰. Lấy g = 10 m/s², bỏ qua lực cản của không khí. Hãy xác định:

a. Quỹ đạo của vật, độ cao cực đại vật đạt đươc so với mặt đất và thời gian vật bay trong không khí.

b. Tầm bay xa của vật, vận tốc của vật khi chạm đất.

c. Xác định thời gian để vật có độ cao 50 m và xác định vận tốc của vật khi đó.

Lời giải

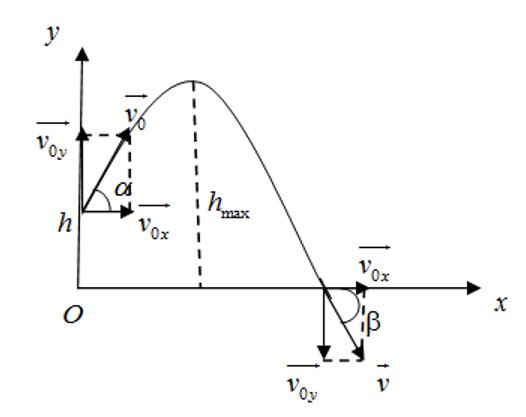
a. Chọn hệ quy chiếu Oxy như hình vẽ, gốc thời gian là lúc khảo sát vật.

Chiếu lên trục ox có:

\[\left\{ \begin{array}{l}\begin{array}{*{20}{c}}{{x_0} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\\begin{array}{l}{v_{0x}} = {v_0}.cos\alpha  = 20.cos{45^0} = 10\sqrt 2 \left( {m/s} \right)\\{a_x} = 0\end{array}\end{array}\\{v_x} = 10\sqrt 2 \left( {m/s} \right)\end{array} \right.\]

\( \Rightarrow x = 10\sqrt 2 .t\,\,(m)\)

Chiếu lên trục oy có:

\[\left\{ \begin{array}{l}\begin{array}{*{20}{c}}{{y_0} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\\begin{array}{l}{v_{0y}} = {v_0}.\sin \alpha  = 20.\sin {45^0} = 10\sqrt 2 \left( {m/s} \right)\\{a_y} =  - g =  - 10\,m/{s^2}\end{array}\end{array}\\{v_y} = 10\sqrt 2  - 10t\end{array} \right.\]

\( \Rightarrow y = 45 + 10\sqrt 2 t - 5{t^2}\,\,(m)\)

Phương trình quỹ đạo của vật là: \(y = 45 + x - \frac{{{x^2}}}{{40}}\)

\( \Rightarrow \) Vật có quỹ đạo là một Parabol

Khi lên đến độ cao max thì: 

v­_y = 0 \( \Rightarrow 10\sqrt 2  - 10t = 0 \Rightarrow t = \sqrt 2 \,(s)\)

Độ cao vật đạt được là: \(H = 45 + 10\sqrt 2 .\sqrt 2  - 5.{\left( {\sqrt 2 } \right)^2} = 55\,\,(m)\)

Khi vật chạm đất thì y = 0

\( \Rightarrow 45 + 10\sqrt 2 t - 5{t^2} = 0\,\, \Rightarrow t = 4,73\,s\)

Vậy sau 4,73s thì vật chạm đất

b. Tầm xa của vật: L = x = \(10\sqrt 2 .4,73 = 66,89\,(m)\)

Vận tốc vật khi chạm đất:

\(v = \sqrt {v_x^2 + v_y^2}  = \sqrt {{{\left( {10\sqrt 2 } \right)}^2} + {{\left( {10\sqrt 2  - 10.4,73} \right)}^2}}  = 36,05\,(m/s)\)

 c. Khi vật có độ cao 50 m thì

\(45 + 10\sqrt 2 t - 5{t^2} = 50\)

\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{{t_1} = 0,414\,(s) \Rightarrow {v_{y1}} = 10\sqrt 2  - 10.0,414 \approx 10m/s}\\{{t_2} = 2,414\,(s) \Rightarrow {v_{y2}} = 10\sqrt 2  - 10.2,414 \approx  - 10m/s}\end{array}} \right.\)

Tại t₁ vật đang đi lên, t₂ vật đang đi xuống.

Bài 45: Một xe đạp đi từ A đến B nửa quãng đường đầu, xe đi với vận tốc 20 km/h nửa còn lại đi với vận tốc 30 km/h. Hỏi vận tốc trung bình của xe đạp trên cả quãng đường là

Lời giải

Vận tốc trung bình của xe đạp trên cả quãng đường là

\({v_{tb}} = \frac{{\frac{S}{2} + \frac{S}{2}}}{{\frac{S}{{2{v_1}}} + \frac{S}{{2{v_2}}}}} = \frac{1}{{\frac{1}{{2.20}} + \frac{1}{{2.30}}}} = 24km/h\)

Bài 46: Trong khoảng thời gian liên tiếp bằng nhau 4 s, chất điểm chuyển động thẳng nhanh dần đều đi được những quãng đường lần lượt là 24 m và 64 m. Tính vận tốc ban đầu và gia tốc của chất điểm.

Lời giải

Áp dụng công thức: \(s = {v_o}.t + \frac{1}{2}.a.{t^2}\)

Quãng đường đi được trong 4 giây đầu là:

\({s_1} = 4{v_o} + 8a = 24m\,(1)\)

Quãng đường đi được trong 8 giây là

\(s = {s_1} + {s_2} = 24 + 64 = 88 = 8{v_o} + 32a = (2)\)

Từ (1) và (2), ta được: v₀ = 1 m/s, a = 2,5 m/s²

Bài 47: Một vật rơi tự do trong giây cuối rơi được 35 m. Tính thời gian từ lúc bắt đầu rơi tới khi chạm đất.

Lời giải

Gọi t là thời gian vật rơi tới khi chạm đất

Quãng đường vật rơi trong thời gian t là

\({S_t} = \frac{1}{2}g{t^2}\)

Quãng đường vật rơi trong thời gian (t – 1) là

\({S_{t - 1}} = \frac{1}{2}g{\left( {t - 1} \right)^2}\)

Trong giây cuối vật rơi được 35 m

\(S{}_t - {S_{t - 1}} = \frac{1}{2}g.{t^2} - \frac{1}{2}g.{\left( {t - 1} \right)^2} = 35m\)

\( \Rightarrow 5{t^2} - 5{\left( {t - 1} \right)^2} = 35 \Rightarrow 10t - 5 = 35 \Rightarrow t = 4s\)

Bài 48: Một vật chuyển động thẳng nhanh dần đều có vận tốc đầu là 18 km/h. Trong giây thứ năm, vật đi được quãng đường là 5,9 m.

a. Tính gia tốc của vật.

b. Tính quãng đường vật đi được sau khoảng thời gian là 10 s kể từ khi vật bắt đầu chuyển động.

Lời giải

a. Quãng đường vật đi được sau 4 s là

\({s_4} = 4{v_0} + 8a\)

Quãng đường vật đi được sau 5 s là

\({s_5} = 5{v_0} + 12,5a\)

Quãng đường vật đi được trong giây thứ 5 là

\(\Delta s = {s_5} - {s_4} = {v_0} + 4,5a = 5,9\)

\( \Rightarrow a = \frac{{5,9 - 5}}{{4,5}} = 0,2\,m/{s^2}\)

b. Quãng đường vật đi được sau 10 s là

\({s_{10}} = 10.5 + \frac{1}{2}.0,{2.10^2} = 60\,m\)

Bài 49: Người ta kéo một cái thùng 30 kg trượt đều trên sàn nhà với vận tốc 1,5m/s bằng một dây hợp với phương nằm ngang một góc 45⁰, lực tác dụng lên dây là 150 N. Tính công và công suất của lực kéo khi thùng trượt được 15 m.

Lời giải

Công của lực kéo là

\(A = F.s.cos\alpha  = 150.15.cos{45^0} \approx 1591J\)

Công suất thực hiện là

\(P = \frac{A}{t} = F.v = 150.1,5 = 225\,\,W\)

Bài 50: Một bóng đèn có ghi 220V – 40W. Mắc bóng đèn này vào nguồn điện 220V.

a. Tính điện trở của đèn và nói rõ sự chuyển hoá năng lượng khi đèn hoạt động.

b. Tính công suất tiêu thụ của đèn và điện năng tiêu thụ của nó trong 5 phút. Đèn có sáng bình thường không. Vì sao?

Lời giải

a. Điện trở của đèn là

\(R = \frac{{{U^2}}}{P} = \frac{{{{220}^2}}}{{40}} = 1210\left( \Omega  \right)\)

Khi đèn hoạt động thì điện năng chuyển hóa thành quang năng và nhiệt năng.

b. Khi mắc đèn vào nguồn điện 220 V, hiệu điện thế qua đèn bằng hiệu điện thế định mức của đèn, đèn sáng bình thường.

\( \Rightarrow \)Công suất tiêu thụ của đèn bằng công suất định mức bằng 40 W.

Điện năng tiêu thụ trong 5 phút = 5 . 60 = 300 s là

A = P . t = 40 . 300 = 12000 (J)

Bài 51: Một vật khối lượng m = 1 kg được kéo chuyển động ngang bởi một lực $\overrightarrow{F}$ hợp với phương ngang một góc $\alpha$= 30° và có độ lớn F = 2 N. Biết khi bắt đầu chuyển động được 2 s vật đi được quãng đường 1,66 m. Cho g = 10 m/s², \(\sqrt 3  = 1,73\).

a, Tính hệ số ma sát trượt giữa vật và mặt sàn.

b, Tính hệ số ma sát với lực kéo nói trên vật chuyển động thẳng đều.

Lời giải

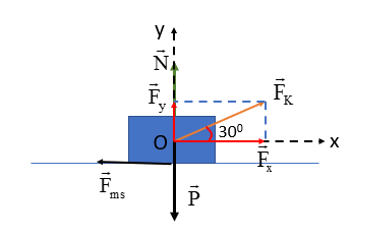
Chọn hệ trục Oxy như hình vẽ.

Vật chịu tác dụng của các lực \(\vec F,\,{\vec F_{ms}},\vec N,\,\vec P\)

Theo định luật II Newton, ta có: \(\vec F + {\vec F_{ms}} + \vec N + \vec P = m.\vec a\)

Chiếu lần lượt lên Ox, Oy, ta được:

\(\left\{ {\begin{array}{*{20}{c}}{{F_x} - {F_{ms}} = m.a \Rightarrow {F_x} - \mu .N = m.a\,(1)}\\{{F_y} + N - P = 0 \Rightarrow N = P - F{}_y\,(2)}\end{array}} \right.\)

Thay (2) vào (1), được:

\(F.cos{30^0} - \mu \left( {P - F.\sin {{30}^0}} \right) = m.a\,\,\left( 3 \right)\)

Lại có: \(s = {v_0}.t + \frac{1}{2}a.{t^2} \Rightarrow a = \frac{{2s}}{{{t^2}}} = \frac{{2.1,66}}{{{2^2}}} = 0,83\,m/{s^2}\)

Thay vào (3) \( \Rightarrow \mu  = \frac{{F.cos{{30}^0} - m.a}}{{P - F.\sin {{30}^0}}} = \frac{{2.\frac{{\sqrt 3 }}{2} - 1.0,83}}{{1.10 - 2.0,5}} \approx 0,1\)

b. Khi vật chuyển động thẳng đều thì a = 0

\( \Rightarrow \mu  = \frac{{F.cos{{30}^0} - m.a}}{{P - F.\sin {{30}^0}}} = \frac{{2.\frac{{\sqrt 3 }}{2} - 1.0}}{{1.10 - 2.0,5}} \approx 0,192\)

Bài 52: Một người dự định đi bộ với vận tốc 5 km/h nhưng đi đến đúng nửa đường thì nhờ bạn đèo xe đạp đi tiếp với vận tốc 12 km/h, do đó đã đến sớm hơn đự định 28 phút. Hỏi người ấy đã đi hết toàn bộ quãng đường mất bao lâu?

Lời giải

Gọi s₁, t₁ là quãng đường, thời gian người đi bộ, s₂, t₂ là quãng đường, thời gian đi xe đạp; s là tổng quãng đường người phải đi.

Đổi 28 phút = \(\frac{7}{{15}}\,(h)\)

Ta có: \(\left\{ {\begin{array}{*{20}{c}}{{s_1} = {s_2} \Rightarrow 5{t_1} = 12{t_2} \Rightarrow {t_2} = \frac{5}{{12}}{t_1}}\\{{s_1} + {s_2} = s \Rightarrow 5{t_1} + 12{t_2} = 5({t_1} + {t_2} + \frac{7}{{15}})}\end{array}} \right.\)

\( \Rightarrow {t_1} = \frac{4}{5}\,(h) \Rightarrow {t_2} = \frac{5}{{12}}.\frac{4}{5} = \frac{1}{3}(h)\)

Người đó đã đi hết toàn bộ quãng đường mất thời gian là

t = t₁ + t₂ = \(\frac{4}{5} + \frac{1}{3} = \frac{{17}}{{15}}\,(h) \approx 1,13\,(h)\)

Bài 53: Một người dự định đi bộ một quãng đường với vận tốc không đổi 5 km/h nhưng đi đến đúng nửa đường thì nhờ được bạn đèo xe đạp đi tiếp với vận tốc không đổi 12 km/h, do đó đến sớm dự định 28 phút. Hỏi thời gian dự định đi lúc đầu là bao nhiêu?

Lời giải

Gọi s₁, t₁ là quãng đường, thời gian người đi bộ, s₂, t₂ là quãng đường, thời gian đi xe đạp; s là tổng quãng đường người phải đi.

Đổi 28 phút = \(\frac{7}{{15}}\,(h)\)

Ta có: \(\left\{ {\begin{array}{*{20}{c}}{{s_1} = {s_2} \Rightarrow 5{t_1} = 12{t_2} \Rightarrow {t_2} = \frac{5}{{12}}{t_1}}\\{{s_1} + {s_2} = s \Rightarrow 5{t_1} + 12{t_2} = 5({t_1} + {t_2} + \frac{7}{{15}})}\end{array}} \right.\)

\( \Rightarrow {t_1} = \frac{4}{5}\,(h) \Rightarrow {t_2} = \frac{5}{{12}}.\frac{4}{5} = \frac{1}{3}(h)\)

Thời gian dự định đi lúc đầu là

t = t₁ + t₂ + \(\frac{7}{{15}}\,\)= \(\frac{4}{5} + \frac{1}{3} + \frac{7}{{15}} = \frac{8}{5}\,(h) \approx 1,6\,(h)\)

Bài 54: Tại hai điểm A và B trên mặt nước có hai nguồn sóng giống nhau với biên độ a, bước sóng là 10 cm. Điểm N cách A một khoảng 25 cm, cách B một khoảng 10 cm sẽ dao động với biên độ là

A. 2a.           B. a.             C. – 2a.        D. 0.

Lời giải

Đáp án đúng: D

Hai nguồn sóng giống nhau tức là có độ lệch pha △φ = 0.

Biên độ sóng tại N là

\({A_N} = 2a\left| {cos\left( {\pi \frac{{NB - NA}}{\lambda }} \right)} \right| = 2a\left| {cos\left( {\pi \frac{{10 - 25}}{{10}}} \right)} \right| = 2a\left| {cos\frac{{\left( { - 3\pi } \right)}}{2}} \right| = 0\)

Bài 55: Tại hai điểm A, B trên mặt nước có hai nguồn dao động cùng pha với cùng tần số f = 12 Hz. Tại điểm M cách các nguồn A, B những đoạn d₁ = 18 cm, d₂ = 24 cm sóng có biên độ cực đại. Giữa M và đường trung trực của AB có hai đường cong cực đại khác. Vận tốc truyền sóng trên mặt nước là

A. 24 cm/s.

B. 26 cm/s.

C. 28 cm/s.

D. 20 cm/s.

Lời giải

Đáp án đúng: A

Ta có M là một cực đại mà giữa M và trung trực của AB còn có 2 đường cực đại khác

\( \Rightarrow \) M thuộc cực đại bậc 3 (k = 3)

\( \Rightarrow {d_2} - {d_1} = k\lambda  \Rightarrow \lambda  = \frac{{{d_2} - {d_1}}}{k} = \frac{{24 - 18}}{3} = 2\left( {cm} \right)\)

Vận tốc truyền sóng là \(v = \lambda f = 2.12 = 24\left( {cm/s} \right)\)

Bài 56: Một bóng đèn được nối với nguồn 120V. Năng lượng mà nguồn cung cấp cho đèn trong 1 phút là 1800 J. Cường độ dòng điện chạy qua đèn là

A. 0,25 A.

B. 0,5 A.

C. 0,75 A.

D. 1 A.

Lời giải

Đáp án đúng: A

Cường độ dòng điện chạy qua đèn là

\(I = \frac{A}{{U.t}} = \frac{{1800}}{{120.1.60}} = 0,25A\)

Bài 57: Một bóng đèn có dòng điện chạy qua là 500 mA khi nối với nguồn 120 V. Năng lượng mà nguồn cung cấp cho đèn trong 5 phút là

A. 300 J.

B. 9000 J.

C. 18000 J.

D. 180000 J.

Lời giải

Đáp án đúng: C

Năng lượng mà nguồn cung cấp cho đèn trong 5 phút là

A = U. I. t = 120 . 0,5 . 5 . 60 = 18000 J

Bài 58: Một vật làm bằng kim loại nếu bỏ vào bình chứa có vạch chia thể tích thì làm cho nước trong bình dâng lên thêm 100 cm³ nếu treo vật vào một lực kế thì lực kế chỉ 7,8 N, cho trọng lượng riêng của nước bằng 10000 N/m³.

a. Tính lực đẩy Ác - si - mét tác dụng lên vật.

b. Xác định khối lượng riêng của chất làm lên vật.

Lời giải

a. Thể tích nước dâng lên bằng thể tích của vật: V = 100 cm³ = 10^-4 m³

Lực đẩy Ác - si - mét tác dụng lên vật là

F_A = d. V = 10000 . 10^-4 = 1 N

b. Số chỉ của lực kế chính là trọng lượng của vật: P = 7,8 N

Khối lượng riêng của chất làm lên vật là

\(D = \frac{d}{{10}} = \frac{P}{{10.V}} = \frac{{7,8}}{{{{10.10}^{ - 4}}}} = 7800kg/{m^3}\)

Bài 59: Một vật bằng kim loại, nếu bỏ vào bình chứa có vạch chia thể tích thì làm cho nước trong bình dâng lên thêm 50 cm³. Nếu treo vật vào một lực kế thì lực kế chỉ 3,9 N. Cho biết trọng lượng riêng của nước là 10000 N/m³.

a. Tính lực đẩy Ác-si-mét tác dụng lên vật.

b. Xác định khối lượng riêng của chất làm lên vật.

Lời giải

a. Thể tích nước dâng lên bằng thể tích của vật: V = 50 cm³ = 5.10^-5 m³

Lực đẩy Ác - si - mét tác dụng lên vật là

F_A = d. V = 10000 . 5. 10^-5 = 0,5 N

b. Số chỉ của lực kế chính là trọng lượng của vật: P = 3,9 N

Khối lượng riêng của chất làm lên vật là

\(D = \frac{d}{{10}} = \frac{P}{{10.V}} = \frac{{3,9}}{{{{10.5.10}^{ - 5}}}} = 7800kg/{m^3}\)

Bài 60: Hai gương phẳng G₁, G₂ quay mặt phản xạ vào nhau và tạo với nhau một góc 60⁰. Một điểm S nằm trong khoảng 2 gương.

a. Hãy nêu cách vẽ đường đi của tia sáng phát ra từ S phản xạ lần lượt qua G₁, G₂ rồi quay trở lại S.

b. Tính góc tạo bởi tia xuất phát từ S và tia phản xạ đi qua S.

Lời giải

a.

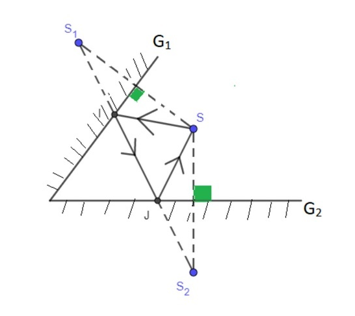
Cách vẽ:

- Lấy S₁ đối xứng S qua gương G₁ (S₁ là ảnh của S qua gương G₁).

- Lấy S₂ đối xứng S qua gương G₂ (S₂ là ảnh của S qua gương G₂).

- Nối S₁ với S₂ cắt gương G₁ tại I và cắt gương G₂ tại J.

- Nối S, I, J ta được đường của tia sáng phát ra từ S phản xạ lần lượt qua G₁, G₂ rồi quay trở lại S.

b.

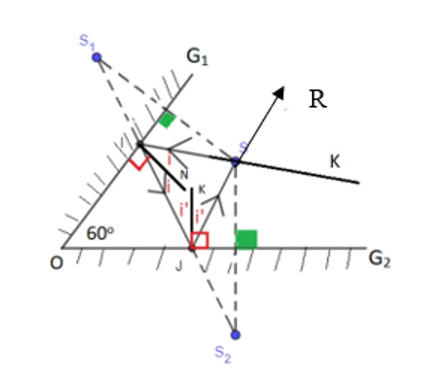
b. Kẻ pháp tuyến IN và JK

Xét tứ giác OISJ có:

\[\widehat {OIS} + \widehat {ISJ} + \widehat {SJO} + \widehat {IOJ} = 360{}^0\]

\( \Rightarrow {90^0} + i + \widehat {ISJ} + {90^0} + i' + {60^0} = {360^0}\)

\( \Rightarrow i + i' + \widehat {ISJ} = {120^0}\) (1)

Xét tam giác OIJ có:

\[\widehat {OIJ} + \widehat {IJO} + \widehat {IOJ} = {180^0}\]

\( \Rightarrow {90^0} - i + {90^0} - i' + {60^0} = {180^0}\)

\( \Rightarrow i + i' = {60^0}\) (2)

Thay (2) vào (1), được \(\widehat {ISJ} = {120^0} - {60^0} = {60^0}\)

Góc tạo bởi tia tới xuất phát từ S và tia phản xạ đi qua S là

\(\widehat {ISR} = {180^0} - {60^0} = {120^0}\)

Bài 61: Cho mạch điện hình vẽ:

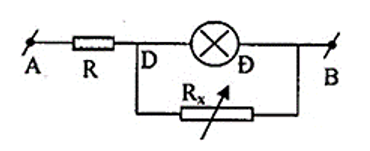
Biết $R=4\Omega$, đèn Đ ghi 6 V – 3 W, U_AB = 9 V không đổi, R_x là biến trở. Điện trở của đèn không đổi. Xác định giá trị của R_x để đèn sáng bình thường.

A. \(12\Omega \).

B. \(6\Omega \).

C. \(24\Omega \).

D. \(9\Omega \).

Lời giải

Đáp án đúng: C

Vì đèn sáng bình thường nên U_DB = U_Đ = U_Rx= 6 V.

Mà U_AB = U_AD + U_DB \( \Rightarrow {U_{AD}} = 9 - 6 = 3V\)

Cường độ dòng điện mạch chính là

\(I = {I_{DB}} = {I_R} = {I_{AD}} = \frac{{{U_{AD}}}}{R} = \frac{3}{4} = 0,75A\)

Cường độ dòng điện chạy qua bóng đèn là

I_Đ = \(\frac{P}{U} = \frac{3}{6} = 0,5A\)

Cường độ dòng điện qua biến trở là

I_Rx = I – I_Đ­ = 0,75 – 0,5 = 0,25 A

Điện trở của biến trở là \({R_x} = \frac{{{U_{Rx}}}}{{{I_{Rx}}}} = \frac{6}{{0,25}} = 24\Omega \)

Bài 62: Cho mạch điện như hình vẽ. Biết U_AB = 90 V;$R_1=R_3=45\Omega ;R_2=90\Omega$. Tìm R₄. Biết khi K mở và khí K đóng cường độ dòng điện qua R₄ là như nhau.

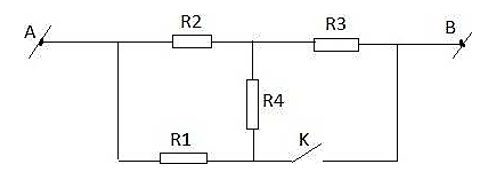
Lời giải

- Khi K mở mạch trở thành: (R₂ // (R₁ nt R₄)) nt R₃

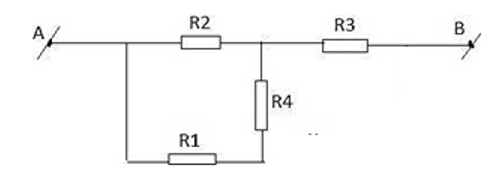
R₁₄ = R₁ + R₄ = 45 + R₄

\({R_{124}} = \frac{{{R_2}.\left( {45 + {R_4}} \right)}}{{{R_2} + 45 + {R_4}}} = \frac{{90\left( {45 + {R_4}} \right)}}{{135 + {R_4}}}\)

\({R_{1234}} = {R_3} + {R_{124}} = 45 + \frac{{90\left( {45 + {R_4}} \right)}}{{135 + {R_4}}} = \frac{{10125 + 135{R_4}}}{{135 + {R_4}}}\)

Lại có:

I = I₃ = I₁₂₄ = \(\frac{{{U_{AB}}}}{{R{}_{1234}}} = \frac{{90\left( {135 + {R_4}} \right)}}{{10125 + 135{R_4}}}\)

I₁₂₄ = I₂ + I₁₄ \( \Rightarrow {I_1} = {I_4} = {I_{14}} = {I_{124}} - {I_2}\)

Mà U₂ = U₁₄ = U₁₂₄

Nên \({I_4} = {I_{124}} - \frac{{{U_{124}}}}{{{R_2}}} = {I_{124}} - \frac{{{I_{124}}.{R_{124}}}}{{{R_2}}} = {I_{124}}\left( {1 - \frac{{{R_{124}}}}{{{R_2}}}} \right)\)

\[ \Rightarrow {I_4} = \frac{{90\left( {135 + {R_4}} \right)}}{{10125 + 135{R_4}}}\left( {1 - \frac{{90\left( {45 + {R_4}} \right)}}{{\left( {135 + {R_4}} \right).90}}} \right)\]

\( \Rightarrow {I_4} = \frac{{8100}}{{10125 + 135{R_4}}} = \frac{{180}}{{225 + 3{R_4}}}\) (1)

- Khi K đóng mạch trở thành: R­₁ // (R₂ nt (R₃ //R₄))

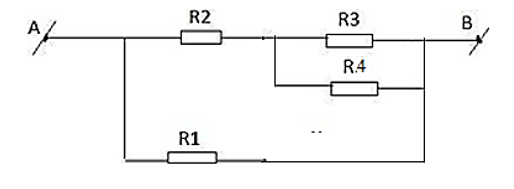
\({R_{34}} = \frac{{{R_3}.{R_4}}}{{{R_3} + {R_4}}} = \frac{{45{R_4}}}{{45 + {R_4}}}\)

\({R_{234}} = {R_2} + {R_{34}} = 90 + \frac{{45{R_4}}}{{45 + {R_4}}} = \frac{{4050 + 135{R_4}}}{{45 + {R_4}}}\)

\({R_{1234}} = \frac{{{R_1}.{R_{234}}}}{{{R_1} + {R_{234}}}} = \frac{{45.\left( {4050 + 135{R_4}} \right)}}{{\left( {45 + {R_4}} \right).\left( {45 + \frac{{4050 + 135{R_4}}}{{45 + {R_4}}}} \right)}} = \frac{{4050 + 135{R_4}}}{{135 + 4{R_4}}}\)

Ta có: U_AB = U₂₃₄ = U₁; U₂₃₄ = U₂ + U₃₄; U₃₄ = U₃ = U₄

Nên \({I_4} = \frac{{{U_4}}}{{{R_4}}} = \frac{{{U_{34}}}}{{{R_4}}} = \frac{{{U_{234}} - {U_2}}}{{{R_4}}} = \frac{{{U_{AB}} - {U_2}}}{{{R_4}}} = \frac{{{U_{AB}} - {I_2}.{R_2}}}{{{R_4}}}\)

Mà I₂ = I₂₃₄ = \(\frac{{{U_{234}}}}{{{R_{234}}}} = \frac{{{U_{AB}}}}{{{R_{234}}}}\)

\( \Rightarrow {I_4} = \frac{{{U_{A{\bf{B}}}} - \frac{{{U_{AB}}}}{{{R_{234}}}}.{R_2}}}{{{R_4}}} = \frac{{90 - \frac{{90.90}}{{{R_{234}}}}}}{{{R_4}}} = \frac{{90{R_{234}} - 8100}}{{{R_4}.{R_{234}}}}\) (*)

Thay R₂₃₄= \(\frac{{4050 + 135{R_4}}}{{45 + {R_4}}}\) vào (*) ta được:

\({I_4} = \frac{{4050}}{{4050 + 135{R_4}}}\) (2)

Vì I₄ trong 2 trường hợp là bằng nhau nên (1) = (2)

\(\frac{{180}}{{225 + 3{R_4}}}\)\( = \frac{{4050}}{{4050 + 135{R_4}}}\)\( \Rightarrow \frac{6}{{75 + {R_4}}} = \frac{{135}}{{1350 + 45{R_4}}}\)

\( \Rightarrow 8100 + 270{R_4} = 10125 + 135{R_4} \Rightarrow {R_4} = 15\Omega \)

Bài 63: Một vật sáng AB đặt cách màn chắn một khoảng L = 90 cm. Trong khoảng giữa vật sáng và màn chắn đặt một thấu kính hội tụ có tiêu cự f sao cho trục chính của thấu kính vuông góc với AB và màn. Khoảng cách giữa 2 vị trí đặt thấu kính để ảnh rõ nét trên màn chắn là l = 30 cm. Tính tiêu cự của thấu kính hội tụ. Cho biết \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\) (d là khoảng cách từ vật đến thấu kính; d’ là khoảng cách từ ảnh đến thấu kính).

A. 10 cm.

B. 20 cm.

C. 30 cm.

D. 40 cm.

Lời giải

Đáp án đúng: B

Để có được ảnh rõ nét trên màn tức là di chuyển thấu kính đến vị trí mà màn chắn hứng được ảnh thật của vật.

Ta có 2 vị trí có thể cho ảnh rõ nét là khi vật cách thấu kính một đoạn d hoặc d' = L - d sao cho thỏa mãn: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\)\( \Rightarrow f\left( {d + d'} \right) = d.d'\) (2)

Ta có: L = d + d’; l = d – d’

\( \Rightarrow {L^2} - {l^2} = {\left( {d + d'} \right)^2} - {\left( {d - d'} \right)^2} = 4.d.d'\left( 1 \right)\)

Thay (2) vào (1) được: \({L^2} - {l^2} = 4f\left( {d + d'} \right) = 4f.L\)\( \Rightarrow f = \frac{{{L^2} - {l^2}}}{{4L}}\)

Thay L = 90 cm, l = 30 cm vào (*) được: f = 20 cm.

Bài 64: Một ca nô chạy xuôi dòng sông dài 150 km. Vận tốc của ca nô khi nước không chảy là 25 km/h, vận tốc của dòng nước chảy là 5 km/h. Tính thời gian ca nô đi hết đoạn sông đó.

A. 5 h.

B. 12 h.

C. 13 h.

D. 14 h.

Lời giải

Đáp án đúng: A

Vận tốc thực của ca nô khi đi xuôi là

V = v_cano + v_nước = 25 + 5 = 30 (km/h)

Thời gian ca nô đi hết đoạn sông đó là

t = S : V = 150 : 30 = 5 h.

Bài 65: Cho mạch RLC mắc nối tiếp $R=180\Omega$, cuộn dây $r=20\Omega$, $L=\frac{2}{\pi }\left(H\right)$, $C=\frac{100}{\pi }{.10}^{-6}\left(F\right)$. Biết dòng điện trong mạch có biểu thức \(i = cos\left( {100\pi t} \right)\,(A)\). Điện áp hiệu dụng giữa hai đầu đoạn mạch là bao nhiêu?

Lời giải

Cảm kháng của cuộn dây là \({Z_L} = \omega .L = 100\pi .\frac{2}{\pi } = 200\Omega \)

Dung kháng của tụ điện là \({Z_C} = \frac{1}{{\omega .C}} = \frac{\pi }{{100\pi {{.100.10}^{ - 6}}}} = 100\Omega \)

Tổng trở: \(Z = \sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)

\( \Rightarrow Z = \sqrt {{{\left( {180 + 20} \right)}^2} + {{\left( {200 - 100} \right)}^2}}  = 100\sqrt 5 \Omega \)

Cường độ dòng điện hiệu dụng: \(I = \frac{{I{}_0}}{{\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\,(A)\)

Điện áp hiệu dụng giữa hai đầu đoạn mạch là

U = I. Z = \(\frac{1}{{\sqrt 2 }}.100\sqrt 5  = 50\sqrt {10} \left( V \right)\)

Bài 66: Hai xe I và II chuyển động trên cùng một đường thẳng tại hai điểm A và B. Biết tốc độ xe I và xe II lần lượt là 50 km/h và 30 km/h. Tính vận tốc tương đối của xe I so với xe II khi:

a) Hai xe chuyển động cùng chiều.

b) Hai xe chuyển động ngược chiều.

Lời giải

Vận tốc tương đối của xe I so với xe II là

\({\vec v_{I,II}} = {\vec v_I} - {\vec v_{II}}\) (*)

Chọn chiều dương là chiều chuyển động của xe I.

a. Khi hai xe chuyển động cùng chiều, chiếu (*) lên chiều dương, ta được

Vận tốc tương đối của xe I so với xe II là

v_{I, II} = v_I – v_II = 50 – 30 = 20 (km/h)

b. Khi hai xe chuyển động ngược chiều, chiếu (*) lên chiều dương, ta được

Vận tốc tương đối của xe I so với xe II là

v’_{I, II} = v_I – (- v_II)= 50 + 30 = 80 (km/h)

Bài 67: Tác dụng 1 lực 480 N lên pit - tong nhỏ của một máy ép thủy lực, diện tích pit - tong nhỏ là 2,5 cm²; diện tích pit - tong lớn là 200 cm². Tính áp lực tác dụng lên pit - tong lớn và tính áp suất tác dụng lên pit - tong nhỏ.

Lời giải

Gọi f₁, f₂ lần lượt là lực tác dụng lên pit – tong lớn và pit – tong nhỏ.

s₁, s₂ lần lượt là diện tích pit – tong lớn và pit – tong nhỏ.

Áp suất tác dụng lên pit – tong nhỏ là

\(p = \frac{{{f_2}}}{{{s_2}}} = \frac{{480}}{{2,{{5.10}^{ - 4}}}} = 1920000\,(Pa)\)

Ta có: \(\frac{{{f_1}}}{{{f_2}}} = \frac{{{s_1}}}{{{s_2}}}\) \( \Rightarrow {f_1} = \frac{{{f_2}.{s_1}}}{{{s_2}}}\)

Áp lực tác dụng lên pit - tong lớn là

\({f_1} = \frac{{{f_2}.{s_1}}}{{{s_2}}} = \frac{{200.480}}{{2,5}} = 38400\,(N)\)