Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Vật lí gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Vật lí. Mời các bạn đón xem:

Top 1000 câu hỏi thường gặp môn Vật lí (Phần 8)

Bài 1: Một con lắc lò xo dao động với biên độ 6 cm. Xác định li độ của vật để thế năng của vật bằng $\frac{1}{3}$ động năng của nó.

A. ± $3\sqrt{2}$cm.

B. ± 3 cm.

C. ± 2 cm.

D. ± 1 cm.

Lời giải

Đáp án đúng: B

${{W}_{d}}=3{{W}_{t}}\Rightarrow \text{W}=4{{W}_{t}}\Rightarrow x=\pm \frac{A}{2}=\pm 3cm$

Bài 2: Tại O đặt một điện tích điểm Q. Một thiết bị đo độ lớn cường độ điện trường chuyển động từ A đến C theo một đường thẳng số chỉ của nó tăng từ E đến 1,5625 E rồi lại giảm xuống E. Khoảng cách AO bằng:

A. $\frac{AC}{\sqrt{2}}$.

B. $\frac{AC}{\sqrt{3}}$.

C. $\frac{5AC}{8}$.  

D. $\frac{AC}{1,2}$.

Lời giải

Đáp án đúng: D

Từ dữ kiện bài cho ta có hình vẽ:

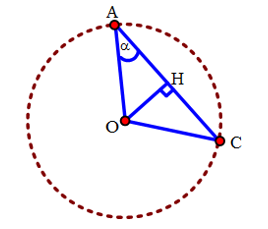
Độ lớn cường độ điện trường lớn nhất tại H là trung điểm của AC.

Độ lớn cường độ điện trường của điện tích Q gây ra tại A và H là:

$\left\{\begin{array}{l}{E}_A=\frac{k\left|Q\right|}{O{A}^2}=E\\ E_H=\frac{k\left|Q\right|}{O{H}^2}=1,5625E\end{array}\right.\iff \left\{\begin{array}{l}{E}_A=\frac{k\left|Q\right|}{O{A}^2}=E\\ E_H=\frac{k\left|Q\right|}{O{A}^2-A{H}^2}=1,5625E\end{array}\right.$

$\begin{array}{l}\left\{\begin{array}{l}{E}_A=\frac{k\left|Q\right|}{O{A}^2}=E\\ E_H=\frac{k\left|Q\right|}{O{A}^2-\frac{A{C}^2}{4}}=1,5625E\end{array}\right.\\ \Rightarrow \frac{E_A}{E_H}=\frac{1}{1,5625}=\frac{16}{25}=\frac{O{A}^2-\frac{A{C}^2}{4}}{O{A}^2}\end{array}$

$\Rightarrow OA=\frac{5}{6}AC=\frac{AC}{1,2}$

Bài 3: Đặt một điện tích thử q = - 10^-6 C tại một điểm, nó chịu một lực điện F = 10^-3 N. Tính độ lớn cường độ điện trường tại điểm đó.

Lời giải

Độ lớn cường độ điện trường tại điểm đó:

$E=\frac{F}{\left| q \right|}=\frac{{{10}^{-3}}}{{{10}^{-6}}}=1000\left( \text{V/m} \right)$

Bài 4: Một con lắc đơn dao động điều hòa tại nơi có gia tốc trọng trường g = 9,8 m/s² với chu kì T = 2 s. Quả cầu nhỏ của con lắc có khối lượng m = 50 g. Biết biên độ góc α₀ = 0,15 rad. Lấy π = 3,1416. Cơ năng dao động của con lắc bằng

A.  0,55.10^-2 J.

B. 10^-2 J.      

C.  0,993.10^-2 J.     

D. 5,5.10^-2 J.

Lời giải

Đáp án đúng: A

Ta có: $T=2\pi \sqrt{\frac{\ell }{g}}\Rightarrow \ell =\frac{{{T}^{2}}.g}{4{{\pi }^{2}}}=\frac{{{2}^{2}}.9,8}{4{{\pi }^{2}}}=1\left( m \right)$

Cơ năng của con lắc là:

\[\text{W}=\frac{1}{2}mg\ell \alpha _{0}^{2}=5,{{5.10}^{-3}}\left( J \right)\]

Bài 5: Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch gồm biến trở R mắc nối tiếp với tụ điện có điện dung C. Gọi điện áp hiệu dụng giữa hai đầu tu điện, giữa hai đầu biến trở và hệ số công suất của đoạn mạch khi biến trở có giá trị R₁ lần lượt là U_C1, U_R1 và cosφ₁; khi biến trở có giá trị R₂ thì các giá trị tương ứng nói trên là U_C2, U_R2 và cosφ₂.

Biết ${{U}_{C1}}=2{{U}_{C2}},{{U}_{R2}}=2{{U}_{R1}}.$ Giá trị của cosφ₁ và cosφ₂ là:

A. $\cos {{\varphi }_{1}}=\frac{1}{\sqrt{3}};\cos {{\varphi }_{2}}=\frac{2}{\sqrt{5}}$.

B. $\cos {{\varphi }_{1}}=\frac{1}{\sqrt{5}};\cos {{\varphi }_{2}}=\frac{1}{\sqrt{3}}$.

C. $\cos {{\varphi }_{1}}=\frac{1}{\sqrt{5}};\cos {{\varphi }_{2}}=\frac{2}{\sqrt{5}}$.

D. $\cos {{\varphi }_{1}}=\frac{1}{2\sqrt{2}};\cos {{\varphi }_{2}}=\frac{1}{\sqrt{2}}$.

Lời giải

Đáp án đúng: C

Ta có: ${{U}^{2}}=U_{R1}^{2}+U_{C1}^{2}=U_{R2}^{2}+U_{C2}^{2}$

$\Rightarrow U_{R1}^{2}+U_{C1}^{2}=4U_{R1}^{2}+\frac{U_{C1}^{2}}{4}\Leftrightarrow {{U}_{C1}}=2{{U}_{R1}}$

Khi đó: $U=\sqrt{U_{R1}^{2}+U_{C1}^{2}}=\sqrt{5}{{U}_{R1}}$

$\begin{array}{l}\cos {\phi }_1=\frac{U_{R1}}{U}=\frac{U_{R1}}{\sqrt{5}{U}_{R1}}=\frac{1}{\sqrt{5}}\\ \cos {\phi }_2=\frac{U_{R2}}{U}=\frac{2U_{R1}}{\sqrt{5}{U}_{R1}}=\frac{2}{\sqrt{5}}\end{array}$

Bài 6: Đầu O của một sợi dây đàn hồi nằm ngang dao động điều hoà với biên độ 3 cm với tần số 2 Hz. Sau 2 s sóng truyền được 2 m. Chọn gốc thời gian lúc đầu O đi qua vị trí cân bằng theo chiều dương. Li độ của điểm M trên dây cách O đoạn 2,5 m tại thời điểm 2 s là:

A. x_M = -3 cm. 

B. x_M = 0. 

C. x_M = 1,5 cm.       

D. x_M = 3 cm. 

Lời giải

Đáp án đúng: B

$v=\frac{s}{t}=\frac{2}{2}=1\left( \text{m/s} \right)\Rightarrow \lambda =\frac{v}{f}=\frac{1}{2}=0,5m$

Ta có:

${{u}_{O}}=3\cos \left( 4\pi t-\frac{\pi }{2} \right)cm\Rightarrow {{u}_{M}}=3\cos \left( 4\pi t-\frac{\pi }{2}-\frac{2\pi .2,5}{0,5} \right)=3\cos \left( 4\pi t-\frac{\pi }{2} \right)$

Tại $t=2\left( s \right)\Rightarrow {{u}_{M}}=0$

Bài 7: Một sóng cơ học được truyền theo phương Ox với vận tốc v =20 cm/s. Giả sử khi sóng truyền đi biên độ không thay đổi. Tại O sóng có phương trình: $x=4\cos \left( 4\pi t-\frac{\pi }{2} \right)$ , t đo bằng s. Tại thời điểm t₁ li độ tại điểm O là u =$\sqrt{3}$mm và đang giảm. Lúc đó ở điểm M cách O một đoạn 40 cm sẽ có li độ là:

A. 4 mm và đang tăng.

B. $\sqrt{3}$mm và đang tăng.

C. 3 mm và đang giảm.

D. $\sqrt{3}$mm và đang giảm.

Lời giải

Đáp án đúng: D

$\lambda =\frac{v}{f}=10\left( cm \right)$

Suy ra: $\Delta {{\varphi }_{MO}}=\frac{2\pi .40}{10}=8\pi $

Suy ra M cùng pha với O.

Nên tại thời điểm đó, M có li độ $\sqrt{3}$ mm và đang giảm.

Bài 8: Một electron bay với vận tốc 1,2.10⁷ m/s từ một điểm có điện thế V₁ = 600 V, theo hướng của các đường sức. Biết điện tích của electron là -1,6.10^-19 C và khối lượng của nó là 9,1.10^-31 kg. Điện thế V₂ của điểm mà ở đó electron dừng lại là

A. 150,4 V.                             

B. 170,5.                              

C. 190,5                    

D. 200 V.

Lời giải

Đáp án đúng: C

Áp dụng định lí động năng ta có: ${{W}_{d2}}-{{\text{W}}_{d1}}=A\Leftrightarrow -\frac{m{{v}^{2}}}{2}={{q}_{e}}\left( {{V}_{1}}-{{V}_{2}} \right)$

Suy ra: ${{V}_{2}}={{V}_{1}}+\frac{m{{v}^{2}}}{2{{q}_{e}}}=600+\frac{9,{{1.10}^{-31}}.{{\left( 1,{{2.10}^{-7}} \right)}^{2}}}{2.\left( -1,{{6.10}^{-19}} \right)}=190,5\left( V \right)$

Bài 9: Một con lắc đơn gồm vật nhỏ treo vào sợi dây không giãn có chiều dài đủ lớn. Tại một nơi trên mặt đất, con lắc dao động điều hòa với chu kì T. Giảm chiều dài dây treo con lắc đi 44 cm thì chu kì dao động của con lắc giảm đi 0,4 s. Lấy g = π² = 10 m/s². Giá trị của T bằng  

A. 0,4 s.

B. 2,4 s.

C. 2 s.

D. 1,2 s.

Lời giải

Đáp án đúng: B

Chu kì của con lắc đơn lúc đầu có chiều dài l là ${{T}^{2}}=4{{\pi }^{2}}\frac{\ell }{g}$ (1)

Theo đề bài: Giảm chiều dài dây treo con lắc đi 44 cm thì chu kì dao động của con lắc giảm đi 0,4 s.

$\Rightarrow {{\left( T-0,4 \right)}^{2}}=4{{\pi }^{2}}.\frac{\ell -0,44}{g}$ (2)

Lấy (1) - (2), ta được: \[{{T}^{2}}-{{\left( T-0,4 \right)}^{2}}=\frac{4{{\pi }^{2}}}{g}.\left( \ell -\ell +0,44 \right)\]

$\Rightarrow 0,4\left( 2T-0,4 \right)=\frac{4.10}{10}.0,44$

$\Rightarrow T=2,4s$

Bài 10: Một ô tô đang chuyển động với vận tốc không đổi 30 m/s. Đến chân một con dốc, đột nhiên máy ngừng hoạt động và ôtô theo đà đi lên dốc. Nó luôn luôn chịu một gia tốc ngược chiều với vận tốc đầu bằng 2 m/s² trong suốt quá trình lên dốc và xuống dốc. Chọn gốc toạ độ và gốc thời gian là nơi và lúc xe ở chân dốc. Quãng đường xa nhất theo sườn dốc mà ô tô có thể lên được là

A. 150 m.

B. 225 m.

C. 250 m.

D. 275 m.

Lời giải

Đáp án đúng: B

Từ lúc lên dốc đến khi dừng lại tại một vị trí trên sườn dốc, ô tô chỉ chuyển động theo một chiều trùng chiều dương của trục Ox nên:

Quãng đường xa nhất theo sườn dốc mà ô tô có thể lên được là:

$s=\frac{{{v}^{2}}-v_{0}^{2}}{2a}=\frac{0-{{30}^{2}}}{2.\left( -2 \right)}=225\left( m \right)$

Bài 11: Cuộn sơ cấp và thứ cấp của một máy biến áp có số vòng lần lượt là 600 vòng và 120 vòng. Đặt vào 2 đầu cuộn sơ cấp một điện áp xoay chiều có giá trị hiệu dụng 380V.

a. Tính điện áp giữa 2 đầu cuộn thứ cấp.

b. Nối 2 đầu cuộn thứ cấp với điện trở có R = 100Ω. Tính cường độ dòng điện chạy trong cuộn sơ cấp (bỏ qua mọi hao phí ở máy biến áp).

Lời giải

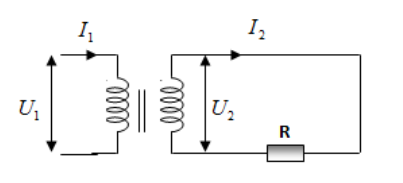
a. Vì bỏ qua hao phí ở máy biến áp, ta có: ${{U}_{2}}={{U}_{1}}\frac{{{N}_{2}}}{{{N}_{1}}}=380.\frac{120}{600}=76\left( V \right)$

b.

- Cường độ dòng điện chạy trong cuộn thứ cấp: 

${{I}_{2}}=\frac{{{U}_{2}}}{R}=\frac{76}{100}=0,76\left( A \right)$

- Cường độ dòng điện chạy trong cuộn sơ cấp:

${{I}_{1}}=\frac{{{N}_{2}}{{I}_{2}}}{{{N}_{1}}}=\frac{120.0,76}{600}=0,152\left( A \right)$

Bài 12: Một con lắc đơn dao động điều hoà tại địa điểm A với chu kì 2 s. Đưa con lắc này tới địa điểm B cho nó dao động điều hoà, trong khoảng thời gian 201s nó thực hiện được 100 dao động toàn phần. Coi chiều dài dây treo của con lắc đơn không đổi. Gia tốc trọng trường tại B so với tại A.

A. tăng 0,1%. 

B. tăng 1%.  

C. giảm 1%.    

D. giảm 0,1%.

Lời giải

Đáp án đúng: C

Chu kì dao động tại A: ${{T}_{A}}=2\pi \sqrt{\frac{\ell }{{{g}_{A}}}}=2\left( s \right)$

Chu kì dao động tại B: ${{T}_{B}}=2\pi \sqrt{\frac{\ell }{{{g}_{B}}}}=2,01\left( s \right)$

$\Rightarrow \frac{{{g}_{A}}}{{{g}_{B}}}=\frac{2,{{01}^{2}}}{{{2}^{2}}}\Rightarrow {{g}_{B}}=0,99{{g}_{A}}$

Vậy g_B­ giảm 1% so với g_A

Bài 13: Một lò xo treo thẳng đứng, đầu trên cố định, đầu dưới có gắn vật m = 100 g, độ cứng 25 N/m, lấy g = 10m/s². Chọn trục Ox thẳng đứng, chiều dương hướng xuống. Vật dao động với phương trình: \[x=4cos\left( 5\pi t+\frac{\pi }{3} \right)\] cm. Thời điểm lúc vật qua vị trí lò xo bị dãn 2cm lần đầu tiên là

A. $\frac{1}{5}s$.

B. $\frac{1}{25}s$.   

C. $\frac{1}{15}s$.  

D. $\frac{1}{30}s$.

Lời giải

Đáp án đúng: C

Độ dãn của lò xo tại VTCB: $\Delta l=\frac{mg}{k}=0,04\left( m \right)=4cm$

Thời điểm t = 0 và thời điểm vật qua vị trí lò xo bị dãn 2 cm lần đầu tiên được biểu diễn trên VTLG:

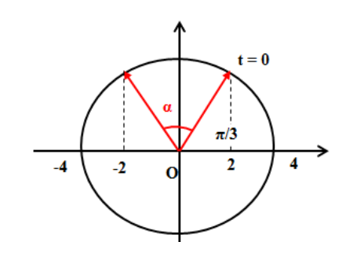
Góc quét được: $\alpha =\frac{\pi }{6}+\frac{\pi }{6}=\frac{\pi }{3}$

Vậy thời điểm lúc vật qua vị trí lò xo bị dãn 2 cm lần đầu tiên là:

$t=\frac{\alpha }{\omega }=\frac{\frac{\pi }{3}}{5\pi }=\frac{1}{15}s$

Bài 14: Chọn câu đúng về pha của li độ, vận tốc và gia tốc của dao động cơ điều hòa

A. vận tốc chậm pha $\frac{\pi }{2}$ so với li độ.

B. vận tốc ngược pha so với gia tốc.

C. li độ chậm pha $\frac{\pi }{2}$ so với vận tốc.

D. li độ cùng pha với gia tốc.

Lời giải

Đáp án đúng: C

Trong dao động điều hòa, a sớm pha hơn v góc $\frac{\pi }{2}$, v sớm pha hơn x góc $\frac{\pi }{2}$, a và x ngược pha.

Bài 15: Một mũi nhọn S chạm nhẹ vào mặt nước dao động điều hòa với tần số f = 40 Hz. Người ta thấy rằng hai điểm A và B trên mặt nước cùng nằm trên phương truyền sóng cách nhau một khoảng d = 20 cm luôn dao động ngược pha nhau. Biết vận tốc truyền sóng nằm trong khoảng từ 3 m/s đến 5 m/s. Vận tốc đó là

A. 5 m/s.  

B. 3,5 m/s. 

C. 3,2 m/s.  

D. 4,2 m/s.

Lời giải

Đáp án đúng: C

A và B cách nhau khoảng d = 20 cm luôn dao động ngược pha

$\Rightarrow \varphi =\frac{2\pi d}{\lambda }=\left( 2k+1 \right)\pi \Rightarrow \lambda =\frac{2d}{\left( 2k+1 \right)}\left( k\in Z \right)$

Vận tốc truyền sóng được xác định theo công thức:

$v=\lambda .f=\frac{2d.f}{2k+1}=\frac{2.0,2.40}{2k+1}=\frac{16}{2k+1}\left( k\in Z \right)$

Mà $3\le v\le 5\Rightarrow 3\le \frac{16}{2k+1}\le 5\Rightarrow 1,1\le k\le 2,16\Rightarrow k=2$

Thay vào v ta được: v = 3,2 m/s.

Bài 16: Một con lắc lò xo gồm quả cầu nhỏ khối lượng 500 g và lò xo có độ cứng 50 N/m. Cho con lắc dao động điều hòa trên phương nằm ngang. Tại thời điểm vận tốc của quả cầu là 0,1 m/s thì gia tốc của nó là $\sqrt{3}$m/s². Cơ năng của con lắc là

A. 0,04 J.

B. 0,05 J.

C. 0,02 J.

D. 0,01 J.

Lời giải

Đáp án đúng: D

Tần số góc: $\omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{50}{0,5}}=10\left( \text{rad/s} \right)$

Mà ${{\left( \frac{v}{\omega .A} \right)}^{2}}+{{\left( \frac{a}{{{\omega }^{2}}.A} \right)}^{2}}=1\Rightarrow A=0,02m$

Cơ năng của con lắc:

$W=\frac{1}{2}k{{A}^{2}}=\frac{1}{2}.50.0,{{02}^{2}}=0,01\left( J \right)$

Bài 17: Đặt vào hai đầu một cuộn dây thuần cảm (cảm thuần) có độ tự cảm L một hiệu điện thế u = U₀cosωt. Cường độ dòng điện chạy qua cuộn dây có biểu thức là 

A. $i={{U}_{0}}\omega L\cos \left( \omega t+\frac{\pi }{2} \right)$.

B. $i=\frac{{{U}_{0}}}{\omega L}\cos \left( \omega t-\frac{\pi }{2} \right)$.

C. $i=\frac{{{U}_{0}}}{\omega L}\cos \left( \omega t+\frac{\pi }{2} \right)$.

D. $i=\frac{{{U}_{0}}}{\omega L}\cos \left( \omega t \right)$.

Lời giải

Đáp án đúng: B

Đối với mạch chỉ chứa cuộn dây thuần cảm thì:

${{\varphi }_{{{u}_{L}}}}-{{\varphi }_{i}}=\frac{\pi }{2}\Rightarrow 0-{{\varphi }_{i}}=\frac{\pi }{2}\Rightarrow {{\varphi }_{i}}=-\frac{\pi }{2}$

Ta có: ${{I}_{0}}=\frac{{{U}_{0}}}{{{Z}_{L}}}=\frac{{{U}_{0}}}{L\omega }$

Vậy phương trình của i là:

$i=\frac{{{U}_{0}}}{\omega L}\cos \left( \omega t-\frac{\pi }{2} \right)$

Bài 18: Chọn câu sai? Dao động duy trì

A. có biên độ không đổi.

B. có chu kì không đổi.

C. có tần số bằng tần số riêng.

D. có biên độ phụ thuộc vào tần số của dao động.

Lời giải

Đáp án đúng: D

Dao động duy trì có biên độ không đổi và tần số dao động bằng tần số riêng của hệ.

Bài 19: Một vật thực hiện đồng thời 4 dao động điều hòa cùng phương, cùng tần số có các phương trình: x₁ = 3sin(πt + π) cm; x₂ = 3cos(πt) cm; x₃ = 2sin(πt + π) cm; x₄ = 2cos(πt) cm. Hãy xác định phương trình dao động tổng hợp của vật:

A. x = $\sqrt{5}$cos(πt + $\frac{\pi }{2}$) cm.     

B. x = $5\sqrt{2}$cos(πt + $\frac{\pi }{4}$) cm.

C. x = 5cos(πt + $\frac{\pi }{2}$) cm.

D. x = 5cos(πt - $\frac{\pi }{4}$) cm.

Lời giải

Đáp án đúng: B

Ta có: 

$x_1 =3sin\left(\pi t+\pi \right)=3\cos \left(\pi t+\frac{\pi }{2}\right)$;

$x_3 =2sin\left(\pi t+\pi \right)=2cos\left(\pi t+\frac{\pi }{2}\right)$;

Bấm máy tính ta được:

$x={{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}=3\angle \frac{\pi }{2}+3\angle 0+2\angle \frac{\pi }{2}+2\angle 0=5\sqrt{2}\angle \frac{\pi }{4}$

Vậy phương trình dao động tổng hợp:

\[x=5\sqrt{2}cos\left( \pi t+\frac{\pi }{4} \right)\]

Bài 20: Cho hai dao động điều hòa cùng phương, cùng tần số, cùng biên độ 2 cm và có các pha ban đầu là $\frac{\pi }{3}$ và $-\frac{\pi }{3}$. Pha ban đầu và biên độ của dao động tổng hợp của hai dao động trên là

A. 0 rad; 2 cm.

B. $\frac{\pi }{6}$ rad; 2 cm.

C. 0 rad; $2\sqrt{3}$ cm.

D. 0 rad; $2\sqrt{2}$ cm.

Lời giải

Đáp án đúng: A

Có: ${{A}^{2}}=A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos \Delta \varphi \Rightarrow A=2$

$\tan \varphi =\frac{{{A}_{1}}\sin {{\varphi }_{1}}+{{A}_{2}}\sin {{\varphi }_{2}}}{{{A}_{1}}co\operatorname{s}{{\varphi }_{1}}+{{A}_{2}}\cos {{\varphi }_{2}}}=0\Rightarrow \varphi =0$

Bài 21: Hai điện tích q₁ = q₂ = q > 0 đặt tại A và B trong không khí. Cho biết AB = 2a.

a. Xác định cường độ điện trường E_M tại điểm M trên đường trung trực của AB, cách AB một đoạn bằng h.

b. Xác định h để E_M cực đại. Tính giá trị cực đại này.

Lời giải

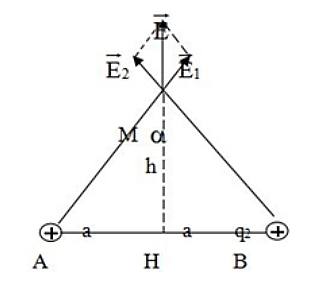
a. Cường độ điện trường tại M: ${{\vec{E}}_{M}}={{\vec{E}}_{1}}+{{\vec{E}}_{2}}$

${{E}_{1}}={{E}_{2}}=k\frac{q}{{{a}^{2}}+{{x}^{2}}}$

Từ hình vẽ, ta có:

$E=2{{E}_{1}}\cos \alpha =\frac{2kqh}{{{\left( {{a}^{2}}+{{h}^{2}} \right)}^{\frac{3}{2}}}}$

b. Để ${{E}_{M}}$đạt cực đại, áp dụng cô – si cho 3 số không âm:

${{a}^{2}}+{{h}^{2}}=\frac{{{a}^{2}}}{2}+\frac{{{a}^{2}}}{2}+{{h}^{2}}\ge 3\sqrt[3]{\frac{{{a}^{4}}{{h}^{2}}}{4}}$

\[\Rightarrow {{\left( {{a}^{2}}+{{h}^{2}} \right)}^{3}}\ge \frac{27}{4}{{a}^{4}}{{h}^{2}}\Rightarrow {{\left( {{a}^{2}}+{{h}^{2}} \right)}^{\frac{3}{2}}}\ge \frac{3\sqrt{3}}{2}{{a}^{2}}h\]

Do đó: ${{E}_{M}}\le \frac{2kqh}{\frac{3\sqrt{3}}{2}{{a}^{2}}h}=\frac{4kq}{3\sqrt{3}{{a}^{2}}}$

${{E}_{M}}$đạt cực đại khi: ${{h}^{2}}=\frac{{{a}^{2}}}{2}\Rightarrow h=\frac{a}{\sqrt{2}}\Rightarrow {{\left( {{E}_{M}} \right)}_{max}}=\frac{4kq}{3\sqrt{3}{{a}^{2}}}$

Bài 22: Một con lắc lò xo gồm lò xo nhẹ có độ cứng 20 N/m và vật nhỏ có khối lượng m. Con lắc dao động điều hoà với tần số 1,59 Hz. Giá trị của m là

A. 50 g.

B. 100 g.

C. 200 g.

D. 75 g.

Lời giải

Đáp án đúng: C

Ta có: $m=\frac{k}{{{\omega }^{2}}}=\frac{k}{{{\left( 2\pi f \right)}^{2}}}=0,2\left( kg \right)=200g$

Bài 23: Một con lắc đơn có dây treo dài 1m và vật có khối lượng m = 1kg dao động với biên độ góc 0,05rad. Chọn gốc thế năng tại vị trí cân bằng của vật, lấy g = 10 m/s². Cơ năng của con lắc là

A. 0,125 J.

B. 0,012 J.

C. 0,0125 J.

D. 0,025 J.

Lời giải

Đáp án đúng: C

Cơ năng của con lắc là

$W=\frac{1}{2}mgl\alpha _{0}^{2}=\frac{1}{2}.1.10.1.0,{{05}^{2}}=0,0125J$

Bài 24: Trên mặt nước có hai nguồn kết hợp S₁, S₂ cách nhau $6\sqrt{2}$ cm dao động theo phương trình u = acos20πt(mm). Tốc độ truyền sóng trên mặt nước là 0,4 m/s và biên độ sóng không đổi trong quá trình truyền. Điểm gần nhất ngược pha với các nguồn nằm trên đường trung trực của S₁S₂ cách S₁S₂ một đoạn:

A. 6 cm.    

B. 2 cm.   

C. $3\sqrt{2}$cm.

D. 18 cm.

Lời giải

Đáp án đúng: C

Ta có: $\lambda =\frac{v}{f}=4\left( cm \right)$

Phương trình sóng tại điểm M trên đường trung trực là:

${{u}_{M}}=2a\cos \left( \frac{\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda } \right)\cos \left( 2\pi t-\frac{\pi \left( {{d}_{1}}+{{d}_{2}} \right)}{\lambda } \right)=2a\cos \left( 2\pi t-\frac{2\pi d}{\lambda } \right)\left( {{d}_{1}}={{d}_{2}}=d \right)$

Để M dao động ngược pha với nguồn thì

$\frac{2\pi d}{\lambda }=\left( 2k+1 \right)\pi \Rightarrow d=\left( k+0,5 \right)\lambda =4\left( k+0,5 \right)$

Mặt khác: $d>\frac{AB}{2}\Rightarrow 4\left( k+0,5 \right)>3\sqrt{2}\Leftrightarrow k>0,56$

$\Rightarrow k=1\Rightarrow {{d}_{\min }}=6$

Khoảng cách từ M đến S₁S₂: $d\left( M;{{S}_{1}}{{S}_{2}} \right)=\sqrt{{{6}^{2}}-{{\left( 3\sqrt{2} \right)}^{2}}}=3\sqrt{2}$

Bài 25: Một vật sáng AB đặt cách màn chắn một khoảng L = 90 cm. Trong khoảng giữa vật sáng và màn chắn đặt một thấu kính hội tụ có tiêu cự f sao cho trục chính của thấu kính vuông góc với vật AB và màn. Khoảng cách giữa hai vị trí đặt thấu kính để cho ảnh rõ nét trên màn chắn là l = 30 cm. Tính tiêu cự của thấu kính hội tụ.

A. 10 cm.

B. 20 cm.

C. 30 cm.

D. 40 cm.

Lời giải

Đáp án đúng: B

Theo đề ta có:

$\ell ={{d}_{1}}-{{d}_{2}}=\frac{L+\sqrt{{{L}^{2}}-4Lf}}{2}-\frac{L-\sqrt{{{L}^{2}}-4Lf}}{2}=\sqrt{{{L}^{2}}-4Lf}$

$\Rightarrow \ell ={{L}^{2}}-4Lf\Rightarrow f=20\left( cm \right)$

Bài 26: Một vật dao động điều hoà với chu kỳ T = 1,2 s và vận tốc cực đại khi vật qua vị trí cân bằng là 4π cm/s. Biên độ dao động của vật là

A. 2,4 cm.

B. 3,3 cm.

C. 6 cm.

D. 5,5 cm.

Lời giải

Đáp án đúng: A

Ta có, vận tốc cực đại: ${{v}_{max}}=A\omega =\frac{2\pi A}{T}\Rightarrow A=\frac{T.{{v}_{max}}}{2\pi }=2,4\left( cm \right)$

Bài 27: Một con lắc lò xo gồm một vật nặng có khối lượng 500 g treo vào đầu lò xo có độ cứng k = 2,5 N/cm. Kích thích cho vật dao động, vật có gia tốc cực đại 5 m/s². Biên độ dao động của vật là

A.$\sqrt{5}$cm.                        

B. 2 cm.                        

C. 5 cm.                          

D. 1 cm.

Lời giải

Đáp án đúng: D

Độ cứng: $k=250N/m$

Tần số góc: $\omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{250}{0,5}}=10\sqrt{5}$rad/s

Gia tốc cực đại: ${{a}_{max}}={{\omega }^{2}}A\Rightarrow A=\frac{{{a}_{max}}}{{{\omega }^{2}}}=\frac{5}{{{\left( 10\sqrt{5} \right)}^{2}}}=1\left( cm \right)$

Bài 28: Một con lắc đơn dao động điều hoà, nếu tăng chiều dài 25% thì chu kỳ dao động của nó

A. tăng 25%.

B. giảm 25%.

C. tăng 11,80%.

D. giảm 11,80%.

Lời giải

Đáp án đúng: C

$\frac{{{T}'}}{T}=\frac{2\pi \sqrt{\frac{{{\ell }'}}{g}}}{2\pi \sqrt{\frac{\ell }{g}}}=\sqrt{\frac{{{\ell }'}}{\ell }}=\sqrt{\frac{1,25}{1}}\approx 1,118\Rightarrow {T}'=1,118T$

Chu kì dao động tăng: $\Delta T={T}'-T=0,118T$

Bài 29: Một vật dao động điều hoà, khi vật có li độ x₁ = 4 cm thì vận tốc $v_1=-40\sqrt{3}$ cm/s; khi vật có li độ $x_2=4\sqrt{2}$ cm thì vận tốc ${{v}_{2}}=40\sqrt{2}$cm/s; π² = 10. Động năng biến thiên với chu kỳ

A. $\frac{\pi }{10}s$.     

B. 0,8 s.      

C. 0,2 s.      

D. 0,4 s.

Lời giải

Đáp án đúng: A

Áp dụng công thức độc lập với thời gian ta được:

${{A}^{2}}=x_{1}^{2}+\frac{v_{1}^{2}}{{{\omega }^{2}}}=x_{2}^{2}+\frac{v_{2}^{2}}{{{\omega }^{2}}}\Rightarrow \omega =\sqrt{\frac{v_{1}^{2}-v_{2}^{2}}{x_{2}^{2}-x_{1}^{2}}}=10$rad/s

$\Rightarrow T=\frac{2\pi }{\omega }=\frac{\pi }{5}\left( s \right)$

Động năng dao động với chu kì:${T}'=\frac{T}{2}=\frac{\pi }{10}\left( s \right)$

Bài 30: Con lắc kép có chu kì T = 2 s với biên độ góc α₀ = 0,2 rad. Viết phương trình dao động của con lắc với gốc thời gian là lúc qua VTCB theo chiều dương.

A. α = 0,2cos(πt - $\frac{\pi }{2}$) rad.

B. α = 0,2cos(πt - $\frac{\pi }{6}$) rad.

C. α = 0,2cos(πt - $\frac{\pi }{5}$) rad.

D. α = 0,2cos(πt - $\frac{\pi }{8}$) rad.

Lời giải

Đáp án đúng: A

Tần số góc: ω = $\frac{2\pi }{T}$= π (rad/s)

Biên độ góc: α₀ = 0,2rad

Gốc thời gian là lúc vật qua VTCB theo chiều dương => φ = $-\frac{\pi }{2}$.

=> Phương trình dao động: α = 0,2cos(πt $-\frac{\pi }{2}$) rad.

Bài 31: Có hệ con lắc lò xo treo thẳng đứng và hệ con lắc đơn cùng dao động điều hòa tại một nơi nhất định. Chu kì dao động của chúng bằng nhau, nếu chiều dài của con lắc đơn:

A. Bằng độ biến dạng của lò xo khi vật ở vị trí thấp nhất.

B. Bằng chiều dài tự nhiên của lò xo.

C. Bằng độ biến dạng của lò xo khi vật ở vị trí cân bằng.

D. Bằng chiều dài của lò xo khi vật ở vị trí cân bằng.

Lời giải

Đáp án đúng: C

Chu kì dao động của con lắc đơn: $T=2\pi \sqrt{\frac{\ell }{g}}$

Chu kì dao động của con lắc lò xo: ${T}'=2\pi \sqrt{\frac{m}{k}}=2\pi \sqrt{\frac{\Delta {{\ell }_{0}}}{g}}$

Để chu kì của chúng bằng nhau $\Leftrightarrow T={T}'\Rightarrow 2\pi \sqrt{\frac{\ell }{g}}=2\pi \sqrt{\frac{\Delta {{\ell }_{0}}}{g}}\Rightarrow \Delta {{\ell }_{0}}=\ell $

Bài 32: Một vật dao động điều hòa trên trục Ox, khi vật đi từ điểm M có $x_1=\frac{A}{2}$ theo chiều âm đến điểm N có li độ $x_2=-\frac{A}{2}$ lần thứ nhất mất $\frac{1}{30}$s. Tần số dao động của vật là:

A. 5 Hz.

B. 10 Hz.

C. 5π Hz.

D. 10π Hz.

Lời giải

Đáp án đúng: A

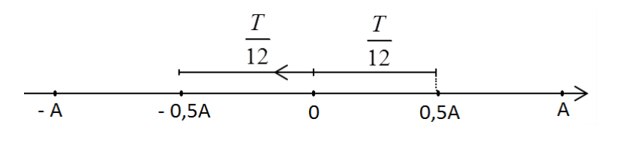
Ta có: $t=\frac{1}{30}=\frac{T}{12}+\frac{T}{12}\Rightarrow T=\frac{1}{5}\left( s \right)\Rightarrow f=5Hz$

Bài 33: Một con lắc lò xo đặt nằm ngang gồm lò xo có độ cùng k = 40 N/m và vật năng có khối lượng m = 400 g. Từ vị trí cân bằng kéo vật ra một đoạn 10 cm rồi thả nhẹ cho vật dao động. Trong quá trình dao động thì công suất tức thời cực đại của lực hồi phục là

A. 0,25 W.      

B. 2 W.  

C. 0,5 W.       

D. 1 W.

Lời giải

Đáp án đúng: B

Trong quá trình dao động thì công suất tức thời cực đại của lực hồi phục là

$\begin{array}{l}P=F_{hp}.v=-kx.v\\ =-\frac{k{A}^2{\omega }^2}{2}\sin 2\left(\omega t+\phi \right)\end{array}$

$\Rightarrow {{P}_{max}}=\frac{k{{A}^{2}}\omega }{2}=\frac{40.0,{{1}^{2}}.\sqrt{\frac{40}{0,4}}}{2}=2\left( \text{W} \right)$

Bài 34: Một vật nhỏ có khối lượng m = 100 g đồng thời thực hiện hai dao động điều hòa cùng phương, cùng tần số. Ở thời điểm t bất kì, li độ của hai dao động thành phần luôn thỏa mãn $16x_{1}^{2}+9x_{2}^{2}=36$ (x₁, x₂ tính bằng cm). Biết lực hồi phục cực đại tác dụng lên chất điểm trong quá trình dao động là F = 0,25 N; lấy π² = 10. Tốc độ cực đại của vật trong quá trình dao động là

A. 40 cm/s.                        

B. 25 m/s.                          

C. 25 cm/s.                        

D. 40 m/s.

Lời giải

Đáp án đúng: C

Theo bài ra ta có: $16x_{1}^{2}+9x_{2}^{2}=36\Leftrightarrow \frac{x_{1}^{2}}{1,{{5}^{2}}}+\frac{x_{2}^{2}}{{{2}^{2}}}=1$

⇒ dao động x₁ vuông pha x₂

$\Rightarrow {{A}_{1}}=1,5\left( cm \right);{{A}_{2}}=2\left( cm \right)$

Biên độ dao động tổng hợp: $A=\sqrt{A_{1}^{2}+A_{2}^{2}}=2,5\left( cm \right)$

Mặt khác: \[{{F}_{max}}=m{{\omega }^{2}}A=\frac{m{{\omega }^{2}}{{A}^{2}}}{A}=\frac{mv_{max}^{2}}{A}\]

$\Rightarrow {{v}_{max}}=\sqrt{\frac{A.{{F}_{max}}}{m}}=\sqrt{\frac{0,025.0,25}{0,1}}=0,25$ m/s

Bài 35: Mạch RLC mắc nối tiếp. Biết R= 100Ω, L = $\frac{1}{\pi }$ (H) và C thay đổi được. Hiệu điện thế hai đầu mạch có biểu thức u = $200\sqrt{2}$cos100πt (V). Thay đổi C để hệ số công suất mạch đạt cực đại. Khi đó cường độ hiệu dụng trong mạch bằng:

A. 1 A.

B. $\sqrt{2}$A.

C. 2 A.

D. $2\sqrt{2}$ A.

Lời giải

Đáp án đúng: C

Ta có Z_L = 100 $\Omega $, R = 100 $\Omega $

=> Hệ số công suất cos $\varphi $ = $\frac{R}{Z}=\frac{R}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}$

Khi đó để C thay đổi để cos${{\varphi }_{max}}$ thì Z_L = Z_C = 100 $\Omega $ 

=> Cường độ dòng điện hiệu dụng trong mạch là:

I = $\frac{U}{Z}$ = $\frac{U}{R}$ = $\frac{200}{100}$ = 2 A

Bài 36: Cho 3 quả cầu kim loại tích điện lần lượt tích điện là +3C, -7C và –4C. Khi cho chúng được tiếp xúc với nhau thì điện tích của hệ là

A. – 8 C.

B. + 14 C.

C. + 3 C.

D. – 11 C.

Lời giải

Đáp án đúng: A

Khi cho 3 điện tích tiếp xúc với nhau thì tổng điện tích của hệ không đổi:

$q={{q}_{1}}+{{q}_{2}}+{{q}_{3}}=-8C$

Bài 37: Cường độ dòng điện tức thời chạy qua một đoạn mạch điện xoay chiều là i = 4cos(20 πt - $\frac{\pi }{2}$)(A), t đo bằng giây. Tại thời điểm t₁ (s) nào đó dòng điện đang giảm và có cường độ bằng i₁ = - 2A. Hỏi đến thời điểm t₂ = (t₁ + 0,025)(s) cường độ dòng điện bằng bao nhiêu?

A. \(2\sqrt 3 \,A\).

B. \( - 2\sqrt 3 \,A\).

C. \( - \sqrt 3 \,A\).

D. – 2 A.

Lời giải

Đáp án đúng: B

Chu kì T = \(\frac{{2\pi }}{\omega } = \frac{{2\pi }}{{20\pi }} = \frac{1}{{10}}\,s\)

Tại thời điểm t₁ (s) nào đó dòng điện đang giảm và có cường độ bằng i₁ = - 2A.

⇒ Vecto cường độ dòng điện đang đi về biên âm.

⇒ Kể từ vị trí ban đầu vecto cường độ dòng điện đang ở vị trí cân bằng theo chiều dương thì thời gian để vecto cường độ dòng điện tới vị trí i₁ là:

t₁ = \(\frac{T}{2} + \frac{T}{{12}} = \frac{7}{{12}}T\) = \(\frac{7}{{120}}\,s\)

\( \Rightarrow {t_2} = \frac{7}{{120}} + 0,025 = \frac{1}{{12}}\,\,s\)

=> i = 4cos(20πt₂ – \(\frac{\pi }{2}\)) = 4cos(20π.\(\frac{1}{{12}}\)– \(\frac{\pi }{2}\)) =\( - 2\sqrt 3 \,A.\)

Bài 38: Sóng ngang truyền trên sợi dây đàn hồi với bước sóng λ. Trên dây có hai điểm P, Q cách nhau $\frac{\lambda }{2}$, khi P có li độ cực đại thì Q có

A. li độ cực đại.

B. tốc độ cực đại.

C. thế năng cực tiểu.

D. li độ cực tiểu.

Lời giải

Đáp án đúng: D

Sóng ngang truyền trên sợi dây đàn hồi với bước sóng λ. Trên dây có hai điểm P, Q cách nhau \(\frac{\lambda }{2}\), khi P có li độ cực đại thì Q có li độ cực tiểu.

Bài 39: Đoạn mạch xoay chiều RLC mắc nối tiếp. Điện trở thuần R = 100$\Omega$, cuộn dây thuần cảm có độ tự cảm L, tụ có điện dung $C=\frac{{10}^{-4}}{\pi }F.$ Mắc vào hai đầu đoạn mạch điện áp xoay chiều u = U sin(100πt) V. Để điện áp hai đầu đoạn mạch cùng pha với điện áp hai đầu điện trở R thì giá trị độ từ cảm của cuộn dây là

A. \(L = \frac{1}{\pi }\left( H \right)\).

B. \(L = \frac{{10}}{\pi }\left( H \right)\).

C. \(L = \frac{1}{{2\pi }}\left( H \right)\).

D. \(L = \frac{2}{\pi }\left( H \right)\).

Lời giải

Đáp án đúng: A

Điện áp hai đầu đoạn mạch cùng pha với điện áp hai đầu điện trở R.

⇒ Điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện.

Khi đó:

$\begin{array}{l}\tan \phi =\frac{Z_L-Z_C}{R}\\ \Rightarrow \tan 0^0=\frac{Z_L-Z_C}{R}\Rightarrow Z_L=Z_C\end{array}$

Ta có: 

$\begin{array}{l}{Z}_L=Z_C\Rightarrow L\omega =\frac{1}{C\omega }\\ \Rightarrow L=\frac{1}{{\omega }^{2}C}\\ =\frac{1.\pi }{{\left(100\pi \right)}^2{.10}^{-4}}=\frac{1}{\pi }\left(H\right)\end{array}$

Bài 40: Hai điện tích điểm q₁ = 0,5 nC và q₂ = - 0,5 nC đặt tại hai điểm A, B cách nhau 6 cm trong không khí. Cường độ điện trường tại điểm M nằm trên trung trực của AB, cách trung điểm của AB một khoảng l = 4 cm có độ lớn là

A. E = 0 V/m.     

B. E = 1080 V/m.      

C. E = 1800 V/m.        

D. E = 2160 V/m.

Lời giải

Đáp án đúng: D

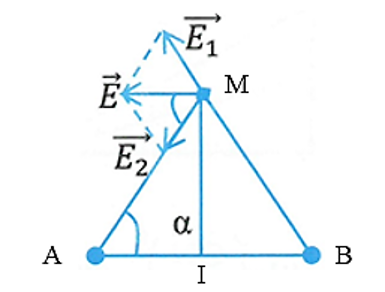
\(AI = BI = \frac{{AB}}{2} = 3\left( {cm} \right)\)

$AM=BM=\sqrt{3^2+4^2}=5\left(cm\right)$

\({E_A} = {E_B} = {9.10^9}.\frac{{0,{{5.10}^{ - 9}}}}{{0,{{05}^2}}} = 1800\left( {{\rm{V/m}}} \right)\)

\(\widehat {AMI} = {\rm{ar}}\cos \frac{4}{5} = 36,{86^0} \Rightarrow \widehat {AMB} = 73,{7^0}\)

\( \Rightarrow \left( {{{\vec E}_A},{{\vec E}_B}} \right) = {180^0} - 73,{7^0} = 106,{3^0} = \alpha \)

\({E_M} = 2{E_A}\cos \frac{\alpha }{2} = 2160\)V/m

Bài 41: Một con lắc dao động tắt dần. Cứ sau mỗi chu kì, biên độ giảm 3%. Phần năng lượng của con lắc bị mất đi trong một dao động toàn phần là bao nhiêu?

Lời giải

Ta có: \(\left\{ \begin{array}{l}{\rm{W}} = \frac{1}{2}k{A^2}\\{\rm{W'}} = \frac{1}{2}k{{A'}^2}\end{array} \right.\)

Sau 1 chu kì phần năng lượng của con lắc mất đi là:

\(\frac{{{\rm{W}} - {\rm{W'}}}}{{\rm{W}}} = \frac{{{A^2} - {{A'}^2}}}{{{A^2}}} = \frac{{{A^2} - {{\left( {1 - 0,03} \right)}^2}{A^2}}}{{{A^2}}} = 0,0591 = 5,91\% \)

Bài 42: Một vật đồng thời tham gia hai dao động điều hòa cùng phương, cùng tần số có các phương trình lần lượt là $x_1=3cos\left(10t+\frac{\pi }{3}\right)cm$, \(x = {A_2}cos\left( {10t - \frac{\pi }{6}} \right)\,cm\). Tốc độ của vật khi qua vị trí cân bằng là 50 cm/s. Biên độ dao động thành phần thứ hai là

A. 2 cm.

B. 1 cm.

C. 4 cm.

D. 5 cm.

Lời giải

Đáp án đúng: C

Ta có khi vật qua vị trí cân bằng thì

v_max = $A.\omega =50cm/s\Rightarrow A=\frac{50}{10}=5cm$

Mà 2 dao động vuông pha nhau nên $A=\sqrt{A_1^2+A_2^2}\iff A_2=\sqrt{5^2-3^2}=4cm$

Bài 43: Một con lắc đơn có l = 1 m; g = 10 m/s² được treo trên một xe ô tô, khi xe đi qua phần đường mấp mô, cứ 12 m lại có một chỗ ghềnh. Tính vận tốc của vật để con lắc dao động mạnh nhất?

A. 6 m/s.

B. 6 km/h.

C. 60 km/h.

D. 36 km/s.

Lời giải

Đáp án đúng: A

Chu kì dao động của con lắc đơn là: T = \(2\pi \sqrt {\frac{\ell }{g}} \)= 2 s.

Để con lắc dao động mạnh nhất thì chu kì của xe bằng chu kì riêng của con lắc đơn: \(v = \frac{S}{T} = \frac{{12}}{2} = 6\left( {{\rm{m/s}}} \right)\)

Bài 44: Vào cùng một thời điểm nào đó, hai dòng điện xoay chiều $i_1=I_{0}cos\left(\omega t+{\phi }_1\right)$ và $i_2=I_{0}cos\left(\omega t+{\phi }_2\right)$ đều có cùng giá trị tức thời là \(0,5{I_0}\)nhưng một dòng điện đang giảm, còn một dòng điện đang tăng. Hai dòng điện này lệch pha nhau một góc bằng:

A. \(\frac{{5\pi }}{6}\).   

B. \(\frac{{2\pi }}{3}\).   

C. \(\frac{\pi }{6}\).

D. \(\frac{{4\pi }}{3}\).

Lời giải

Đáp án đúng: B

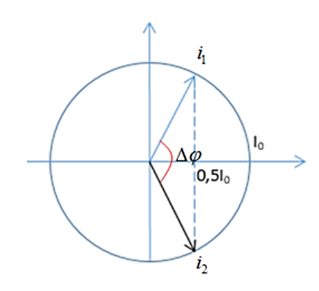
Từ vòng tròn lượng giác ta có, độ lệch pha giữa hai dòng điện này là: $\Delta \phi =\frac{2\pi }{3}$.

Bài 45: Trong dao động điều hòa thì gia tốc

A. cùng pha với vận tốc.

B. vuông pha với li độ.

C. cùng pha với lực kéo.

D. trễ pha \(\pi \) so với li độ.

Lời giải

Đáp án đúng: C

Trong dao động điều hòa thì gia tốc cùng pha với lực kéo \(\left( {F = ma} \right)\).

Bài 46: Hai dao động điều hòa cùng phương, cùng tần số có biên độ lần lượt là A₁ = 3cm, A₂ = 4cm và lệch pha nhau $\frac{\pi }{2}$. Dao động tổng hợp của hai dao động này có biên độ bằng:

A. \(3\sqrt 2 \)cm.

B. 3,2 cm.

C. 5 cm.

D. 7 cm.

Lời giải

Đáp án đúng: C

Biên độ dao động tổng hợp: $A=\sqrt{3^2+4^2+\mathrm{2.3.4.}\cos \frac{\pi }{2}}=5\left(cm\right)$

Bài 47: Hai điện tích q₁ = 5.10^-9 (C) , q₂ = -5.10^-9 (C) đặt tại hai điểm cách nhau 10 (cm) trong chân không. Độ lớn cường độ điện trường tại điểm nằm trên đường thẳng đi qua hai điện tích và cách q₁ 5 (cm), cách q₂ 15 (cm) là:

A. E = 16000 (V/m).             

B. E = 20000 (V/m).     

C.  E = 1,600 (V/m). 

D.  E = 2,000 (V/m).

Lời giải

Đáp án đúng: A

Áp dụng công thức tính cường độ điện trường tìm E₁ và E₂:

\(\begin{array}{l}{E_1} = k\frac{{\left| {{q_1}} \right|}}{{r_1^2}} = 18000\left( {{\rm{V/m}}} \right)\\{E_2} = k\frac{{\left| {{q_2}} \right|}}{{r_2^2}} = 2000\left( {{\rm{V/m}}} \right)\end{array}\)

Áp dụng nguyên lý chồng chất điện trường thấy ${\overrightarrow{E}}_1\uparrow \downarrow {\overrightarrow{E}}_2$:

\(\vec E = {\vec E_1} + {\vec E_2} \Rightarrow E = \left| {{E_1} - {E_2}} \right| = 16000\left( {{\rm{V/m}}} \right)\)

Bài 48: Một vật dao động điều hòa với phương trình x = 4cos(2πt – $\frac{\pi }{3}$) cm. Tốc độ trung bình cực tiểu mà vật đạt được trong khoảng thời gian \(\frac{2}{3}\) chu kỳ dao động là (lấy gần đúng)

A. 18,92 cm/s.                     

B. 18 cm/s.                     

C. 13,6 cm/s.                                  

D. 15,51 cm/s.

Lời giải

Đáp án đúng: C

+ Chu kì dao động: T = 1 s

+ Ta có: \(\Delta t = \frac{{2T}}{3} = \frac{T}{2} + \frac{T}{6} \Rightarrow {S_{\min }} = 2A + {s_{\min \frac{T}{6}}}\)

⇒ Góc quét được trong khoảng thời gian \(\frac{T}{6}\) là \(\frac{\pi }{3}\).

+ Quãng đường vật đi được trong \(\frac{1}{2}\) chu kì là 2A.

+ Vật có v = 0 khi qua vị trí biên => Trong cùng một khoảng thời gian vật đi được quãng đường nhỏ nhất khi đi xung quanh vị trí biên. Biểu diễn trên đường lượng giác, ta có:

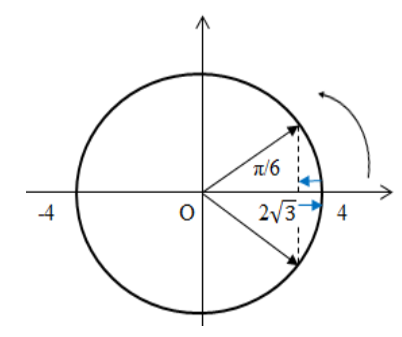
\( \Rightarrow {s_{\min \frac{T}{6}}} = 2\left( {4 - 2\sqrt 3 } \right) = 1,0718\left( {cm} \right) \Rightarrow {S_{\min }} = 9,0718\left( {cm} \right)\)

Tốc độ trung bình cực tiểu mà vật đạt được trong \(\frac{{2T}}{3}\):

\({v_{tb\min }} = \frac{{{S_{\min }}}}{{\Delta t}} = \frac{{9,0718}}{{\frac{2}{3}}} = 13,6\left( {{\rm{cm/s}}} \right)\)

Bài 49: Trên mặt nước có hai nguồn kết hợp A, B cách nhau 8 cm, dao động cùng pha với bước sóng phát ra là 1,5 cm. Một đường thẳng xx’ // AB và cách AB một khoảng 6 cm. M là điểm dao động với biên độ cực đại trên xx’ và gần A nhất. Hỏi M cách trung điểm của AB một khoảng bằng bao nhiêu?

A. 4,66 cm.   

B. 7,60 cm. 

C. 4,16 cm.    

D. 4,76 cm.

Lời giải

Đáp án đúng: B

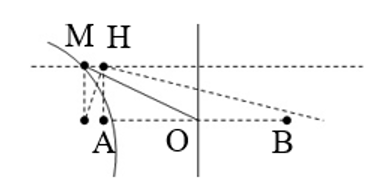
Giả sử H là cực đại: $AH-BH=k\lambda \Rightarrow k=-2,67$

Để cực đại nằm trên xx’ gần A nhất thì nó gần H nhất

Vì vậy, cực đại gần H nhất ứng với k = 3

Áp dụng tính chất đường Hypebol:

\(\frac{{x_M^2}}{{{a^2}}} - \frac{{y_M^2}}{{{b^2}}} = 1 \Rightarrow {x_M} = a\sqrt {1 + \frac{{y_M^2}}{{{b^2}}}} \)

Với:

\(\begin{array}{l}a = \frac{{\left| {{d_1} - {d_2}} \right|}}{2} = \frac{{\left| {k\lambda } \right|}}{2} = 2,25\\c = \frac{{AB}}{2} = 4\\{b^2} = {c^2} - {a^2} = 10,9375\end{array}\)

\( \Rightarrow {x_M} = 4,66\left( {cm} \right) \Rightarrow MO = 7,60\left( {cm} \right)\)

Bài 50: Hai dao động cùng phương, cùng biên độ A, cùng tần số và ngược pha nhau. Biên độ của dao động tổng hợp của hai dao động trên là

A. 0.             B. 2 A.         C. \(\frac{A}{2}\).           D. 4 A.

Lời giải

Đáp án đúng: A

Do 2 dao động ngược pha: \(A = \left| {{A_1} - {A_2}} \right| = 0\)

Bài 51: Một lăng kính có góc chiết quang A = 30°, chiết suất n = 1,5. Chiếu một tia sáng tới mặt lăng kính dưới góc tới i. Tính i để tia sáng ló ra khỏi lăng kính.

Lời giải

Để có tia sáng ló ra khỏi lăng kính thì \({i_1} \ge {i_0}\)

Với 

$\begin{array}{l}\sin i_0=n\sin \left(A-i_{gh}\right)\\ =1,5\sin \left(30-\text{ar}\sin \left(\frac{1}{1,5}\right)\right)\\ =-0,307\Rightarrow i_0=-17,{87}^0\end{array}$

$\Rightarrow i_1\ge -17,{87}^0$

Vậy để có tia ló ra khỏi lăng kính thì góc tới phải thỏa mãn: \( - 17,{87^0} \le {i_1} \le {90^0}\)

Bài 52: Cho một mạch điện xoay chiều AB gồm điện trở thuần R = 100 Ω, cuộn dây thuần cảm L, tụ điện có điện dung C. Đặt vào hai đầu đoạn mạch một hiệu điện thế xoay chiều không đổi u = 220\(\sqrt 2 \)cos(100 πt) (V), biết Z_L= 2Z_C. Ở thời điểm t hiệu điện thế hai đầu điện trở R là 60 V, hai đầu tụ điện là 40 V. Hỏi hiệu điện thế hai đầu đoạn mạch AB khi đó là:

A. \(220\sqrt 2 V\).

B. 72,11 V.

C. 100 V.

D. 20 V.

Lời giải

Đáp án đúng: D

Ta có: 

$\begin{array}{l}{Z}_L=2Z_C\\ \Rightarrow u_L=-2u_C\\ =-2.40=-80\left(V\right)\end{array}$

Hiệu điện thế hai đầu đoạn mạch AB ở thời điểm t là:

\(u = {u_R} + {u_L} + {u_C} = 60 + \left( { - 80} \right) + 40 = 20\left( V \right)\)

Bài 53: Một lò xo có độ cứng k = 16N/m có một đầu được giữ cố định còn đầu kia gắn vào quả cầu khối lượng M = 240 g đang đứng yên trên mặt phẳng nằm ngang. Một viên bi khối lượng m = 10 g bay với vận tốc v_­o­ = 10 m/s theo phương ngang đến gắn vào quả cầu và sau đó quả cầu cùng viên bi dao động điều hòa trên mặt phẳng nằm ngang. Bỏ qua ma sát và sức cản không khí. Biên độ dao động của hệ là

A. 5 cm.

B. 10 cm.

C. 12,5 cm.

D. 2,5 cm.

Lời giải

Đáp án đúng: B

Va cham mềm nên động lượng của hệ 2 vật (M và m) bảo toàn:

mv₀ = (m + M) V.

Suy ra vận tốc của hệ 2 vật ngay lúc va chạm:

\(v = \frac{{m{v_0}}}{{m + M}} = \frac{{0,01.10}}{{0,01 + 0,240}} = 0,4\)m/s

Hệ 2 vật dao động với tần số góc mới:

${\omega }^{\text{'}}=\sqrt{\frac{k}{m+M}}=\sqrt{\frac{16}{0,01+0,24}}=8$ rad/s

Vì hệ nằm ngang nên biên độ dao động được tính theo công thức:

$A=\sqrt{x^2+{\left(\frac{v}{\omega }\right)}^2}=10\left(cm\right)$

Bài 54: Một con lắc đơn chiều dài 20 cm dao động với biên độ góc 6⁰ tại nơi có g = 9,8m/s². Chọn gốc thời gian lúc vật đi qua vị trí có li độ góc 3⁰ theo chiều dương thì phương trình li độ góc của con lắc là:

A. $\alpha =\frac{\pi }{30}\sin \left(7t+\frac{\pi }{6}\right)\left(rad\right)$.

B. $\alpha =\frac{\pi }{30}\cos \left(7t-\frac{\pi }{3}\right)\left(rad\right)$.

C. $\alpha =\frac{\pi }{30}\cos \left(7t+\frac{\pi }{3}\right)\left(rad\right)$.

D. $\alpha =\frac{\pi }{30}\cos \left(7t-\frac{\pi }{6}\right)\left(rad\right)$.

Lời giải

Đáp án đúng: B

Biên độ góc: \({\alpha _0} = {6^0} = \frac{{6.\pi }}{{180}} = \frac{\pi }{{30}}\left( {rad} \right)\)

Tần số góc: $\omega =\sqrt{\frac{g}{\mathcal{l}}}=7$ rad/s

Chọn gốc thời gian là lúc vật qua vị trí có li độ 3⁰ theo chiều dương

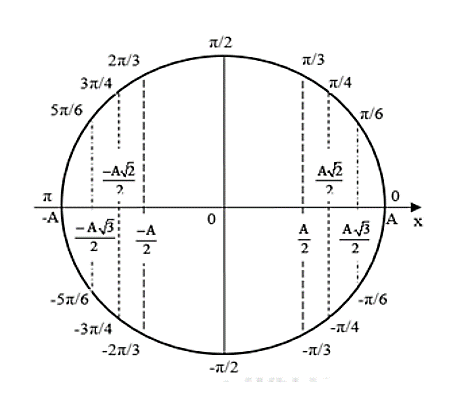
Sử dụng VTLG ta xác định được pha ban đầu: $\phi =\frac{-\pi }{3}$ rad

Vậy phương trình li độ góc của vật là: $\alpha =\frac{\pi }{30}\cos \left(7t-\frac{\pi }{3}\right)\left(rad\right)$

Bài 55: Một vật dao động điều hòa quanh VTCB O. Tại thời điểm t₁, vật có li độ x₁ và vận tốc v₁. Tại thời điểm t₂, vật có li độ \({x_2}\) và vận tốc \({v_2}.\) Mối liên hệ nào sau đây là đúng?

A. \(v_1^2 = v_2^2 + {\omega ^2}\left( {x_1^2 - x_2^2} \right)\).

B. \(x_1^2 = x_2^2 + {\omega ^2}\left( {v_1^2 - v_2^2} \right)\).

C. \(x_1^2 = x_2^2 + {\omega ^2}\left( {v_2^2 - v_1^2} \right)\).

D. \(v_1^2 = v_2^2 + {\omega ^2}\left( {x_2^2 - x_1^2} \right)\).

Lời giải

Đáp án đúng: D

Áp dụng công thức: \({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\)

Tại thời điểm t₁ và t₂:

\(\left\{ \begin{array}{l}x_1^2 + \frac{{v_1^2}}{{{\omega ^2}}} = {A^2}\\x_2^2 + \frac{{v_2^2}}{{{\omega ^2}}} = {A^2}\end{array} \right. \Rightarrow x_1^2 + \frac{{v_1^2}}{{{\omega ^2}}} = x_2^2 + \frac{{v_2^2}}{{{\omega ^2}}}\)

\( \Rightarrow v_1^2 = v_2^2 + {\omega ^2}\left( {x_2^2 - x_1^2} \right)\)