Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Vật lí gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Vật lí. Mời các bạn đón xem:

Top 1000 câu hỏi thường gặp môn Vật lí (Phần 6)

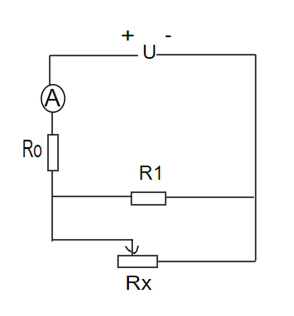
Bài 42: Cho mạch điện: U = 16V , R₀ =4 Ω , R₁ = 12 Ω, R_x là giá trị tức thời của một biến trở đủ lớn, ampe kế A và dây nối có điện trở không đáng kể.

1. Tính R_x sao cho công suất tiêu thụ trên nó bằng 9 W và tính hiệu suất của mạch điện. Biết rằng tiêu hao năng lượng trên R₁, R_x là có ích, trên R₀ là vô ích.

2. Với giá trị nào của R_x thì công suất tiêu thụ trên nó là cực đại? Tính công suất ấy?

Lời giải

Mạch: \({R_0}nt\left( {{R_1}//R{}_x} \right)\)

Đặt R_x = x \(\left( \Omega  \right)\)

\({R_{td}} = {R_0} + \frac{{{R_1}.x}}{{{R_1} + x}} = 4 + \frac{{12x}}{{12 + x}} = \frac{{16x + 48}}{{12 + x}}\)

\( \Rightarrow I = \frac{U}{{{R_{td}}}} = \frac{{16}}{{\frac{{16x + 48}}{{12 + x}}}} = \frac{{12 + x}}{{x + 3}}\)

\({U_{Rx}} = U{}_{R1} = U{}_{R1x} = \frac{{12 + x}}{{x + 3}}.\frac{{12x}}{{12 + x}} = \frac{{12x}}{{x + 3}}\)

Mà \(P = \frac{{U_{Rx}^2}}{{{R_x}}} = 9W \Leftrightarrow \frac{{\frac{{144{x^2}}}{{{{\left( {x + 3} \right)}^2}}}}}{x} = 9 \Rightarrow 9{x^2} - 90x + 81 = 0\)

\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{x = 1 \Rightarrow {R_x} = 1\left( \Omega  \right)}\\{x = 9 \Rightarrow {R_x} = 9\left( \Omega  \right)}\end{array}} \right.\)

Hiệu suất của mạch điện

\(H = \frac{{{P_{1x}}}}{P}.100\%  = \frac{{{I^2}.{R_{1x}}}}{{{I^2}.{R_{td}}}}.100\%  = \frac{{{R_{1x}}}}{{{R_{td}}}}.100\%  = \frac{{3{R_x}}}{{4{R_x} + 12}}.100\% \)

+ R_x = 1\(\left( \Omega  \right)\) \( \Rightarrow H = 18,75\% \)

+ R_x = 9\(\left( \Omega  \right)\)\( \Rightarrow H = 56,25\% \)

b. Từ câu a

\( \Rightarrow {P_{{R_x}}} = \frac{{{U^2}}}{{{R_x}}} = \frac{{{{\left( {\frac{{12x}}{{x + 3}}} \right)}^2}}}{x} = \frac{{144x}}{{{x^2} + 6x + 9}} = \frac{{144}}{{x + \frac{9}{x} + 6}}\)

Để P_Rx max khi \((x + \frac{9}{x} + 6)\,\,\min \)\( \Rightarrow \left( {x + \frac{9}{x}} \right)\,\,\min \)

Áp dụng BĐT Cô – si: \(x + \frac{9}{x} \ge 2\sqrt {x.\frac{9}{x}}  = 6\)

\( \Rightarrow {P_{Rx\,max}} = \frac{{144}}{{6 + 6}} = 12\,\left( W \right)\)