Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Vật lí gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Vật lí. Mời các bạn đón xem:

Top 1000 câu hỏi thường gặp môn Vật lí có đáp án (Phần 26)

Câu 1: Một vật dao động điều hoà dọc theo trục Ox, vận tốc vật khi qua vị trí cân bằng là 62,8 cm/s² và gia tốc cực đại là 2 m/s². Lấy π = 10. Biên độ và chu kì dao động của vật là:

A. A = 10 cm; T = 1 s.

B. A = 1 cm; T = 0,1 s.

C. A = 2 cm; T = 0,2 s.

D. A = 20 cm; T = 2 s.

Lời giải

Đáp án đúng là D

Ta có: \({v_{\max }} = A\omega ;{a_{max}} = A{\omega ^2} \Rightarrow A = \frac{{v_{max}^2}}{{{a_{max}}}} = 20\left( {cm} \right)\)

\(\omega  = \pi  = \frac{{2\pi }}{T}\left( {rad/s} \right) \Rightarrow T = 2\left( s \right)\)

Câu 2: Một điện tích điểm q = 10^-7 C đặt trong điện trường của điện tích điểm Q, chịu tác dụng của lực F = 3.10^-3 N. Cường độ điện trường E tại điểm đặt điện tích q là

A. \({2.10^{ - 4}}\left( {V/m} \right)\).

B. \({3.10^4}\left( {V/m} \right)\).

C. \({4.10^4}\left( {V/m} \right)\).

D. \(2,{5.10^4}\left( {V/m} \right)\).

Lời giải

Đáp án đúng là B

Cường độ điện trường E tại điểm đặt điện tích q là

\(E = \frac{F}{q} = \frac{{{{3.10}^{ - 3}}}}{{{{10}^{ - 7}}}} = {3.10^4}\left( {V/m} \right)\)

Câu 3: Cho phương trình dao động điều hòa $x=cos\left(20\pi t-\frac{\pi }{6}\right)$(cm). Xác định biên độ, chu kì, tần số và pha ban đầu của dao động. Tìm li độ x khi vật đã dao động được nửa chu kì?

Lời giải

Biên độ: A = 1 cm.

Tần số góc: \(\omega  = 20\pi \left( {rad/s} \right) \Rightarrow T = \frac{{2\pi }}{\omega } = 0,1\left( s \right) \Rightarrow f = 10\left( {Hz} \right)\)

Pha ban đầu của dao động: \({\varphi _0} =  - \frac{\pi }{6}\)

Tại t = 0: \(x = \frac{{\sqrt 3 }}{2}\)

Sau một nửa chu kì vật có li độ: \(x =  - \frac{{\sqrt 3 }}{2}\)

Câu 4: Một quả cầu có khối lượng $m=4,{5.10}^{-3}kg$ treo vào sợi dây dài 2 m. Quả cầu nằm trong điện trường có $\overrightarrow{E}$ nằm ngang, hướng sang trái như hình vẽ. Biết $d=1\left(m\right);$ $E=2000\left(V/m\right).$ Lấy $g=10\left(\mathrm{m}/{\mathrm{s}}^2\right).$ Tính độ lớn lực căng dây.

A. 0,09 N.

B. 0,052 N.

C. 0,045 N.

D. 0,156 N.

Lời giải

Đáp án đúng là B

Lực tác dụng vào quả cầu: \(\vec P;{\rm{ }}{\vec F_d};{\rm{ }}\vec T\)

Biểu diễn các lực tác dụng vào quả cầu như hình vẽ.

Khi quả cầu cân bằng: \(\vec P + {\vec F_d} + \vec T = 0\)

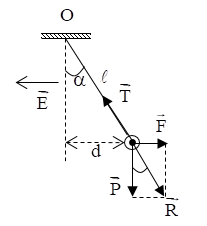
Đặt \(\vec R = \vec P + {\vec F_d} \Rightarrow \vec T + \vec R = 0 \Rightarrow \left\{ \begin{array}{l}\vec T \uparrow  \downarrow \vec R\\T = R\end{array} \right.\)

Từ hình vẽ ta có: \(\cos \alpha  = \frac{{\sqrt {{\ell ^2} - {d^2}} }}{\ell } = \frac{P}{R} \Rightarrow R = \frac{{mg\ell }}{{\sqrt {{\ell ^2} - {d^2}} }} = 0,052\left( N \right)\)

Vậy độ lớn lực căng dây: T = R = 0,052 N.

Câu 5: Hai điện tích điểm q = 2.10^-2 (μC) và q = - 2.10^-2 (μC) đặt tại hai điểm A và B cách nhau một đoạn a = 30 (cm) trong không khí. Lực điện tác dụng lên điện tích q = 2.10^-9 (C) đặt tại điểm M cách đều A và B một khoảng bằng a có độ lớn là:

A. 4.10^-6 N.

B. 5.10^-6 N.

C. 7.10^-6 N.

D. 2.10^-6 N.

Lời giải

Đáp án đúng là A

\({F_{10}} = k\frac{{\left| {{q_1}{q_0}} \right|}}{{{r^2}}} = {4.10^{ - 6}}\left( N \right);{F_{20}} = k\frac{{\left| {{q_2}{q_0}} \right|}}{{{r^2}}} = {4.10^{ - 6}}\left( N \right)\)

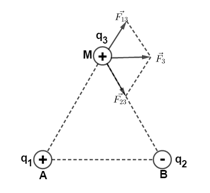
Lực điện tác dụng lên điện tích đặt tại điểm M là\(F_0^2 = F_{10}^2 + F_{20}^2 + 2{F_{10}}.{F_{20}}\cos \alpha  \Rightarrow {F_0} = {4.10^{ - 6}}\left( N \right)\)

Câu 6: Một con lắc lò xo treo thẳng đứng gồm vật nặng có khối lượng m = 100 g và lò xo khối lượng không đáng kể. Chọn gốc toạ độ ở VTCB, chiều dương hướng lên. Biết con lắc dao động theo phương trình: x = 4cos(10t + π/3)cm. Lấy g = 10 m/s². Độ lớn lực đàn hồi tác dụng vào vật tại thời điểm vật đã đi quãng đường s = 3 cm kể từ t = 0 là

A. 1,2 N.

B. 1,1 N.

C. 1,6 N.

D. 0 N.

Lời giải

Đáp án đúng là B

Lò xo treo thẳng đứng. Gốc toạ độ trùng vị trí cân bằng chiều dương hướng lên. Ta có ban đầu vật đang ở li độ x = 2 cm theo chiều âm.

Sau khi đi được quãng đường là s =  3 cm vật đang ở li độ x = -1 theo chiều âm.

Tại vị trí cân bằng lò xo dãn một đoạn: \(\Delta {\ell _0} = \frac{{mg}}{k} = \frac{g}{{{\omega ^2}}} = 0,1\left( m \right)\)

Tại li độ x = -1 cm, lò xo dãn một đoạn: \(\Delta \ell  = \Delta {\ell _0} + \left| x \right| = 0,11\left( m \right)\)

Độ cứng của lò xo: \(k = m{\omega ^2} = 10\left( {N/m} \right)\)

→ Độ lớn lực đàn hồi khi vật đi được quãng đường s = 3 cm là: F = k.Δl = 1,1 N

Câu 7: Một con lắc đơn dao động điều hòa với phương trình li độ góc $\alpha =0,1\cos \left(2\pi t\right)rad.$ Lấy $g=10\left(m/s^2\right)$ và ${\pi }^2=10.$ Khi qua vị trí cân bằng vật có tốc độ là

A. $20\pi$ cm/s.

B. 5\(\pi \) cm/s.

C. 50 cm/s.

D. 0,2\(\pi \) cm/s.

Lời giải

Đáp án đúng là B

\[\omega  = \sqrt {\frac{g}{\ell }}  \Rightarrow \ell  = 25\,cm\]

Qua vị trí cân bằng có tốc độ cực đại: \({v_{max}} = \omega {s_0} = \omega {\alpha _0}\ell  \Rightarrow {v_{max}} = 5\pi \) cm/s

Câu 8: Một người đi xe đạp trên đoạn đường MN. Trên nửa đầu của đoạn MN đi với tốc độ 20 km/h. Trên nửa còn lại thì 1/2 thời gian đầu đi với tốc độ 10 km/h; trên 1/2 thời gian còn lại đi với tốc độ 5 km/h. Tính tốc độ trung bình trên đoạn MN. 

Lời giải

Gọi t là thời gian đi cả đoạn đường MN.

Thời gian đi nửa đầu đoạn MN: \({t_1} = \frac{{MN}}{{2.{v_1}}} = \frac{{MN}}{{2.20}} = \frac{{{\rm M}N}}{{40}}\left( h \right)\)

Thời gian đi nửa đoạn đường còn lại là: \({t_2}\)

Trên nửa còn lại:

+ Quãng đường người này đi trong ½ thời gian đầu: \({s_2} = {v_2}t' = 10.\frac{{{t_2}}}{2} = 5{t_2}\left( {km} \right)\)

+ Quãng đường người này đi trong ½ thời gian còn lại: \({s_3} = {v_3}t'' = 5.\frac{{{t_2}}}{2} = 2,5{t_2}\left( {km} \right)\)

+ Mà \({s_2} + {s_3} = \frac{{MN}}{2} \Rightarrow 5{t_2} + 2,5{t_2} = \frac{{MN}}{2} \Rightarrow {t_2} = \frac{{MN}}{{15}}\left( h \right)\)

Tốc độ trung bình trên cả đoạn đường MN:

\({v_{tb}} = \frac{s}{t} = \frac{{{s_1} + {s_2} + {s_3}}}{{{t_1} + {t_2}}} = \frac{{MN}}{{\frac{{MN}}{{40}} + \frac{{MN}}{{15}}}} = \frac{{120}}{{11}}\left( {km/h} \right)\)

Câu 9: Bạn Việt đi xe đạp đến trường theo đường thẳng như hình vẽ. Khi đến quầy bán báo, bạn sực nhớ đã quên một cuốn sách ở nhà nên quay về nhà lấy sách rồi lại đạp xe đến trường. Độ dời khi bạn quay từ quầy báo về nhà và độ dời khi bạn từ quầy báo đến trường lần lượt là:

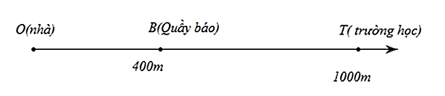
A. 400 m và 600 m.

B. 400 m và 1000 m.

C. - 400 m và 1000 m.

D. - 400 m và 600 m.

Lời giải

Đáp án đúng là D

Ta có: Độ dời khi bạn Việt từ quầy báo về nhà:

\({s_2} = \overline {BO}  =  - \overline {OB}  =  - {x_B} =  - 400\left( m \right)\)

Độ dời khi bạn Việt từ quầy báo đến trường:

\({s_3} = \overline {BT}  = {x_T} - {x_B} = 1000 - 400 = 600\left( m \right)\)

Câu 10: Đặt điện áp u = U cos ωt (U và ω không đổi) vào hai đầu đoạn mạch AB theo thứ tự gồm một tụ điện, một cuộn cảm thuần và một điện trở thuần mắc nối tiếp. Gọi M là điểm nối giữa tụ điện và cuộn cảm. Biết điện áp hiệu dụng giữa hai đầu AM bằng điện áp hiệu dụng giữa hai đầu MB và cường độ dòng điện trong đoạn mạch lệch pha π/12 so với điện áp giữa hai đầu đoạn mạch. Hệ số công suất của đoạn mạch MB là

A. \(\frac{{\sqrt 3 }}{2}\).

B. 0,75.

C. 0,5.

D. \(\frac{{\sqrt 2 }}{2}\).

Lời giải

Đáp án đúng là C

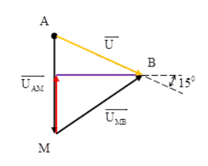
\({U_{MA}} = {U_{MB}}\) nên AMB là tam giác cân tại M, do vậy \(\widehat A = \widehat B\)

Mặt khác: \(\widehat A + {15^0} = {90^0}\)

Từ đó, ta tìm được: \(\widehat A = {75^0} \Rightarrow {\varphi _{MB}} = {75^0} - {15^0} = {60^0}\)

\(\cos {\varphi _{MB}} = 0,5\)

Câu 11: Một chất điểm chuyển động với đồ thị vận tốc theo – thời gian được cho như hình vẽ. Tốc độ trung bình của chất điểm trong khoảng thời gian 10 s đầu tiên là?

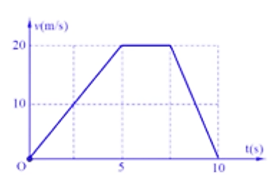
Lời giải

Quãng đường chất điểm đi được trong 10 s đầu: \(s = \frac{{\left( {2,5 + 10} \right).20}}{2} = 125\left( m \right)\)

Tốc độ trung bình của chất điểm trong khoảng thời gian 10 s đầu tiên là:

\({v_{tb}} = \frac{s}{t} = \frac{{125}}{{10}} = 12,5\left( {m/s} \right)\)

Câu 12: Để xác định gia tốc a của một chuyển động thẳng biến đổi đều, một học sinh đã sử dụng đồng hồ bấm giờ và thước mét để xác định thời gian t và đo quãng đường L, sau đó xác định a bằng công thức \(L = a\frac{{{t^2}}}{2}\).

Kết quả cho thấy \(L = \left( {2 \pm 0,005} \right)\left( m \right);t = \left( {4,2 \pm 0,2} \right)\left( s \right).\) Xác định gia tốc a và sai số tuyệt đối của nó.

Lời giải

\(L = \frac{{a{t^2}}}{2} \Rightarrow \overline a  = \frac{{2\overline L }}{{{{\left( {\overline t } \right)}^2}}} = \frac{{2.2}}{{4,{2^2}}} = 0,23\left( {{\rm{m/}}{{\rm{s}}^2}} \right)\)

\(L = a\frac{{{t^2}}}{2} \Rightarrow a = \frac{{2L}}{{{t^2}}} \Rightarrow \frac{{\Delta a}}{{\overline a }} = \frac{{\Delta L}}{{\overline L }} + 2\frac{{\Delta t}}{{\overline t }} = \frac{{0,005}}{2} + 2.\frac{{0,2}}{{4,2}} \approx 0,098\)

\( \Rightarrow \Delta a = 0,098.\overline a  = 0,023\left( {m/{s^2}} \right)\)

Vậy \(a = 0,23 \pm 0,02\left( {m/{s^2}} \right)\)

Câu 13: Một sóng ngang truyền trên sợi dây đàn hồi rất dài với tốc độ v = 0,5 m/s, chu kỳ dao động là T = 10 (s). Khoảng cách giữa 2 điểm gần nhau nhất dao động vuông pha là

A. 2,5 m.

B. 20 m.

C. 1,25 m.

D. 0,05 m.

Lời giải

Đáp án đúng là C

Khoảng cách giữa hai điểm gần nhau nhất dao động vuông pha trên cùng một phương truyền sóng ngang là \(\frac{\lambda }{4} = 1,25\left( m \right)\)

Câu 14: Chọn phát biểu Sai khi nói về dao động điều hòa.

A. Trong dao động điều hòa cứ sau một chu kỳ vật lại có tốc độ như cũ.

B. Li độ của vật dao động điều hòa là tọa độ của vật trong hệ tọa độ có gốc là vị trí cân bằng.

C. Chu kỳ dao động điều hòa là thời gian ngắn nhất sau đó vật trở về vị trí ban đầu.

D. Dao động điều hòa là dao động trong đó li độ của vật là một hàm cosin hay sin của thời gian.

Lời giải

Đáp án đúng là C

Chu kỳ dao động là thời gian ngắn nhất sau đó vật lặp trạng thái dao động ở vị trí cũ chứ không phải là vị trí ban đầu (t = 0). Vì có thể vị trí ban đầu là ở O nhưng vị trí mà chúng ta tính chu kỳ bắt đầu là ở biên. Nên đáp án sai là C.

Câu 15: Một con lắc đơn dao động điều hòa với biên độ góc là 9⁰ và năng lượng dao động là 0,02 J thì động năng của con lắc ở li độ góc 4,5⁰ là:

A. 0,198 J.

B. 0,027 J.

C. 0,015 J.

D. 0,225 J.

Lời giải

Đáp án đúng là C

Tại vị trí \(\alpha  = 4,{5^0} = \frac{{{\alpha _0}}}{2} \Rightarrow {{\rm{W}}_t} = \frac{{\rm{W}}}{4} \Rightarrow {{\rm{W}}_d} = \frac{3}{4}{\rm{W}} = 0,015\left( J \right)\)

Câu 16: Một êlectron di chuyển trong điện trường đều \(\vec E\) một đoạn 0,6 cm, từ điểm M đến điểm N dọc theo một đường sức điện thì lực điện sinh công 9,6.10⁻¹⁸ J. Tính công mà lực điện sinh ra khi êlectron di chuyển tiếp 0,4 cm từ điểm N đến điểm P theo phương và chiều nói trên.

Lời giải

Do electron di chuyển dọc theo đường sức điện nên lực điện và hướng dịch chuyển hợp với nhau góc 180⁰

A = qEd ; trong đó A = 9,6.10⁻¹⁸J ; q = -e = -1,6.10⁻¹⁹ C ; d = -0,6 cm.

Suy ra E = 1.10⁴ V/m.

Công của lực điện khi electron di chuyển đoạn NP dài 0,4 cm (d' = - 0,4 cm) là 6,4.10⁻¹⁸ J.

Câu 17: Đồ thị vận tốc – thời gian của một chuyển động thẳng được biểu diễn như hình vẽ. Hãy cho biết trong những khoảng thời gian nào vật chuyển động chậm dần đều?

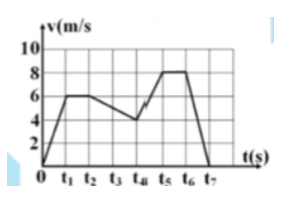
A. Từ t = 0 đến t₁ và từ t₄ đến t₅.

B. Từ t₁ đến t₂ và từ t₅ đến t₆.

C. Từ t₂ đến t₄ và từ t₆ đến t₇.

D. Từ t₁ đến t₂ và từ t₄ đến t₅.

Lời giải

Đáp án đúng là C

Trong chuyển động thẳng chậm dần đều thì đồ thị vận tốc - thời gian là đường chéo xuống.  

Câu 18: Từ hai điểm A và B cách nhau 200 cm hai vật chuyển động ngược chiều nhau. Vật thứ nhất từ A bắt đầu chuyển động nhanh dần đều với gia tốc 3 cm/s², cùng lúc vật thứ hai đi ngang qua B với vận tốc 5 cm/s và chuyển động nhanh dần đều với gia tốc 2 cm/s². Hãy xác định thời gian và vị trí hai vật gặp nhau?

A. 8 s, cách A 96 cm.

B. 8 s, cách B 96 cm.

C. 15,6 s, cách A 365 cm.

D. 15,6 s, cách B 365 cm.

Lời giải

Đáp án đúng là A

Chọn trục Ox trùng AB, chiều dương từ A đến B, gốc tọa độ tại A, gốc thời gian là lúc hai xe bắt đầu chuyển động.

Phương trình chuyển động của hai xe là: \(\left\{ \begin{array}{l}{x_1} = 0 + 0t + \frac{1}{2}3.{t^2} = 1,5{t^2}\left( {cm} \right)\\{x_2} = 200 - 5t + \frac{1}{2}\left( { - 2} \right).{t^2} = 200 - 5t - {t^2}\left( {cm} \right)\end{array} \right.\)

Hai xe gặp nhau khi: \({x_1} = {x_2} \Leftrightarrow 1,5{t^2} = 200 - 5t - {t^2}\)\( \Leftrightarrow 2,5{t^2} + 5t - 200 = 0 \Rightarrow t = 8\left( s \right)\)

Vị trí gặp nhau cách A: \({x_1} = 96\left( {cm} \right)\)

Câu 19: Hai lực có giá đồng quy có độ lớn 7 N và 13 N. Độ lớn hợp lực của hai lực này không thể có giá trị nào sau đây?

A. 7 N.

B. 13 N.

C. 20 N.

D. 22 N.

Lời giải

Đáp án đúng là D

Hợp lực của hai lực đồng quy luôn có độ lớn thỏa mãn:

\(\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2} \Rightarrow 6 \le F \le 20\)

Suy ra F không thể là 22 N

Câu 20: Một chất điểm dao động điều hòa có phương trình vận tốc$v=126\cos \left(5\pi t+\frac{\pi }{3}\right)$ cm/s, t tính bằng s. Vào thời điểm nào sau đây vật sẽ đi qua vị trí có li độ 4 cm theo chiều âm của trục tọa độ?  

A. 0,1 s.     

B. 0,3 s.       

C. 0,33 s.       

D. 0,17 s.

Lời giải

Đáp án đúng là A

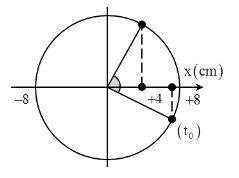
+ Phương trình li độ của vật \(x = 8\sin \left( {5\pi t + \frac{\pi }{3}} \right) = 8\cos \left( {5\pi t - \frac{\pi }{6}} \right)\)cm.

+ Tại t = 0 vật đi qua vị trí \(x = \frac{{\sqrt 3 }}{2}A = 4\sqrt 3 \)cm theo chiều dương.

Biễu diễn các vị trí tương ứng trên đường tròn, ta thu được: Δt = 0,25T = 0,1 s.  

Câu 21: Trong mạch chọn sóng của máy thu vô tuyến có mạch dao động gồm cuộn cảm thuần có độ tự cảm L = 0,2 mH và một tụ điện có điện dung thay đổi từ 50 pF đến 450 pF. Máy có thể thu được các sóng vô tuyến trong dải sóng từ:

A. 168 m đến 600 m.

B. 176 m đến 625 m.

C. 200 m đến 824 m.

D. 188 m đến 565 m.

Lời giải

Đáp án đúng là D

Ta có: \(\lambda  = 2\pi c\sqrt {LC} \)

Thay L = 0,2 mH; C₁ = 50 pF: \({\lambda _1} = 2\pi c\sqrt {L{C_1}}  = 2\pi {.3.10^8}\sqrt {0,{{2.10}^{ - 3}}{{.50.10}^{ - 12}}}  \approx 188\,m\)

Thay L = 0,2 mH; C₂ = 50 pF: \({\lambda _2} = 2\pi c\sqrt {L{C_2}}  = 2\pi {.3.10^8}\sqrt {0,{{2.10}^{ - 3}}{{.450.10}^{ - 12}}}  \approx 565\,m\)

Thay số ta được: \(\lambda  \in \left[ {188;565} \right]\left( m \right)\)

Câu 22: Một vật dao động điều hòa với phương trình $x=\sqrt{2}\cos \left(2\pi t+\frac{\pi }{3}\right)$cm thì chịu tác dụng của ngoại lực cưỡng bức $F=\sqrt{2}\cos \left(\omega t-\frac{\pi }{6}\right)\left(N\right).$ Để biên độ dao động là lớn nhất thì tần số của lực cưỡng bức phải bằng

A. 2π Hz.

B. π Hz.

C. 1 Hz.

D. 2 Hz.

Lời giải

Đáp án đúng là C

Để biên độ dao động cưỡng bức là lớn nhất thì \({f_F} = {f_0} = 1\left( {Hz} \right)\).

Câu 23: Trên một sợi dây dài có sóng ngang hình sin truyền qua. Hình dạng của một đoạn dây tại hai thời điểm t₁ và t₂ có dạng như hình vẽ bên. Trục Ou biểu diễn li độ của các phần tử M và N ở các thời điểm. Biết t₂ − t₁ = 0,11 s, nhỏ hơn một chu kì sóng. Chu kì dao động của sóng có giá trị là

A. 0,4 s.

B. 1,2 s.

C. 0,5 s.

D. 0,6 s.

Lời giải

Đáp án đúng là C

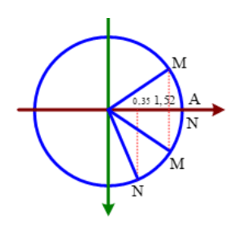
Trong cùng khoảng thời gian, \({t_2} - {t_1}\), điểm N từ vị trí 0,35 đến biên A, còn M vẫn có li độ 1,52 nên nó đi từ li độ 1,52 đến biên rồi quay về 1,52. Biểu diễn li độ của M và N theo thời gian:

Từ hình vẽ ta được:

\(\cos \alpha  = \frac{{0,35}}{A};\cos \frac{\alpha }{2} = \frac{{1,52}}{A}\)

Từ hai phương trình trên ta tính được góc \(\alpha  = {8^0}\)ứng với \(\frac{{11}}{{50}}T\)

Vậy 0,11 = \(\frac{{11}}{{50}}T \Rightarrow T = 0,5\left( s \right)\).

Câu 24: Một con lắc lò xo gồm một lò xo nhẹ và một vật nặng có khối lượng m. Con lắc dao động điều hòa với chu kì T₁. Thay vật m bằng vật có khối lượng m và gắn vào lò xo nói trên thì hệ dao động điều hòa với chu kì T₂. Nếu chỉ gắn vào lò xo ấy một vật có khối lượng \[m = 2{m_1} + 3{m_2}\]thì hệ dao động điều hòa với chu kì bằng

A. \(\sqrt {3T_1^2 + 2T_2^2} \).

B. \(\sqrt {\frac{{T_1^2}}{2} + \frac{{T_2^2}}{3}} \).

C. \(\sqrt {2T_1^2 + 3T_2^2} \).

D. \(\sqrt {\frac{{T_1^2}}{3} + \frac{{T_2^2}}{2}} \).

Lời giải

Đáp án đúng là C

Ta có: \(T = 2\pi \sqrt {\frac{m}{k}}  \Rightarrow {T^2} \sim m\)

Khi \[m = 2{m_1} + 3{m_2}\]\( \Rightarrow {T^2} = 2T_1^2 + 3T_2^2 \Rightarrow T = \sqrt {2T_1^2 + 3T_2^2} \)

Câu 25: Một sóng ngang truyền trên một sợi dây đàn hồi rất dài với tốc độ truyền sóng 0,2 m/s, chu kì đao động là 10 s. Khoảng cách giữa 3 điểm liên tiếp trên dây dao động ngược pha nhau là:

A. 4 m.

B. 1 m.

C. 0,5 m.

D. 2 m.

Lời giải

Đáp án đúng là D

Bước sóng: λ = vT = 2 (m)

Khoảng cách giữa 3 điểm liên tiếp dao động ngược pha là:

X = 2. \(\frac{\lambda }{2}\) = λ = 2 (m).

Câu 26: Hành khách trên tàu A thấy tàu B đang chuyển động về phía trước. Còn hành khách trên tàu B lại thấy tàu C cũng đang chuyển động về phía trước. Vậy hành khách trên tàu A sẽ thấy tàu C:

A. Đứng yên.

B. Chạy lùi về phía sau.

C. Tiến về phía trước.

D. Tiến về phía trước rồi sau đó lùi về phía sau.

Lời giải

Đáp án đúng là C

Hành khách trên tàu A thấy tàu B đang chuyển động về phía trước.

Còn hành khách trên tàu B lại thấy tàu C cũng đang chuyển động về phía trước.

Vậy hành khách trên tàu A sẽ thấy tàu C tiến về phía trước.

Câu 27: Một hạt bụi tích điện có khối lượng m = 10^-8g nằm cân bằng trong điện trường đều có hướng thẳng đứng xuống dưới và có cường độ E = 1 000 V/m, lấy g = 10 m/s². Điện tích của hạt bụi là

A. -10^-13 C.

B. 10^-13 C.

C. -10^-10 C.

D. 10^-10 C.

Lời giải

Đáp án đúng là A

Hạt bụi nằm cân bằng nên F_đ hướng lên => q < 0

F_đ = P <=> |q|E = mg <=> |q|.1000 = 10^-8.10^-3.10 <=> q = -10^-13 C

Câu 28: Ở mặt thoáng của một chất lỏng, tại hai điểm A và B cách nhau 20 cm có hai nguồn sóng dao động điều hòa theo phương thẳng đứng, cùng pha, cùng biên độ và cùng tần số 50 Hz. Coi biên độ sóng không đổi khi sóng truyền đi. Tốc độ truyền sóng trên mặt chất lỏng là 3 m/s. Trên đoạn thẳng AB, số điểm dao động có biên độ cực đại là

A. 7.                       B. 6.                       C. 8.                       D. 9.

Lời giải

Đáp án đúng là A

Ta có: \(\lambda  = \frac{v}{f} = \frac{{300}}{{50}} = 6\left( {cm} \right)\)

Số điểm dao động với biên độ cực đại, ta có:

- AB < kλ < AB  <=> -20 < 6k < 20  <=> - 3,3 < k < 3,3

Suy ra trên AB có 7 cực đại.

Câu 29: Một hạt bụi tích điện có khối lượng m = 3.10^-6g nằm cân bằng trong điện trường đều thẳng đứng hướng xuống có cường độ E = 2000 V/m. Lấy g = 10 m/s². Điện tích hạt bụi là?

Lời giải

Ta có: \(\vec P \uparrow  \uparrow {\vec F_d}\)

⇒ \({\vec F_d}\)hướng xuống và ngược chiều với \(\vec E \Rightarrow q < 0\)

Vì hạt bụi nằm cân bằng trong điện trường đều nên ta có:

\({F_d} = P \Leftrightarrow E\left| q \right| = mg \Rightarrow q =  - 1,{5.10^{ - 11}}C\)

Câu 30: Điện tích q = 10^-8 C di chuyển dọc theo các cạnh của tam giác đều ABC cạnh a = 10 cm trong điện trường đều cường độ điện trường là E = 300 V/m, \(\vec E//BC\). Tính công của lực điện trường khi q di chuyển trên mỗi cạnh của tam giác:

A. \({A_{AB}} = 1,{5.10^{ - 7}}\left( J \right);{A_{BC}} =  - {3.10^{ - 7}}\left( J \right);{A_{AC}} = 1,{5.10^{ - 7}}\left( J \right)\).

B. \({A_{AB}} = 1,{5.10^{ - 7}}\left( J \right);{A_{BC}} = {3.10^{ - 7}}\left( J \right);{A_{AC}} =  - 1,{5.10^{ - 7}}\left( J \right)\).

C. \({A_{AB}} =  - 1,{5.10^{ - 7}}\left( J \right);{A_{BC}} = {3.10^{ - 7}}\left( J \right);{A_{AC}} = 1,{5.10^{ - 7}}\left( J \right)\).

D. \({A_{AB}} =  - 1,{5.10^{ - 7}}\left( J \right);{A_{BC}} = {3.10^{ - 7}}\left( J \right);{A_{AC}} =  - 1,{5.10^{ - 7}}\left( J \right)\).

Lời giải

Đáp án đúng là C

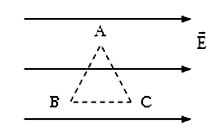
Công của lực điện trường khi q di chuyển trên cạnh AB là:

\({A_{AB}} = q.E.AB.\cos {120^0} =  - 1,{5.10^{ - 7}}\left( J \right)\)

Công của lực điện trường khi q di chuyển trên cạnh BC là:

\({A_{BC}} = q.E.BC = {3.10^{ - 7}}\left( J \right)\)

Công của lực điện trường khi q di chuyển trên cạnh AC là:

\({A_{AC}} = q.E.AC.\cos {60^0} = 1,{5.10^{ - 7}}\left( J \right)\)

Câu 31: Một sợi dây đàn hồi căng ngang, dài 60 cm, hai đầu cố định. Trên dây đang có sóng dừng với 3 bụng sóng, tần số sóng là 100 Hz. Tốc độ truyền sóng trên dây là 

A. 20 m/s.

B. 400 m/s.

C. 200 m/s.

D. 40 m/s.

Lời giải

Đáp án đúng là D

Bước sóng: \(\lambda  = \frac{{2\ell }}{k} = \frac{{2.60}}{3} = 40\left( {cm} \right) = 0,4\left( m \right)\)

Tốc độ truyền sóng trên dây:

\(v = \lambda .f = 0,4.100 = 40\left( {m/s} \right)\)

Câu 32: Trong thí nghiệm giao thoa sóng trên mặt nước, tốc độ truyền sóng là 0,5 m/s, cần rung có tần số 40 Hz. Khoảng cách giữa hai điểm cực đại giao thoa cạnh nhau trên đoạn thẳng S₁S₂.

A. 2,5 cm.

B. 1,25 cm.

C. 0,625 cm.

D. 0,3125 cm.

Lời giải

Đáp án đúng là C

Bước sóng: \(\lambda  = \frac{v}{f} = \frac{{0,5}}{{40}} = 0,0125\left( m \right) = 1,25\left( {cm} \right)\)

Khoảng cách giữa 2 cực đại liên tiếp: \(\frac{\lambda }{2} = 0,625\left( {cm} \right)\)

Câu 33: Chu kì dao động điều hòa của một con lắc đơn có chiều dài dây treo l tại nơi có gia tốc trọng trường g là

A. \(T = \frac{1}{{2\pi }}\sqrt {\frac{\ell }{g}} \).

B. \(T = 2\pi \sqrt {\frac{g}{\ell }} \).

C. \(T = 2\pi \sqrt {\frac{\ell }{g}} \).

D. \(T = \frac{1}{{2\pi }}\sqrt {\frac{g}{\ell }} \).

Lời giải

Đáp án đúng là C

Chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{\ell }{g}} \).

Câu 34: Một vật dao động điều hòa dọc theo trục Ox. Vận tốc của vật khi đi qua vị trí cân bằng là 62,8 cm/s và gia tốc ở vị trí biên là 200 cm/s². Lấy π² = 10. Chu kì dao động của vật là 

A. 2 s. 

B. 0,2 s.   

C. 3,18 s.

D. 0,318 s.

Lời giải

Đáp án đúng là A

Ta có: \(\omega  = \frac{{{a_{max}}}}{{{v_{max}}}} = \frac{{200}}{{62,8}} = \pi \left( {rad/s} \right)\) \( \Rightarrow T = \frac{{2\pi }}{\omega } = 2\left( s \right)\)

Câu 35: Một vật có khối lượng m = 500 g, thực hiện đồng thời hai dao động điều hoà cùng phương, cùng tần số có phương trình: x₁ = 8cos(2πt + $\frac{\pi }{2}$) và x₂ = 8cos(2πt). Động năng của vật khi qua li độ x = $\frac{A}{2}$ là bao nhiêu?

Lời giải

Phương trình dao động tổng hợp: \(x = {x_1} + {x_2} = 8\sqrt 2 \cos \left( {2\pi t + \frac{\pi }{4}} \right)\)

Tại vị trí có: \(x = \frac{A}{2} \Rightarrow {{\rm{W}}_t} = \frac{1}{4}{\rm{W}} \Rightarrow {{\rm{W}}_d} = \frac{3}{4}{\rm{W}} = \frac{3}{4}.\frac{1}{2}.m{\omega ^2}{A^2} = 0,096\left( J \right)\)

Câu 36: Lực có môđun 30 N là hợp lực của hai lực nào?

A. 12 N, 12 N.

B. 16 N, 10 N.

C. 16 N, 46 N.

D. 16 N, 50 N.

Lời giải

Đáp án đúng là C

Ta có, điều kiện của hợp lực: |F₁−F₂| ≤ F ≤ F₁ + F₂

Phương án A: 0 ≤ F ≤ 24 N.

Phương án B: 6 N ≤ F ≤ 26 N.

Phương án C: 30 N ≤ F ≤ 62 N.

Phương án D: 34 N ≤ F ≤ 66 N.

=> Lực có môđun 30 N là hợp lực của hai lực thành phần 16 N và 46 N có cùng phương nhưng ngược chiều.

Câu 37: Chọn câu trả lời sai. Năng lượng của sóng truyền từ một nguồn điểm sẽ:

A. Giảm tỉ lệ với bình phương quãng đường truyền sóng, khi truyền trong không gian.

B. Giảm tỉ lệ với quãng đường truyền sóng, khi môi trường truyền là một đường thẳng.

C. Giảm tỉ lệ với quãng đường truyền sóng, khi truyền trên mặt thoáng của chất lỏng.

D. Luôn không đổi khi môi trường truyền sóng là một đường thẳng.

Lời giải

Đáp án đúng: B

B - sai vì: Năng lượng sóng luôn không đổi khi môi trường truyền sóng là 1 đường thẳng.

Câu 38: Có một số điện trở r = 5Ω. Hỏi phải dùng tối thiểu bao nhiêu điện trở đó để mắc thành mạch điện có điện trở 3Ω. Xác định số điện trở r?

 

A. 4.                       B. 5.                       C. 6.                       D. 7.

Lời giải

Đáp án đúng là A

Gọi điện trở của mạch là R → R = 3 Ω

Vì R <  r nên các điện trở r phải được mắc song song.

Giả sử mạch này gồm 1 điện trở r mắc song song với một mạch nào đó có điện trở X.

Ta có: \(\frac{1}{R} = \frac{1}{r} + \frac{1}{X} \Rightarrow X = 7,5\Omega \)

Với \(X = 7,5\Omega  > R = 3\Omega  \Rightarrow \)phải mắc nối tiếp điện trở r với điện trở Y nào đó.

Ta có: \(X = r + Y \Rightarrow Y = 2,5\Omega \)

Vì \(Y = 2,5\Omega  < R = 3\Omega  \Rightarrow \) mắc song song với Z 

Vậy phải có tối thiểu 4 điện trở r.

Câu 39: Trong các phân xưởng dệt, người ta thường treo các tấm kim loại nhiễm điện ở trên cao. Việc làm này có tác dụng gì?

A. Việc làm này có tác dụng hút các bụi bông lên bề mặt của chúng, làm cho không khí trong xưởng tăng bụi hơn.

B. Việc làm này có tác dụng đẩy các bụi bông lên bề mặt của chúng, làm cho không khí trong xưởng ít bụi hơn.

C. Việc làm này có tác dụng hút các bụi bông lên bề mặt của chúng.

D. Việc làm này có tác dụng hút các bụi bông lên bề mặt của chúng, làm cho không khí trong xưởng ít bụi hơn.

Lời giải

Đáp án đúng là D

Việc làm này có tác dụng hút các bụi bông lên bề mặt của chúng, làm cho không khí trong xưởng ít bụi hơn.

Câu 40: Tại nơi có gia tốc trọng trường g, một con lắc đơn dao động điều hòa với biên độ góc α₀ nhỏ. Lấy mốc thế năng ở vị trí cân bằng. Khi con lắc chuyển động nhanh dần theo chiều dương đến vị trí có động năng bằng thế năng thì li độ góc α của con lắc bằng

A. \(\frac{{{\alpha _0}}}{{\sqrt 3 }}\).

B. \(\frac{{{\alpha _0}}}{{\sqrt 2 }}\).

C. \( - \frac{{{\alpha _0}}}{{\sqrt 2 }}\).

D. \( - \frac{{{\alpha _0}}}{{\sqrt 3 }}\).

Lời giải

Đáp án đúng là C

Khi con lắc chuyển động nhanh dần theo chiều dương đến vị trí có động năng bằng thế năng thì li độ góc α của con lắc bằng\( - \frac{{{\alpha _0}}}{{\sqrt 2 }}\).

Câu 41: Đặt điện áp xoay chiều u = 200cos(100πt + π/4) V vào hai đầu đoạn mạch gồm cuộn cảm thuần có độ tự cảm L thay đổi được, điện trở và tụ điện mắc nối tiếp theo thứ tự. Điều chỉnh L thì thấy điện áp hiệu dụng giữa hai đầu cuộn cảm đạt giá trị cực đại bằng 200\(\sqrt 2 \) V. Khi đó, điện áp giữa hai đầu tụ điện có biểu thức là

A. u_C = 100\(\sqrt 2 \)cos100πt (V).

B. u_C = 100\(\sqrt 2 \)cos(100πt – π/2) (V).    

C. u_C = 300cos(100πt – π/2) (V).

D. u_C = 300 cos(100πt – 5π/12) (V).

Lời giải

Đáp án đúng là D

Bài toán L thay đổi để U_L max khi: \({Z_L} = \frac{{{R^2} + Z_C^2}}{{{Z_C}}}\)

Khi đó: \({U_{Lmax}} = \frac{{U\sqrt {{R^2} + Z_C^2} }}{R} \Rightarrow Z_C^2 = 3{R^2} \Rightarrow {Z_L} = \frac{4}{{\sqrt 3 }}R\)

Điện trở của mạch: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}  = \frac{2}{{\sqrt 3 }}R\)

Ta có: \(\frac{{{U_C}}}{U} = \frac{{{Z_C}}}{Z} = \frac{1}{2} \Rightarrow {U_{OC}} = \frac{1}{2}{U_0} = 100\left( V \right)\)

Độ lệch pha giữa u và i là : \(\tan \varphi  = \frac{{{Z_L} - {Z_C}}}{R} = \sqrt 3  \Rightarrow \varphi  = \frac{\pi }{6} \Rightarrow {\varphi _i} = \frac{\pi }{{12}}\)

Vì u_C chậm pha hơn i một góc \(\frac{\pi }{2}\)nên φ_C =\(\frac{{ - 5\pi }}{{12}}\).