Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Vật lí gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Vật lí. Mời các bạn đón xem:

Top 1000 câu hỏi thường gặp môn Vật lí (Phần 9)

Bài 1: Cho cơ hệ như hình vẽ: m₁ = 1 kg; m₂ = 3 kg; hệ số ma sát trượt giữa hai vật và mặt sàn là μ = 0,1; dây nối nhẹ, không giãn. Kéo vật m1 bằng một lực F = 5N hợp với phương ngang góc α = 30°. Lấy g = 10 m/s². Tìm lực căng của dây nối hai vật.

A. 3,75 N.                                                  

B. 5,13 N.

C. 4,5 N.                                                              

D. 2,25 N.

Lời giải:

Đáp án B.

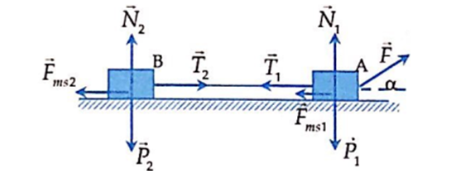
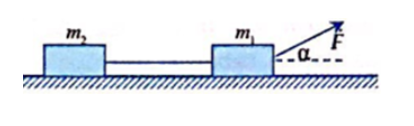
Áp dụng định luật II Niu-tơn cho hệ vật:

$a=\frac{F\cos \alpha -F_{ms1}-F_{ms2}}{m_1+m_2}=\frac{F\cos \alpha -\mu N_1-\mu N_2}{m_1+m_2}$

Ta có: \({N_1} = {m_1}g - F\sin \alpha ;{N_2} = {m_2}g\)

$a=\frac{F\cos \alpha -\mu g(m_1-F\sin \alpha +m_2)}{m_1+m_2}\approx 0,71m/s^2$

Áp dụng định luật II Newton

vật \({m_2}\):\[T - {F_{ms2}} = {m_2}a \Rightarrow T = {m_2}\left( {\mu g + a} \right) = 5,13N\]

Bài 2: Cho hệ như hình vẽ, m₁ = 1 kg, m₂ = 2 kg. Khối lượng ròng rọc và dây không đáng kể, bỏ qua ma sát. Tính sức căng của dây nối, \(g = 10m/{s^2}\)

A. 15,2 N

B. 13,3 N

C. 17 N

D. 15 N

Lời giải:

Đáp án B

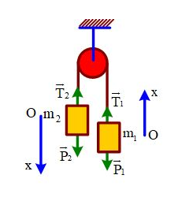
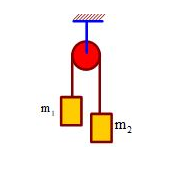
Ta có:

\[{P_1} = {m_1}g = 10\,N\]

\[{P_2} = {m_2}g = 20N\]

\[ \Rightarrow {P_2} > {P_1}\]

Vậy vật m₂ đi xuống vật m₁ đi lên

Chọn chiều dương là chiều chuyển động

Theo định lụât II Niu−Tơn ta có

Vì dây không dãn nên ta có 

$\overrightarrow{P_1}+\overrightarrow{T_1}=m_1\overrightarrow{a}$

$\overrightarrow{P_2}+\overrightarrow{T_2}=m_2\overrightarrow{a}$

\[{T_1} = {T_2} = T\]

Chiếu lên chiều chuyển động

\[T - {P_1} = {m_1}a\]

\[{P_2} - T = {m_2}a\]

\[ \Rightarrow a = \frac{{{P_2} - {P_1}}}{{{m_1} + {m_2}}} = 3,3m/{s^2}\]

\[ \Rightarrow {T_1} = {P_1} + {m_1}a = 13,3\,N = {T_2}\]

Bài 3: Một mạch điện có sơ đồ như hình 11.1, trong đó nguồn điện có suất điện động E = 6 (V) và điện trở trong r = 2 Ω, các điện trở R₁ = 5 Ω, R₂ = 10 Ω và R₃ = 3 Ω.

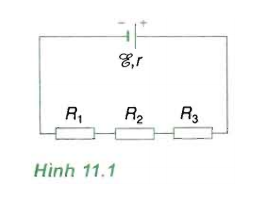
a. Tính điện trở RN  của mạch ngoài.

b. Tính cường độ dòng điện I chạy qua nguồn điện và hiệu điện thế mạch ngoài U.

c. Tính hiệu điện thế U₁ giữa hai đầu điện trở R₁.

Lời giải:

Mạch gồm R₁ nt R₂ nt R₃;

a. Điện trở của mạch ngoài là: R_N = R₁ + R₂ + R₃ = 5 + 10 + 3 = 18 Ω.

b. Áp dụng định luật Ôm cho toàn mạch, ta có:

Cường độ dòng điện chạy qua nguồn điện là: \[I = \frac{{\rm{E}}}{{{R_N} + r}} = \frac{6}{{2 + 18}} = 0,3\,A\]

Hiệu điện thế mạch ngoài là: U  = I.R_N = 0,3.18 = 5,4 (V).

c. Hiệu điện thế giữa hai đầu điện trở R₁ là: U₁ = I.R₁ = 0,3.5 = 1,5 (V).

Bài 4:

BÁO CÁO THỰC HÀNH

Họ và tên:.....................

Lớp:...............

Tổ:...................

1. Tên bài thực hành:

Xác định suất điện động và điện trở trong của một pin điện hóa.

2. Bảng thực hành 12.1:

• Phương án thứ nhất:

a) Vẽ đồ thị U = f(I) trên giấy kẻ vuông (khổ A4) với tỉ xích thích hợp, hoặc vẽ trên máy vi tính, trong Microsoft Excel.

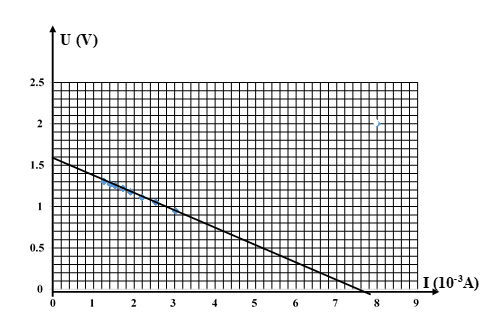
b) Nhận xét và kết luận:

• Dạng của đồ thị U = f(I) có dạng đường thẳng

• Hệ thức \[I = \frac{{\rm{E}}}{{{R_N} + r}}\] đối với đoạn mạch chứa nguồn điện có nghiệm đúng

c) Xác định tọa độ U0 và Im của các điểm tại đó đường kéo dài của đồ thị U = f(I) cắt trục tung và trục hoành:

• I = 0 ⇒ U0 = \[{\rm{E}}\] = 1,577 (V)

• \[U = 0 \Rightarrow {I_m} = \frac{{\rm{E}}}{{{R_0} + r}} = 0,075\,A\]

Từ đó suy ra: \[{\rm{E}}\] = 1,577 (V), r = 1,02 (\[\Omega \])

• Phương án thứ hai:

a) Tính các giá trị tương ứng của y và x trong bảng thực hành 12.1

b) Vẽ đồ thị y = f(x) trên giấy kẻ ô vuông (khổ A4) với tỉ xích thích hợp, hoặc vẽ trên máy vi tính, trong Microsoft Excel.

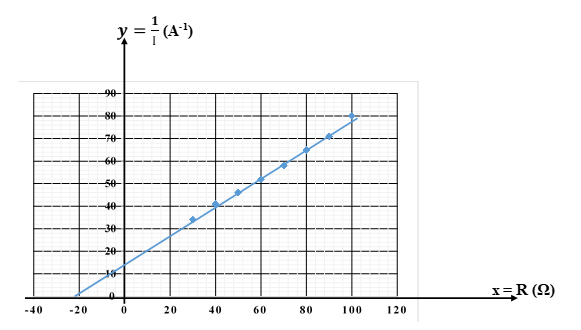
c) Nhận xét và kết luận:

• Dạng của đồ thị y = f(x) có giống với Hình 12,6

• Định luật Ôm đối với toàn mạch (Hệ thức 12.2) có được nghiệm đúng

d) Xác định tọa độ xm và y0 của các điểm đó đường kéo dài của đồ thị y = f(x) cắt trục tung và trục hoành:

• y = 0 ⇒ xm = -b = - (RA + R0 + r ) = -(20 + 1,98 + r) = -23 (\[\Omega \])

\[x = 0 \Rightarrow {y_0} = \frac{b}{{\rm{E}}} = \frac{{23}}{{\rm{E}}} = 14,48\]

Từ đó suy ra: \[{\rm{E}}\] = 1,577 (V), r = 1,02 (\[\Omega \])

Bài 5: Một bếp điện có ghi 220 V – 1000 W được sử dụng với hiệu điện thế 220V để đun sôi 2,5 lít nước ở nhiệt độ ban đầu 20°C thì mất một thời gian là 14 phút 35 giây.

1/ Tính hiệu suất của bếp. Biết nhiệt dung riêng của nước là 4200 J/kg.K

2/ Mỗi ngày đun sôi 5 lít nước ở điều kiện như trên thì trong 30 ngày sẽ phải trả bao nhiêu tiền điện cho việc đun nước này. Cho biết giá 1 kWh điện là 800 đồng.

Lời giải:

1. Nhiệt lượng cần cung cấp cho nước để nước sôi là:

\[{Q_{ci}} = mc.\left( {{t_2} - {t_1}} \right) = 2,5.4200.\left( {100 - 20} \right) = 840000\;\left( J \right)\]

\[t = 14\;ph\'u t\;35s = 875s\]

Nhiệt lượng bếp toả ra là: \[{Q_{tp}} = {\rm{P}}\,t = 1000.875 = 875000\;\left( J \right)\]

Hiệu suất của bếp là:

$H=\frac{Q_{ci}}{Q_{tp}}.100\%=\frac{840000}{875000}.100\%=96\%$

Vậy H = 96%

2. Đổi 1000 W = 1 kW

Thời gian để đun sôi 5 lít nước là: 875.2 = 1750s = \[\frac{{35}}{{72}}h\]

Số điện dùng trong 1 tháng là: 1.\[\frac{{35}}{{72}}\].30 = \[\frac{{175}}{{12}}\]kWh

Số tiền phải trả cho 1 tháng là: 800. \[\frac{{175}}{{12}}\] = 11667 đồng

Vậy 1 tháng phải trả 11667 đồng.

Bài 6: Một bếp điện có ghi 220 V – 1000 W được mắc vào mạng điện có hiệu điện thế 220 V để đun sôi 2 lít nước có nhiệt độ ban đầu là 200C. Biết hiệu suất của bếp là 80%, nhiệt lượng cung cấp để đun cho nước sôi được coi là có ích. Biết cnước = 4200 J/ kg.K. Nhiệt lượng do bếp tỏa ra và thời gian đun nước lần lượt là:

A. 787 500 J và 840 s.                                          

B. 840 000 J và 840 s.

C. 78 600 J và 5 600 s.                                

D. 756 500 J và 132 s.

Lời giải:

Đáp án: B

Nhiệt lượng cung cấp để đun sôi nước: \[{Q_{ci}} = m.c.{\rm{\Delta }}t = 2.4200.\left( {100 - 20} \right) = 672000\,\,J\]

Hiệu suất của bếp:\[H = \frac{{{Q_{ci}}}}{Q} \Rightarrow Q = \frac{{{Q_{ci}}}}{H}\]

Nhiệt lượng tỏa trên bếp: \[Q = \frac{{{Q_{ci}}}}{H} = \frac{{672000}}{{0,8}} = 840000\,\,J\]

Thời gian đun: \[t = \frac{A}{{\rm{P}}} = \frac{Q}{{\rm{P}}} = \frac{{840000}}{{1000}} = 840\,\,s\]

Bài 7: Một bóng đèn Đ loại 6 V – 3 W mắc nối tiếp với một biến trở vào nguồn điện có hiệu điện thế không đổi 9 V. Biết đèn sáng bình thường, công suất tiêu thụ trên biến trở là:

Lời giải:

Vì đèn sáng bình thường nên:

U = Uđm = 6 V

P = Pđm = 3 W

Cường độ dòng điện chạy qua đèn: I = P/U= 3/6 = 0,5 A

Vì Đ nối tiếp biến trở nên I = Ib = Iđ = 0,5 A

và U = Ub + Uđ => Ub = U - Uđ = 9 – 6 = 3 V

Vậy công suất tiêu thụ trên biến trở là: Pb = Ub . I = 3 . 0,5 = 1,5 W

Bài 8: Hai quả cầu nhỏ giống nhau, có cùng khối lượng 2,5 g, điện tích 5.10^-7​ C được treo tại cùng một điểm bằng hai sợi dây mảnh. Do lực đẩy tĩnh điện hai quả cầu tách ra xa nhau một đoạn 60 cm, lấy g = 10 m/s²​. Góc lệch của dây so với phương thẳng đứng là

A. 600​
B. 300​
C. 140​
D. 450​

Lời giải:

Đáp án: C

$\tan \alpha =\frac{F_d}{P}=\frac{k.\frac{q^2}{r^2}}{mg}=\frac{{9.10}^9.\frac{{\left({5.10}^{-7}\right)}^2}{0,6^2}}{2,{5.10}^{-3}.10}=0,25\Rightarrow \alpha \approx {14}^0$

Bài 9: Tính độ dài từ ga Hà Nội đến ga Thanh Hóa và đoạn đường sắt từ ga Thanh Hóa đến ga Vinh biết khoảng cách từ Hà Nội đến Vinh là 319 km và từ Hà Nội đến Thanh Hóa xa hơn từ Thanh Hóa đến Vinh là 31 km.

Lời giải:

Gọi x, y và z  lần lượt là quãng đường từ Hà Nội đến Vinh, Thanh Hóa đến Vinh và Hà Nội đến Thanh Hóa

Theo bài ra ta có:

y + z = x = 319 

z - y = 31

\[ \Rightarrow \] z = 175 và y = 144

Vậy quãng đường từ Thanh Hóa đến Vinh dài: 144 km

Hà Nội đến Thanh Hóa dài: 175 km

Bài 10: Hút bớt không khí trong vỏ hộp sữa bằng giấy, ta thấy vỏ hộp bị bẹp theo nhiều phía. Hãy giải thích tại sao.

Lời giải: Khi hút bớt không khí hộp sữa, khi đó áp suất trong hộp sữa nhỏ hơn áp suất khí quyển nên vỏ hộp sữa bị bẹp về nhiều phía.

Bài 11: Một cục nước đá được thả nổi trong một cốc đựng nước. Chứng minh rằng khi nước đá tan hết thì mực nước trong cốc không thay đổi.

Lời giải:

Gọi P₁ là trọng lượng của cục nước đá khi chưa tan.

\[{V_1}\] là thể tích của phần nước bị cục nước đá chiếm chỗ.

\[{d_n}\] là trọng lượng riêng của nước

\[{F_a}\] là lực đẩy Ác – si –mét tác dụng lên cục nước đá khi chưa tan.

Cục đá nổi trong nước nên \[{P_{da}} = {F_A} = {V_1}{d_n}\] \[ \Rightarrow {V_1} = \frac{{{P_{da}}}}{{{d_n}}}\,\,\,\left( 1 \right)\]

Gọi \[{V_2}\;\]là thể tích của nước do cục nước đá tan hết tạo thành, \[{P_2}\] là trọng lượng của lượng nước do đá tan ra, ta có: \[{V_2} = \frac{{{P_2}}}{{{d_n}}}\]

Vì khối lượng của cục nước đá và khối lượng của lượng nước do cục nước đá tan hết tạo thành phải bằng nhau, nên: \[{P_2} = {P_{da}}\] và \[{V_2} = \frac{{{P_2}}}{{{d_n}}}\]

Từ (1) và (2) \[ \Rightarrow {V_1} = {V_2}\]. Thể tích của phần nước đá chiếm chỗ đúng bằng thể tích của nước trong cốc nhận được khi nước đá tan hết. Do đó mực nước trong cốc không thay đổi.

Bài 12: Một cục nước đá đang nổi trong bình nước. Mực nước trong bình thay đổi như thế nào khi cục nước đá tan hết:

A. Tăng                                                      

B. Giảm

C. Không đổi                                                       

D. Không xác định được

Lời giải:

Đáp án: C

Gọi \[{P_d}\] là trọng lượng của cục đá khi chưa tan hết

\[{V_1}\] là thể tích của phần nước đá bị cục đá chiếm chỗ

\[{d_n}\] là trọng lượng riêng của nước

\[{F_A}\] là lực đẩy Ác-si-mét tác dụng lên nước đá khi chưa tan

\[{P_2}\] là trọng lượng của cục nước đá tan hết tạo thành

\[{V_2}\;\]là thể tích của nước do cục nước đá tan hết tạo thành

Ta có:

+ Khi cục nước đá đang nổi trong bình nước, thì trọng lượng và lực đẩy Ác-si-mét cân bằng với nhau: \[{P_d} = {F_A} = {V_1}.{d_n} \Rightarrow {V_1} = \frac{{{P_d}}}{{{d_n}}}\]

+ Trọng lượng của lượng nước do cục nước đá tan hết tạo thành là:

\[{P_2}\]=\[{V_2}\;\].\[{d_n}\]→\[{V_2}\;\]= \[\frac{{{P_2}}}{{{d_n}}}\]

Vì khối lượng của cục nước đá và khối lượng của lượng nước do cục nước đá tan hết tạo thành phải bằng nhau, nên: \[{P_2}\]= \[{P_d}\]→\[{V_2}\;\]= \[{V_1}\]

=> Thể tích của phần nước đá bị chiếm chỗ đúng bằng thể tích của nước trong cốc nhận được khi nước đá tan hết.

=> Mực nước trong cốc không thay đổi.

Bài 13: Một vật chuyển động thẳng đều theo trục Ox có phương trình tọa độ là: x = x_o + vt. Với x_o ≠ 0 và v ≠ 0. Điều khẳng định nào sau đây là đúng?

A. Tọa độ ban đầu của vật không trùng với gốc tọa độ.

B. Vật chuyển động ngược chiều dương của trục tọa độ.

C. Tọa độ của vật có giá trị không đổi theo thời gian.

D. Vật chuyển động theo chiều dương của trục tọa độ.

Lời giải:

A – đúng: vì xo ≠ 0 nên toạ độ ban đầu của vật không trùng gốc toạ độ

B. D – sai: vì đề bài chỉ cho v ≠ 0 chứ không cho v > 0 hay v < 0 nên không thể khẳng định được vật chuyển động theo chiều dương hay chiều âm.

C – sai: vì toạ độ thay đổi theo thời gian

Bài 14: Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là $x_1=4cos\left(10t+\frac{\pi }{4}\right),x_2=3cos\left(10t-\frac{3\pi }{4}\right)$. Độ lớn vận tốc của vật ở vị trí cân bằng là bao nhiêu?

Lời giải:

Biên độ dao động tổng hợp là: A = 1 cm

Độ lớn vận tốc của vật ở vị trí cân bằng: vmax = 1.10 = 10 cm/s

Bài 15: Con lắc lò xo treo thẳng đứng, vật ở vị trí cân bằng lò xo dãn 10 cm. Lấy $g=10\left(\frac{m}{s^2}\right)$. Từ vị trí cân bằng ta kích thích cho vật dao động điều hòa theo phương thẳng đứng. Tỉ số giữa thời gian lò xo nén và dãn trong một chu kì là \[\frac{1}{3}\]. Khi qua vị trí cân bằng vận tốc của vật có độ lớn là:

A. 80 cm/s.                              

B. 200 cm/s.

C. 100 cm/s.                  

D. \[100\sqrt 2 \] cm/s.

Lời giải:

Đáp án D.

Tỉ số giữa thời gian lò xo nén và dãn trong một chu kì là \[\frac{1}{3}\].

Suy ra thời gian lò xo bị nén trong 1 chu kì là 0,25T nên

\[{t_{nen}} = \frac{T}{\pi }\arccos \frac{{\Delta {\ell _0}}}{A} \Rightarrow \frac{T}{4} = \frac{T}{\pi }\arccos \frac{{\Delta {\ell _0}}}{A}\]\[ \Rightarrow \Delta {\ell _0} = A\frac{{\sqrt 2 }}{2} \to A = 10\sqrt 2 (cm)\]

\[{V_{\max }} = \omega A = \sqrt {\frac{g}{{\Delta \ell }}} .A = 100\sqrt 2 \](cm/s)

Bài 16: Kết luận sai về ảnh hưởng của vật lí đến một số lĩnh vực trong đời sống và kĩ thuật:

A. Vật lí đem lại cho con người những lợi ích tuyệt vời và không gây ra một ảnh hưởng xấu nào.

B. Vật lí ảnh hưởng mạnh mẽ và có tác động làm thay đổi mọi lĩnh vực hoạt động của con người.

C. Kiến thức vật lí trong các phân ngành được áp dụng kết hợp để tạo ra kết quả tối ưu.
D. Vật lí là cơ sở của khoa học tự nhiên và công nghệ.

Lời giải:

Đáp án A

Vì vật lí đem lại cho con người những lợi ích tuyệt vời bên cạnh đó nếu không biết cách phát triển, sử dụng vật lí vào cuộc sống đúng mục đích thì sẽ gây ra những hậu quả nghiêm trọng như phá huỷ môi trường, chiến tranh vũ khí hạt nhân…

Bài 17: Một thỏi đồng có khối lượng 176 g được kéo thành dây dẫn có tiết diện tròn, điện trở của dây dẫn bằng 32 Ω. Tính chiều dài và đường kính tiết diện của dây dẫn. Cho biết khối lượng riêng của đồng là \[8,{8.10^3}\;kg/{m^3}\] và điện trở suất của đồng bằng  \[1,{6.10^{ - 8}}\Omega m\]

A. \[\ell \] = 100 m; d = 0,72 mm.                                   

B. \[\ell \] = 200 m; d = 0,36 mm.

C. \[\ell \]= 200 m; d = 0,18 mm.

D. \[\ell \]= 250 m; d = 0,72 mm.

Lời giải:

Đáp án B

Khối lượng thỏi đồng: \[m = V.D = S.\ell .D \Rightarrow S = \frac{m}{{\ell .D}}\]

Điện trở trên dây dẫn: \[R = \rho \frac{\ell }{S} = \rho \frac{{{\ell ^2}.D}}{m}\]

$\to \mathcal{l}=\sqrt{\frac{m.R}{\rho .D}}=\sqrt{\frac{{176.10}^{-3}.32}{1,{6.10}^{-8}.8,{8.10}^3}}=200\left(m\right)$

Ta có: \[S = \rho \frac{\ell }{R} = \frac{{1,{{6.10}^{ - 8}}.200}}{{32}} = {10^{ - 7}}({m^2})\]

\[m = V.D = S.\ell .D = \frac{1}{4}\pi .{d^2}.\ell .D\]

$\to d=\sqrt{\frac{4S}{\pi }}=0,36mm$

Bài 18: Giữa hai đầu mạng điện có mắc song song 3 dây dẫn điện trở lần lượt là R₁ = 4 Ω, R₂ = 5 Ω, R₃ = 20 Ω. Tìm hiệu điện thế hai đầu đoạn mạch nếu cường độ dòng điện trong mạch chính là 2,2 A.

A. 8 V.       

B. 11 V.

C. 63,8 V.                                                  

D. 4,4 V.

Lời giải:

Ba điện trở mắc song song nên ta có: \({U_A}_B = 4{I_1} = 5{I_2} = 20{I_3}\) và \(I = {I_1} + {I_2} + {I_3}\).

Suy ra hệ 3 phương trình: \(\left\{ \begin{array}{l}4{I_1} - 5{I_2} = 0\\4{I_1} - 20{I_3} = 0\\{I_1} + {I_2} + {I_3} = 2,2\end{array} \right.\)\( \Rightarrow {I_1} = 1,1A;{I_2} = 0,88A;{I_3} = 0,22A\)

Hiệu điện thế giữa 2 đầu mạch là: \(U = {U_1} = {I_1}{R_1} = 1,1.4 = 4,4V\)

Bài 19: Giữa hai đầu mạch điện có mắc song song 3 dây dẫn điện trở lần lượt là R₁ = 4 Ω, R₂ = 5 Ω, R₃ = 20 Ω. Tính cường độ dòng điện qua R₁. Nếu cường độ dòng điện trong mạch chính là 5A.

Lời giải:

Ta có: \[{R_1}{\rm{// }}{R_2}{\rm{//}}\,{R_3}\]

Ta có:

Mà \[{R_1}{\rm{// }}{R_2}{\rm{//}}\,{R_3}\]\( \to {U_{AB}} = {U_1} = {U_2} = {U_3}\)\( \to {I_1} = \frac{{{U_{AB}}}}{{{R_1}}} = \frac{{10}}{4} = 2,5(A)\)

\({I_2} = \frac{{{U_{AB}}}}{{{R_2}}} = \frac{{10}}{5} = 2(A)\)

\({I_3} = \frac{{{U_{AB}}}}{{{R_3}}} = \frac{{10}}{{20}} = 0,5(A)\)

Bài 20: Từ độ cao h = 80 m, người ta ném một quả cầu theo phương nằm ngang với v₀ = 20 m/s. Xác định vị trí và vận tốc của quả cầu khi chạm đất. Cho rằng sức cản của không khí không đáng kể, g = 10 m/s²

Lời giải:

Vị trí rơi là tầm xa: $L=v_0.\sqrt{\frac{2.h}{g}}=80m$

Thời gian rơi: $t=\sqrt{\frac{2.h}{g}}=4s$

Vận tốc chạm đất: $v=\sqrt{{v_x}^2+{v_y}^2}=\sqrt{{v_0}^2+{\left(gt\right)}^2}=44,7m/s$

Bài 21: Thả rơi một vật từ độ cao 80 m xuống mặt đất lấy g = 10 m/s²

a) Xác định vận tốc khi chạm đất.

b) Xác định vị trí khi thế năng bằng 3 lần động năng.

c) Vận tốc của vật bằng bao nhiêu để động năng bằng thế năng.

Lời giải:

a. Thời gian chạm đất là:

$h=\frac{1}{2}g{t}^2\Rightarrow t=\sqrt{\frac{2.h}{g}}=\sqrt{\frac{2.80}{10}}=4s$

\[ \Rightarrow v = g.t = 10.4 = 40m/s\]

Vậy \[v = 40m/s\]

b. Tại độ cao 80 m thì: \[W = mgh = m.10.80 = 800.m\]

Tại độ cao h' thì: \[ \Rightarrow {W_t} = \frac{1}{4}W\]

$W_t=mg{h}^{\text{'}}=m\mathrm{.10.}{h}^{\text{'}}=10.m.h^{\text{'}}$

Theo định luật bảo toàn cơ năng có: $10.m.h^{\text{'}}=\frac{1}{4}\mathrm{.800.}m$

$\Rightarrow h^{\text{'}}=20\left(m\right)$

Vậy $h^{\text{'}}=20\left(m\right)$

c. Khi $W_t=W_{đ}\Rightarrow W=\frac{1}{2}W$ \[ \Leftrightarrow \frac{1}{2}m{v^{'2}} = \frac{1}{2}.800.m\] $\Rightarrow v^{\text{'}}=20\sqrt{2}m/s$

Vậy $v^{\text{'}}=20\sqrt{2}m/s$

Bài 22: Từ đỉnh mặt phẳng nghiêng có độ cao h = 2,5 m thả vật m = 400 g trượt không ma sát xuống chân mặt phẳng nghiêng, khi đến chân mặt phẳng nghiêng vật tiếp tục chuyển động vào một cung tròn có bán kính R = 1 m. Động năng của vật tại vị trí hợp với phương thẳng đứng góc 60° (hình vẽ).

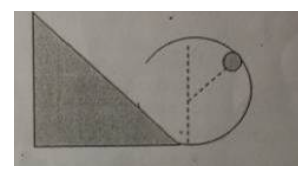
Lời giải

Chọn mốc tính thế năng tại chân mặt phẳng nghiêng.

Cơ năng tại vị trí đỉnh mặt phẳng nghiêng:

\[W = {W_d} + {W_t} = 0 + mgh = 0,4.10.2,5 = 10\,J\]

Tại vị trí hợp với phương thẳng đứng góc 60° thì độ cao của vật so với mặt phẳng ngang là: \[h' = R + R.\cos {60^0} = 1 + 1.\cos {60^0} = 1,5\,m\]

Cơ năng tại vị trí đang xét: \[W = {W_d} + {W_t} = {W_d} + 0,4.10.1,5 = {W_d} + 6\]

Theo định luật bảo toàn cơ năng: \[{W_d} = 10 - 6 = 4J\]

Bài 23: Một vật được ném theo phương ngang từ độ cao 80 m với vận tốc ban đầu 30 m/s lấy g = 10m/s².

a) Viết phương trình quỹ đạo của vật.

b) Tính thời gian kể từ lúc ném đến lúc vật chạm đất.

c) Tính tầm ném xa của vật.

Lời giải:

Chọn hệ quy chiếu gắn với mặt đất, chiều dương hướng lên, chọn mặt đất làm vật mốc

a. Ox: v_0x = v = 30 m/s; a_x = 0

Oy: v_0y = 0; a_y = -g = -10 m/s²

Ta có: x = v_0x.t = 30t ⇔ \[t = \frac{x}{{30}}\]

\[y = {y_0} + \frac{1}{2}a{t^2}\]= \[80 - \frac{1}{2}.10.\frac{{{x^2}}}{{{{30}^2}}}\]\[ \Leftrightarrow y = 80 - \frac{1}{{180}}{x^2}\]

b. Có: \[y = 80 - \frac{1}{2}.10.{t^2}\], thay y = 0 ta được: t = 4 (s)

Vậy thời gian kể từ lúc ném đến lúc chạm đất là 4 (s)

c. Tầm xa của vật là: L = x = v_0X.t = 30.4 = 120 (m)

Bài 24: Một vật có khối lượng 7,5 kg buộc vào một sợi dây. Cần phải giữ dây một lực bằng bao nhiêu để vật cân bằng?

Lời giải:

Lực hút Trái đất tác dụng lên vật là: 7,5 . 10 = 75 N

Mà vật được buộc vào dây để cố định cho vật cân bằng thì lực căng của dây phải bằng trọng lượng của vật tức 75 N

Vậy cần phải giữ dây một lực 75N để vật cân bằng.

Bài 25: Một ôtô tải đang chuyển động với vận tốc 72 km/h trên mặt đường với ngang hệ số ma sát 0,2 thì tắt máy. Dùng độ biến thiên động năng tìm quãng đường mà ôtô đi được kể từ khi tắt máy cho đến khi dừng lại. Lấy g = 10 m/ \({s^2}\).

Lời giải:

72 km/h = 20 m/s. Khi dừng lại v₂ = 0

Áp dụng độ biến thiên động năng:

$\begin{array}{l} \frac{m{v}_2^2}{2}-\frac{m{v}_1^2}{2} = -\mu mgS\\ \iff 0-\frac{{20}^2}{2}=-0,\mathrm{2.10.}S\end{array}$

 => S =100 m.

Vậy quãng đường mà oto đi được kể từ khi tắt máy đến khi dừng lại là: S = 100 m.

Bài 26: Chuyển động thẳng đều là:

A. Chuyển động thẳng, trong đó chất điểm có gia tốc không đổi.

B. Chuyển động có quỹ đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.

C. Chuyển động có quỹ đạo là đường thẳng và gia tốc như nhau trên mọi quãng đường.

D. Chuyển động thẳng, trong đó chất điểm có vẫn tốc tức thời thay đổi.

Lời giải:

Đáp án B

Chuyển động thẳng đều là: Chuyển động có quỹ đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.

Bài 27: Một con lắc lò xo treo thẳng đứng gồm vật có khối lượng 250 g và một lò xo nhẹ có độ cứng 100 N/m. Kích thích cho vật dao động điều hòa theo phương thẳng đứng với biên độ 5 cm. Tính thời gian lò xo bị giãn trong một chu kì.

A. π/30 (s).

B. π/15 (s).

C. π/10 (s).

D. π/5 (s).

Lời giải:

Đáp án B

\(\Delta l = \frac{{mg}}{k} = 2,5cm\)

\(\Delta l = \frac{A}{2}\)

Nên thời gian lò xo giãn trong 1 chu kì là: \(\frac{{2T}}{3} = \frac{\pi }{{15}}s\)

Bài 28: Trên vỏ một tụ điện có ghi 20 μF – 200 V. Nối hai bản của tụ điện với một hiệu điện thế 120 V.

a) Tính điện tích của tụ điện.

b) Tính điện tích tối đa mà tụ điện tích được.

Lời giải:

a. Trên vỏ một tụ điện có ghi 20 μF – 200 V

\( \to C = 20{\rm{ }}\mu F = {20.10^{ - 6}}\;F,{\rm{ }}{U_{max}} = 200V\)

Khi nối hai bản của tụ điện với hiệu điện thế 120 V thì tụ sẽ tích điện là:

\(Q = C.U = {20.10^{ - 6}}.120 = {2400.10^{ - 6\;}}C = 2400{\rm{ }}\mu C\)

b. Điện tích tối đa mà tụ tích được (khi nối hai đầu tụ vào hiệu điện thế 200 V):

\({Q_{max}}\; = C.{U_{max}}\; = {20.10^{ - 6}}.200 = {4.10^{ - 3\;}}C = 4000{\rm{ }}\mu C\)

Bài 29: Cho 2 điểm AB cùng nằm trên 1 đường sức điện trường do một điện tích điểm Q > 0  đặt tại O gây ra, biết độ lớn cường độ điện trường tại A là 36 V/m tại B là 9 V/m.

a. Xác định cường độ điện trường tại trung điểm M của AB.

b. Nếu đặt tại M một điện tích điểm Qo = -10^-2 C thì độ lớn của lực điện tác dụng lên Qo là bao nhiêu. Xác định phương và chiều của lực.

Lời giải:

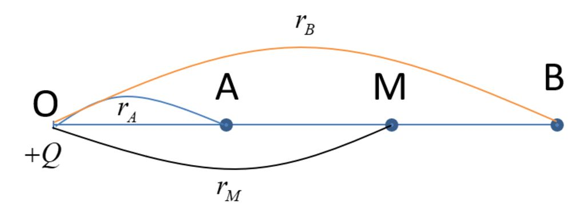
a. Ta có: \[\left\{ \begin{array}{l}{E_A} = k\frac{Q}{{r_A^2}} = k\frac{Q}{{O{A^2}}}\\{E_B} = k\frac{Q}{{r_B^2}} = k\frac{Q}{{O{B^2}}}\end{array} \right.\]\[ \Rightarrow \frac{{{E_A}}}{{{E_B}}} = \frac{{O{B^2}}}{{O{A^2}}} = \frac{{36}}{9} = 4\]\[ \Rightarrow OB = 2OA\]

Lại có: \[OM = \frac{{OA + OB}}{2} \Rightarrow OM = \frac{{3OA}}{2}\]

Cường độ điện trường tại M: \[{E_M} = k\frac{Q}{{O{M^2}}} = k\frac{Q}{{\frac{9}{4}O{A^2}}} = \frac{4}{9}{E_A} = 16V/m\]

b. Ta có: $\overrightarrow{F}=Q_0\overrightarrow{E}$

Do \[{Q_0} < 0 \Rightarrow \]Lực điện tại M khi đặt điện tích \[{Q_0}\]:

+ Có phương trùng phương của \[\overrightarrow {{E_M}} \]

+ Có chiều ngược chiều của \[\overrightarrow {{E_M}} \]

+ Có độ lớn: \[F = \left| {{Q_0}} \right|{E_M} = {10^{ - 2}}.16 = 0,16\,\,N\]

Bài 30: Cho hai điểm A  và B cùng nằm trên một đường sức điện do điện tích q > 0 gây ra. Biết độ lớn của cường độ điện trường tại A là 36 V/m, tại B là 9 V/m. Xác định cường độ điện trường tại trung điểm M của AB.

A. 10 V/m.

B. 15 V/m.

C. 20 V/m.

D. 16 V/m.

Lời giải:

$E~\frac{1}{r^2}\to \frac{r_B}{r_A}=\sqrt{\frac{E_A}{E_B}}=\sqrt{\frac{36}{9}}=2$

Ta chuẩn hóa \({r_A} = 1 \to {r_B} = 2\)

Với M là trung điểm của AB

\( \to {r_M} = {r_A} + \frac{{{r_B} - {r_A}}}{2} = 1 + \frac{{2 - 1}}{2} = 1,5\)\( \to {E_M} = {\left( {\frac{{{r_A}}}{{{r_M}}}} \right)^2}{E_A} = {\left( {\frac{1}{{1,5}}} \right)^2}36\)= 16 V/m.

Đáp án B

Bài 31: Một quả cầu khối lượng 4,5.10-3 kg treo vào một sợi dây dài 1 m. Quả cầu nằm giữa hai tấm kim loại song song, thẳng đứng như hình vẽ. Hai tấm cách nhau 4 cm. Đặt một hiệu điện thế 750 V vào hai tấm đó thì quả cầu lệch ra khỏi vị trí ban đầu 1 cm. Tính điện tích của quả cầu. Lấy g = 10 m/s²

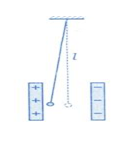
A. q = \[2,{4.10^{ - 8}}\;\]C.

B. q = -\[2,{4.10^{ - 8}}\;\]C.

C. q = -\[4,{8.10^{ - 8}}\;\]C.

D. q = \[4,{8.10^{ - 8}}\;\]C.

Lời giải:

Đáp án B

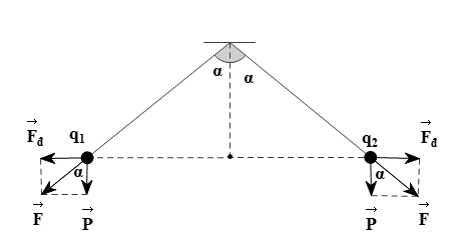
Hai tấm cách nhau: d = 4 cm. Quả cầu lệch khỏi vị trí ban đầu: a = 1 cm. Chiều dài của sợi dây: $\mathcal{l}=1m$

Quả cầu chịu sự tác dụng của các lực như hình vẽ:

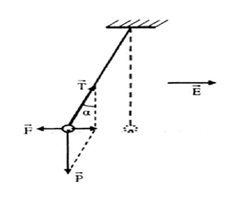
Điều kiện cân bằng của quả cầu: $\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{T}=\overrightarrow{0}$

Ta thấy \[\overrightarrow F \] ngược chiều với \[\overrightarrow E \] nên quả cầu có điện tích âm (q < 0)

Lực điện tác dụng lên quả cầu có độ lớn: \[F = \left| q \right|E = \frac{{\left| q \right|U}}{d}\]

Dựa trên hình vẽ ta có:

$\begin{array}{l}tan\alpha =\frac{F}{P}=\frac{a}{\mathcal{l}}\\ \iff \frac{\left|q\right|U}{d.m.g}=\frac{a}{\mathcal{l}}\\ \Rightarrow \left|q\right|=\frac{d.m.g.a}{U.\mathcal{l}}=\frac{{4.10}^{-2}.4,{5.10}^{-3}{\mathrm{.10.1.10}}^{-2}}{750.1}=2,{4.10}^{-8}\end{array}$

Do $q<0\to q=-2,{{4.10}^{-}}^8 C$.

Bài 32: Nêu ý nghĩa hằng số điện môi

Lời giải:

Hằng số điện môi có ý nghĩa rất quan trọng trong lĩnh vực điện cơ khí. 

Bài 33: Từ vách đá, một người thả rơi một hòn đá xuống vực sâu. Từ lúc buông cho đến lúc nghe thấy tiếng chạm của hòn đá mất 6,5 (s). Biết rằng vận tốc truyền âm trong không khí xem như không đổi và bằng 360 m/s. Hãy tính:

a) Thời gian hòn đá rơi?

b) Độ cao từ vách núi xuống đáy vực?

Lời giải:

Chọn gốc tọa độ tại vị trí vật rơi, gốc thời gian lúc vật bắt đầu rơi, chiều dương từ trên xuống.

Thời gian rơi đến khi nghe tiếng âm vọng lại là: \[t = {t_1} + {t_2} = 6,5\,\,s{\rm{ }}\left( 1 \right)\]

Thời gian rơi của đá là: \[{t_1} = \sqrt {\frac{{2s}}{g}} \,\, = \sqrt {\frac{{2s}}{{10}}} \,(2)\]

Thời gian âm vọng lại là: \[{t_2} = \frac{s}{{360}}\,\,\,(3)\]

Từ (1), (2), (3) ⇒ s = 180 m

Vậy h = s = 180 m. Thời gian rơi của vật là t = 6 s.

Bài 34: Từ công thức vận tốc v = v₀+ a.t. Hãy suy ra công thức tính t, v₀ ?

Lời giải:

Từ công thức vận tốc v =\({v_0}\)+ a.t, suy ra công thức tính t, \({v_0}\)

\[t = \frac{{(v - {v_0})}}{a}\]

\({v_0}\) = v - at

Bài 35: Trong công thức tính vận tốc của chuyển động thẳng nhanh dần đều v = v₀ + at thì:

A. v luôn luôn dương.

B. a luôn luôn dương.

C. a luôn luôn cùng dấu với v.

D. a luôn luôn ngược dấu với v.

Chọn đáp án đúng.

Lời giải:

Đáp án C.

Trong chuyển động thẳng nhanh dần đều thì a.v > 0. Tức là a và v luôn cùng dấu.

Bài 36: Cho F₁ = 30N, F = 50N như hình vẽ. Lực F₂ có giá trị như thế nào?

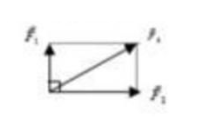
Lực \({F_2}\) là: $F_2=\sqrt{F^2-{F_1}^2}=\sqrt{{50}^2-{30}^2}=40N$

Vậy \({F_2}\)= 40 N.

Bài 37: Có một vật làm bằng kim loại, khi treo vật đó vào một lực kế và nhúng chìm trong một bình tràn đựng nước thì lực kế chỉ 8,5 N đồng thời lượng nước tràn ra có thể tích 0,5 lít. Hỏi vật đó có khối lượng là bao nhiêu và làm bằng chất gì? Cho khối lượng riêng của nước là 1000 kg/m³.

A. 13,5 kg – Nhôm.

B. 13,5 kg – Đá hoa cương.

C. 1,35 kg – Nhôm.

D. 1,35 kg – Đá hoa cương.

Lời giải:

Đáp án C

Ta có thể tích nước tràn ra ngoài đúng bằng thể tích vật chiếm chỗ và bằng: 

$V=0,5\mathcal{l}=0,5d{m}^3={5.10}^{-4}{m}^3$

Vật chịu tác dụng của trọng lực hướng xuống và lực đẩy Archimedes hướng lên.

Chọn trục toạ độ có phương thẳng đứng, chiều từ trên xuống dưới.

Lực đẩy Archimedes  tác dụng lên vật là: \[{F_A} = {\rho _n}Vg = {1000.5.10^{ - 4}}.10 = 5\,N\]

Trọng lượng của vật: \[P = F + {F_A} = 8,5 + 5 = 13,5N\]

Khối lượng của vật là: \[m = \frac{P}{{10}} = 1,35\,\,kg\]

Khối lượng riêng của vật: $\rho =\frac{m}{V}=\frac{1,35}{{5.10}^{-4}}=2700(kg/m^3)$

Vật đó là nhôm.

Bài 38: Lực F₁ tác dụng lên vật có khối lượng m₁ làm cho vật chuyển động với gia tốc a₁. Lực F₂ tác dụng lên vật có khối lượng m₂ làm cho vật chuyển động với gia tốc a₂. Biết \[{F_2} = \frac{{{F_1}}}{3}\] và \[{m_1} = \frac{{2{m_2}}}{5}\] thì \[\frac{{{a_2}}}{{{a_{^1}}}}\] bằng.

A. \[\frac{2}{{15}}\].

B. \[\frac{6}{5}\].

C. \[\frac{{11}}{5}\].

D. \[\frac{5}{6}\].

Lời giải:

Đáp án A

Theo đề ra \[{F_2} = \frac{{{F_1}}}{3} \Rightarrow \frac{{{F_2}}}{{{F_1}}} = \frac{1}{3}\]; \[{m_1} = \frac{{2{m_2}}}{5} \Rightarrow \frac{{{m_1}}}{{{m_2}}} = \frac{2}{5}\]

Ta có: \[{a_1} = \frac{{{F_1}}}{{{m_1}}};\,{a_2} = \frac{{{F_2}}}{{{m_2}}} \Rightarrow \frac{{{a_2}}}{{{a_1}}} = \frac{{\frac{{{F_2}}}{{{m_2}}}}}{{\frac{{{F_1}}}{{{m_1}}}}} = \frac{{{F_2}}}{{{F_1}}}.\frac{{{m_1}}}{{{m_2}}} = \frac{1}{3}.\frac{2}{5} = \frac{2}{{15}}\]

Bài 39: Lực F₁ tác dụng lên vật khối lượng m₁ làm vật chuyển động với gia tốc a₁. Lực F₂ tác dụng lên vật khối lượng m₂ (với \[{m_2}\] = \[{m_1}\]) làm vật chuyển động với gia tốc \[{a_2}\]. Nếu \[\frac{{{F_2}}}{{{F_1}}} = \frac{3}{2}\] thì tỉ số \[\frac{{{a_2}}}{{{a_1}}}\].

A. 3.

B. \[\frac{2}{3}\].

C. \[\frac{3}{2}\].

D. \[\frac{1}{3}\].

Lời giải:

Đáp án C

Ta có: \[\frac{{{a_2}}}{{{a_1}}} = \frac{{\frac{{{F_2}}}{{{m_2}}}}}{{\frac{{{F_1}}}{{{m_1}}}}} = \frac{{{F_2}}}{{{F_1}}}.\frac{{{m_1}}}{{{m_2}}} = \frac{3}{2}\] (do m1 = m2)

Bài 40: Trên một nồi cơm điện có ghi 220 V – 528 W

a) Tính cường độ định mức của dòng điện chạy qua dây nung của nồi.

b) Tính điện trở dây nung của nồi khi nồi đang hoạt động bình thường.

Lời giải:

a) Cường độ định mức của dòng điện chạy qua dây nung của nồi là:

Ta có: P  = UI ⇒ I = P  : U = 528 : 220 = 2,4A

b) Điện trở của dây nung khi nồi đang hoạt động bình thường là:

R = U : I = 220 : 2,4 = 91,7 Ω

Bài 41: Một con lắc đơn có chiều dài $\mathcal{l}=1m$, đầu trên treo vào trần nhà, đầu dưới gắn với vật có khối lượng m = 0,1 kg. Kéo vật ra khỏi vị trí cân bằng một góc α = 45° và buông tay không vận tốc đầu cho vật dao động. Biết \[g = 10m/{s^{_2}}\]. Hãy xác định cơ năng của vật?

A. 0,293 J.

B. 0,3 J.

C. 0,319 J.

D. 0,5 J.

Lời giải:

Đáp án A

Ta có: \[{\rm{W}} = {{\rm{W}}_{t\max }} = mg\ell (1 - \cos {\alpha _0})\]\[ = 0,1.10.1.(1 - \cos {45^0}) = 0,293J\]

Bài 42: Một con lắc đơn có chiều dài $\mathcal{l}=1m$, đầu trên treo vào trần nhà, đầu dưới gắn với vật có khối lượng m = 0,1 kg. Kéo vật ra khỏi vị trí cân bằng một góc α = 45° và buông tay không vận tốc đầu cho vật dao động. Biết \[g = 10m/{s^{_2}}\]. Hãy xác định động năng của vật khi vật qua vị trí có α = 30°

Lời giải:

Ta có: 

$\begin{array}{l}{W}_d=W-W_t\\ =mg\mathcal{l}(1-\cos {\alpha }_0)-mg\mathcal{l}(1-\cos \alpha )\\ =mg\mathcal{l}(\cos \alpha -\cos {\alpha }_0)\end{array}$

\[ = 0,1.10.1.(\cos {30^0} - \cos {45^0}) = 0,159J\]

Bài 43: Nêu một số ảnh hưởng của vật lí đến một số lĩnh vực trong đời sống và kĩ thuật.

A. Thông tin liên lạc.

B. Y tế.

C. Công nghiệp.

D. Cả A, B và C.

Lời giải:

Đáp án: D.

Vật lí ảnh hưởng rất nhiều đến các lĩnh vực trong đời sống và kĩ thuật như:

- Thông tin liên lạc

- Y tế

- Công nghiệp

- Giao thông vận tải

- Nông nghiệp

- Nghiên cứu khoa học

Bài 44: Khi nào vật có khả năng thực hiện công ? Cho ví dụ

Lời giải:

Khi có lực tác dụng vào vật làm vật chuyển dời theo phương không vuông góc với phương của lực thì có công cơ học.

Ví dụ:

- Người đẩy thanh lau nhà.

- Một người đi xe đạp cho xe tự đi từ đỉnh dốc xuống chân dốc.

- Quả mít rơi từ trên xuống.

Bài 45: Khi nào 1 vật thực hiện  công cơ học? công thức tính công cơ học? công suất là gì? Ý nghĩa công suất? công thức tính công suất?

Lời giải:

Khi có lực tác dụng vào vật làm vật chuyển dời theo phương không vuông góc với phương của lực thì có công cơ học

+ Công thức tính công cơ học: \[A = F.s.\cos \alpha \]

+ Đơn vị của công là Jun, (kí hiệu là J). 1 J = 1 N.1 m = 1 Nm.

+ Công suất là đại lượng đặc trưng có khả năng thực hiện công.

+ Công thức tính công suất: \[{\rm{P}} = \frac{A}{t}\]

Bài 46: Một vật khối lượng riêng 400 kg/m³ thả trong cốc nước có khối lượng riêng 1000 kg/m³. Hỏi vật chìm bao nhiêu phần trăm thể tích của nó trong nước?

A. 30%.

B. 40%.

C. 35%.

D. 45%.

Lời giải:

Đáp án B

Gọi V, V’ lần lượt là thể tích của vật và thể tích phần chìm trong nước của vật

D, D’ lần lượt là khối lượng riêng của vật và của nước

+ Trọng lượng của vật là: \(P = 10DV\)

+ Lực đẩy Ác-si-mét: \({F_A} = 10D'V'\)

Khi vật cân bằng trong nước, ta có: $P=F_A\leftrightarrow 10DV=10D\text{'}V\text{'}$

\( \to \frac{{V'}}{V} = \frac{D}{{D'}} = \frac{{400}}{{1000}} = 0,4\)

\( \Rightarrow \)Tỉ lệ phần trăm thể tích của vật chìm trong nước là 40%.

Bài 47: Một con lắc đơn có chiều dài $\mathcal{l}=2,45m$ dao động ở nơi có g = 9,8 m/s². Kéo con lắc lệch cung độ dài 5 cm rồi thả nhẹ cho dao động. Chọn gốc thời gian vật bắt đầu dao dộng. Chiều dương hướng từ vị trí cân bằng đến vị trí có góc lệch ban đầu. Phương trình dao động của con lắc là

A. \[s = 5\cos \left( {25 + \frac{\pi }{2}} \right)cm\]

B. \[s = 5\cos \left( {\frac{t}{2} + \frac{\pi }{2}} \right)cm\]

C. \[s = 5\cos \left( {2t} \right)cm\]

D. \[s = 5\cos \left( {\frac{t}{2} - \frac{\pi }{2}} \right)cm\]

Lời giải:

Đáp án C

Tần số góc của dao động: $\omega =\sqrt{\frac{g}{\mathcal{l}}}=2$ rad/s

Chiều dương hướng từ vị trí cân bằng đến vị trí góc lệch ban đầu, gốc thời gian lúc vật bắt đầu chuyển động → vật xuất phát từ biên dương → \[s = 5\cos \left( {2t} \right)cm\]

Bài 48: Một con lắc lò xo dao động điều hòa. Lò xo có độ cứng k = 40 N/m. Khi vật m của con lắc đang qua vị trí có li độ x = - 2 cm thì thế năng của con lắc là bao nhiêu?

A. - 0,016 J.

B. - 0,008 J.

C. 0,016 J.

D. 0,008 J.

Lời giải:

Đáp án D.

Thế năng của con lắc lò xo tại li độ x (m) được tính theo công thức: \[{{\rm{W}}_t} = \frac{1}{2}.k.{x^2}\]

Tại x = - 2 (cm) = 2.\[{10^{ - 2}}\] (m), thế năng của con lắc là: \[{{\rm{W}}_t} = \frac{1}{2}.k.{x^2} = 0,008(J)\]

Bài 49: Một con lắc lò xo được đặt nằm ngang gồm lò xo có độ cứng k = 40 N/m và vật nặng khối lượng m = 400 g. Từ vị trí cân bằng kéo vật ra một đoạn 8 cm rồi thả nhẹ cho vật dao động điều hòa. Sau khi thả vật \(\frac{{7\pi }}{{30}}\)s thì giữ đột ngột điểm chính giữa lò xo khi đó. Biên độ dao động của vật sau khi giữ lò xo là

A. \(4\sqrt 2 \) cm.

B. \(2\sqrt {14} \)cm.

C. \(2\sqrt 6 \) cm.

D. \(2\sqrt 7 \) cm.

Lời giải:

Đáp án D

Ta có: $T=2\pi \sqrt{\frac{m}{k}}=2\pi \sqrt{\frac{0,4}{40}}=\frac{\pi }{5}$ \[ \Rightarrow \frac{{7\pi }}{{30}} = \frac{{7T}}{6}\]

Tại thời điểm ban đầu vật xuất phát từ biên dương. Sau khoảng thời gian \[\frac{{7T}}{6}\] lúc đó vật đang ở vị trí 4 cm và tiến về VTCB.

Lúc giữ vật lại thì chỉ còn một nửa lò xo trong quá trình dao động

Lúc này \[k' = 2k\] và lò xo mới giãn 2 cm

\[A{'^2} = x{'^2} + \frac{{{v^2}}}{{\omega {'^2}}} = x{'^2} + (A{'^2} - {x^2}).\frac{{{\omega ^2}}}{{\omega {'^2}}} = x{'^2} + \left( {{A^2} - {x^2}} \right).\frac{k}{{k'}}\]

\[A' = 2\sqrt 7 \]

Bài 50: Mạch xoay chiều mắc nối tiếp gồm tụ điện có điện dung 19,6 (mF), điện trở thuần 100 (W), cuộn dây thuần cảm có độ tự cảm 159 (mH). Tần số dòng điện là 60 (Hz). Tổng trở của mạch điện là

A. \[150\,\Omega .\]

B. \[125\,\Omega .\]

C. \[4866\,\Omega .\]

D. \[140\,\Omega .\]

Lời giải:

Đáp án B

Cảm kháng: \[{Z_L} = 2\pi fL = 2\pi {.60.159.10^{ - 3}} \approx 60\,\Omega \]

Dung kháng: \[{Z_C} = \frac{1}{{2\pi fC}} = \frac{1}{{2\pi .60.19,{{6.10}^{ - 6}}}} \approx 135\,\Omega \]

Tổng trở: $Z=\sqrt{R^2+{\left(Z_L-Z_C\right)}^2}=125\Omega$

Bài 51: Vì sao người ta lại đặt tên cho các từ của nam châm là cực bắc và cực nam.

Lời giải:

Vì: Các đường sức từ của một nam châm được coi là theo quy ước xuất hiện từ cực bắc của nam châm và nhập lại ở cực nam.

Bài 52: Xác định cường độ dòng điện qua ampe kế theo mạch như hình vẽ. Biết \[{R_A} \approx 0;{R_1} = {R_3} = 30\Omega ;{R_2} = 5\Omega ,{R_4} = 15\Omega \] và \[U = 90V\]

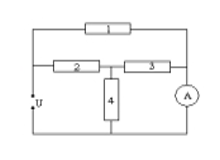
A. 4 A.

B. 9 A.

C. 5 A.

D. 2 A.

Lời giải:

Đáp án C

Mạch tương đương với mạch: 

Bài 53: Một vật sáng AB đặt vuông góc với trục chính của thấu kính cho ảnh thật. Nếu cho vật dịch chuyển lại gần thấu kính 30 cm thì ảnh sau của AB vẫn là ảnh thật nằm cách vật một khoảng như cũ và cao gấp 4 lần ảnh trước. Tiêu cự của thấu kính này là?

A. 10 cm.

B. 15 cm.

C. 20 cm.

D. 25 cm.

Lời giải:

Đáp án C

Vì trước và sau khi dịch chuyển vật ảnh vẫn luôn là ảnh thật nên ta có:

$\frac{A_2{B}_2}{A_1{B}_1}=\left(-\frac{A_2{B}_2}{AB}\right).\left(-\frac{AB}{A_1{B}_1}\right)=\frac{k_2}{k_1}=4$   (1)

Theo công thức thấu kính và công thức số phóng đại của ảnh ta được:

\(d' = f\left( {1 - k} \right);d = f\left( {1 - \frac{1}{k}} \right)\)

Độ dịch chuyển vật: $\Delta d=d_2-d_1=f.\left(\frac{1}{k_1}-\frac{1}{k_2}\right)=-30$ (do vật lại gần thấu kính).

Sau khi di chuyển vật lại gần, ảnh cách vật một khoảng như cũ nên ảnh di chuyển ra xa thêm đoạn 30 cm.

Độ dịch chuyển ảnh: \(\Delta d' = d{'_2} - d{'_1} = f.\left( {{k_1} - {k_2}} \right) = 30\)

Tỉ lệ độ dịch chuyển vật và độ dịch chuyển ảnh:

$\frac{\Delta d}{\Delta d\text{'}}=\frac{\frac{1}{k_1}-\frac{1}{k_2}}{k_1-k_2}=\frac{-1}{k_1.k_2}=\frac{30}{-30}=-1$

\( \Rightarrow {k_1}.{k_2} = 1\)   (2)

Ảnh thật nên \({k_1}\)< 0, \({k_2}\)< 0, từ (1) và (2)

$\Rightarrow k_1=-\frac{1}{2}$ và $k_2=-2\Rightarrow f=20cm$

Bài 54: Một vật sáng AB đặt thẳng góc với trục chính của một thấu kính cho ảnh thật. Nếu cho vật dịch lại gần thấu kính một khoảng 30 cm thì ảnh của AB vẫn là ảnh thật nằm cách vật một khoảng như cũ và lớn hơn gấp 4 lần.

a) Hãy xác định tiêu cự của thấu kính và vị trí ban đầu của vật AB.

b) Để có được ảnh cho bằng vật, phải dịch chuyển vật từ vị trí ban đầu đi một khoảng bằng bao nhiêu, theo chiều nào?

Lời giải:

Ta có công thức tính khoảng cách giữa ảnh và vật: \[L = \left| {d + d'} \right|\] mà trong cả hai trường hợp, ảnh là ảnh thật nên L = d + d'. Mặt khác, L không thay đổi nên trong hai trường hợp, d và d' đổi chỗ cho nhau: 

- Ban đầu: d1 = d thì d1' = d' 

- Sau đó: d2 = d' thì d2' = d 

- Theo bài ra: d1 - d2 = d - d' = 30 cm (1) 

- Thêm vào đó: chiều cao của vật là h, chiều cao của ảnh đầu là h1, chiều cao của ảnh sau là h2. 

Ta có: \[\frac{{{h_1}}}{h} = \frac{{{d_1}'}}{{{d_1}}} = \frac{{d'}}{d};\frac{{{h_2}}}{h} = \frac{{{d_2}'}}{{{d_2}}} = \frac{d}{{d'}}\] do đó: \[\frac{{{h_2}}}{{{h_1}}} = {\left( {\frac{d}{{d'}}} \right)^2} = 4\]

nên có \[\frac{d}{{d'}} = 2 \Rightarrow d = 2d'\,\,\,\left( 2 \right)\]

Từ (1) và (2) ta có d' = 30 cm, d = 60 cm => f = 20 cm 

b) Để ảnh cao bằng vật \[d = d' \Rightarrow \frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} = \frac{2}{d} \Rightarrow d = 2f = 40\,cm\] vậy phải dịch lại gần thấu kính 20 cm.

Bài 55: Tên đồng hồ đo điện là:

A. Ampe kế.

B. Vôn kế.

C. Ôm kế.

D. Cả 3 đáp án trên.

Lời giải:

Đáp án: D

Bài 56: Cho mạch điện như hình vẽ, nguồn điện có suất điện động E = 6,6 V điện trở trong r = 0,12 Ω, bóng đèn Đ1 (6 V – 3 W) và Đ2 (2,5 V – 1,25 W)

a) Điều chỉnh R1 và R2 sao cho 2 đèn sáng bình thường. Tính các giá trị của R1 và R2.

b) Giữ nguyên giá trị của R1, điều chỉnh biến trở R2 sao cho nó có giá trị R′2 = 1 Ω. Khi đó độ sáng của các bóng đèn thay đổi thế nào so với câu a?

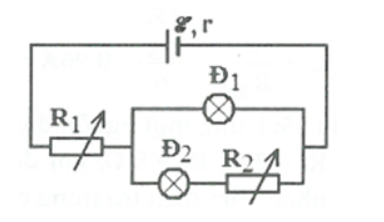
Lời giải:

Cường độ dòng điện định mức và điện trở của các đèn:

\({I_{d1}} = \frac{{{P_{d1}}}}{{{U_{d1}}}} = \frac{3}{6} = 0,5A;\)

\({I_{d2}} = \frac{{{P_{d2}}}}{{{U_{d2}}}} = \frac{{1,25}}{{2,5}} = 0,5A\)

\({R_{d1}} = \frac{{{U^2}_{d1}}}{{{P_{d1}}}} = \frac{{{6^2}}}{3} = 12\Omega \)

\({R_{d2}} = \frac{{{U^2}_{d2}}}{{{P_{d2}}}} = \frac{{2,{5^2}}}{{1,25}} = 5\Omega \)

Đèn sáng bình thường nên cường độ dòng điện qua mạch chính: \[I = {I_{d1}} + {I_{d2}} = 1A\]

Hiệu điện thế 2 đầu \[{R_2}\] bằng:\[{U_2} = {U_{d1}} - {U_{d2}} = 6 = 2,5 = 1,5V\]

Vậy điện trở: \[{R_2} = \frac{{{U_2}}}{{{I_{d2}}}} = \frac{{1,5}}{{0,5}} = 3\Omega ;\]

Hiệu điện thế hai đầu \[{R_1}\] bằng:

\[{U_1} = U - {U_{d1}} = (E - I.r) - {U_{d1}}\]\[ = (6,6 - 1.0,12) - 6 = 0,48V\]

Vậy điện trở: \[{R_1} = \frac{{{U_1}}}{I} = \frac{{0,48}}{1} = 0,48\Omega \]

b, Giữ nguyên giá trị của \[{R_1}\], điều chỉnh biến trở \[{R_2}\]sao cho nó có giá trị \[R{'_2} = 1\Omega \]

Khi đó mạch ngoài gồm \[{R_1}\]nt [ ]

\[{R_{d2 - 2}} = R{'_2} + {R_{d2}} = 1 + 5 = 6\,\Omega \]

\[{R_{d1 - d2 - 2}} = \frac{{{R_{d1}}.{R_{d2 - 2}}}}{{{R_{d1}} + {R_{d2 - 2}}}} = \frac{{12.6}}{{12 + 6}} = 4\Omega \]

Điện trở tương đương ở mạch ngoài: \[{R_{td}} = {R_1} + {R_{d1 - d2 - 2}} = 0,48 + 4 = 4,48\Omega \]

Cường độ dòng điện qua mạch chính là: \[I = \frac{E}{{R + r}} = \frac{{6,6}}{{4,48 + 0,12}} = \frac{{33}}{{23}}A\]

Hiệu điện thế thực tế hai đầu đèn 1:

\[U{'_1} = I.{R_{d1 - d2 - 2}} = \frac{{33}}{{23}}.4 = \frac{{132}}{{23}}\]\[ = 5,74V < \;{U_{d1}} = 6V;\]Đèn 1 sáng yếu.

Cường độ dòng điện thực tế qua đèn 2:

\[I{'_2} = \frac{{U{'_1}}}{{{R_{d1 - d2 - 2}}}} = \frac{{\frac{{132}}{{23}}}}{6}\]\[ = 0,96A > \;{I_{d2}} = 0,5A\]

Nên đèn 2 sáng quá và dễ cháy.

Bài 57: Một ô tô khối lượng 2 tấn đang chuyển động trên đường ngang với vận tốc 72 km/h thì tài xế tắt máy. Bỏ qua lực cản không khí tác dụng lên xe. Lấy g = 10 m/s².

- Nếu tài xế không đạp phanh thì xe đi thêm 100 m rồi dừng lại.

- Nếu tài xế đạp phanh thì xe trượt thêm một đoạn 25 m rồi dừng lại. Coi chuyển động của xe là thẳng chậm dần đều. Tìm độ lớn lực ma sát lăn trong hai trường hợp?

Lời giải:

Xe chuyển động theo phương ngang nên \(N = P = mg = 10.2000 = 20000N\)

TH1: $a_1=\frac{v^2-{v_0}^2}{2s_1}=\frac{0-{20}^2}{2.100}=-2m/s^2$

$\begin{array}{l}-F_{ms1}=m{a}_1\Rightarrow -{\mu }_{1}N=m{a}_1\\ \Rightarrow {\mu }_1=\frac{-m{a}_1}{N}=\frac{-2000.(-2)}{20000}=0,2\end{array}$

TH2: $a_2=\frac{v^2-{v_0}^2}{2s_2}=\frac{0-{20}^2}{2.25}=-8m/s^2$

$-F_{ms2}=m{a}_2\Rightarrow -{\mu }_{2}N=m{a}_2$\( \Rightarrow {\mu _2} = \frac{{ - m{a_2}}}{N} = \frac{{ - 2000.( - 8)}}{{20000}} = 0,8\)

Bài 58: Một ô tô có khối lượng 2 tấn khi đi qua A có vận tốc 72 km/h  thì tài xế tắt máy, xe chuyển động chậm dần đều đến B thì có vận tốc 18 km/h. Biết quãng đường AB nằm ngang dài 100 m.

a, Xác định hệ số ma sát μ1 trên đoạn đường AB.

b, Đến B xe vẫn không nổ máy và tiếp tục xuống dốc nghiêng BC dài 50 m, biết dốc hợp với mặt phẳng nằm ngang một góc α = 300. Biết hệ số ma sát giữa bánh xe và dốc nghiêng là μ2 = 0,1. Xác định vận tốc của xe tại chân dốc nghiêng C. 

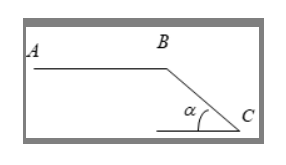
Lời giải:

Ta có:

\[{v_A} = 72(km/h) = 20(m/s)\]

\[{v_B} = 18(km/h) = 5(m/s)\]

Chọn mốc thế năng tại AB

Theo định luật bảo toàn năng lượng \[{{\rm{W}}_A} = {{\rm{W}}_B} + {A_{ms}}\]

\[{{\rm{W}}_A} = \frac{1}{2}m{v^2}_A = \frac{1}{2}{.2000.20^2} = {4.10^5}(J)\]

\[{{\rm{W}}_B} = \frac{1}{2}m{v^2}_B = \frac{1}{2}{.2000.5^2} = 25000(J)\]

\[{A_{ms}} = {\mu _1}.m.g.AB = {\mu _1}.2000.10.100 = {2.10^6}.{\mu _1}(J)\]

\[ \Rightarrow {4.10^5} = 25000 + {2.10^6}.{\mu _1} \Rightarrow {\mu _1} = 0,1875\]

b, Chọn mốc thế năng tại C: \[{z_B} = BC.\sin {30^0} = 50.0,5 = 25(m)\]

\[{{\rm{W}}_B} = {{\rm{W}}_C} + {A_{ms}}\]

\[{{\rm{W}}_B} = \frac{1}{2}m{v^2}_B + mg{z_B} = \frac{1}{2}{.2000.5^2} + 2000.10.25 = 525000(J)\]

\[{{\rm{W}}_C} = \frac{1}{2}m{v^2}_C = \frac{1}{2}.2000.v_C^2 = 1000v_C^2(J)\]

\[{A_{ms}} = {\mu _2}mg\cos \alpha .BC = 0,1.2000.10.\frac{{\sqrt 3 }}{2}.50 = 86602,54(J)\]

\[ \Rightarrow 525000 = 1000{v^2}_C + 86602,54 \Rightarrow {v_C} = 20,94(m/s)\]

Bài 59: ​Một bình nhiệt lượng kế chứa nước có khối lượng nước m1 = 100 g đang ở nhiệt độ t1 = 25^oC. Người ta thả vào bình một quả cầu bằng kim loại có khối lượng m₂ = 100 g đang ở nhiệt độ t₂ = 100^oC. Nhiệt độ của hệ thống khi cân bằng nhiệt là t_cb = 30^oC. Sau đó người ta đổ thêm vào bình một lượng nước có khối lượng m₃ = 200 g cũng có nhiệt độ là t₁ = 25^oC thì nhiệt độ của hệ thống khi cân bằng nhiệt là tcb = 27,5^oC. Cho biết c₁ = 4200 J/Kg.K. Bỏ qua sự trao đổi nhiệt của hệ thống với môi trường bên ngoài. Bình nhiệt lượng kế có thu và tỏa nhiệt. Tính nhiệt dung riêng c₂ của kim loại chế tạo quả cầu.

Lời giải:

Gọi c₀, m₀ là nhiệt dung riêng và khối lượng của nhiệt lượng kế.

*Quá trình 1

Nhiệt lượng mà nước và nhiệt lượng kế thu vào: \({Q_1} = \left( {{m_1}{c_1} + {m_0}{c_0}} \right)\left( {{t_{cb}} - {t_1}} \right)\)

\({Q_1} = \left( {0,1.4200 + {m_0}{c_2}} \right)\left( {30 - 25} \right) = 5\left( {420 + {m_0}{c_0}} \right)\)

Nhiệt lượng do quả cầu tỏa ra: \({Q_2} = {m_2}{c_2}\left( {{t_2} - {t_{cb}}} \right) = 0,1.{c_2}.\left( {100 - 30} \right) = 7{c_2}\) (J)

Phương trình cân bằng nhiệt: \({Q_1} = {Q_2} \Leftrightarrow 5\left( {420 + {m_0}{c_0}} \right) = 7{c_2}\) (1)

*Quá trình 2

Nhiệt lượng do nước đổ thêm vào thu vào

\[{Q_3} = {m_3}.{c_1}.\left( {t{'_{cb}} - {t_3}} \right) = 0,2.4200.(27,5 - 25) = 2100(J)\]

Nhiệt lượng do nước, nhiệt lượng kế, quả cầu tỏa ra:

\[{Q_4} = \left( {{m_1}{c_1} + {m_0}{c_0} + 0,1.{c_2}} \right)\left( {{t_{cb}} - t{'_{cb}}} \right)\]

\[ \Rightarrow {Q_4} = \left( {0,1.4200 + {m_o}{c_o} + 0,1{c_2}} \right)\left( {30 - 27,5} \right)\]

\[ \Rightarrow {Q_4} = (420 + {m_0}{c_0}).2,5 + 0,1.2,5.{c_2}\] (2)

Thay (1) vào (2) \[ \Rightarrow {Q_4} = \frac{{7{c_2}}}{5}.2,5 + 0,25.{c_2} = 3,75{c_2}\]

Phương trình cân bằng nhiệt: \[{Q_4} = {Q_3} \Leftrightarrow 3,75{c_2} = 2100 \Leftrightarrow {c_2} = 560(J/kg.k)\]

Bài 60: Một nhiệt lượng kế khối lượng m₁ = 100 g, chứa một lượng m₂ = 500 g nước ở cùng nhiệt độ t₁ = 15°C. Người ta thả vào một hợp kim nhôm-thiếc có khối lượng 150 g có nhiệt độ là t₂ = 100°C. Khi cân bằng nhiệt hệ có nhiệt độ là t = 17^oC. Tính khối lượng m₃ của nhôm, m₄ của thiếc có trong hợp kim. Cho nhiệt dung riêng của chất làm nhiệt lượng kế, nước, nhôm, và của thiếc lần lượt là c₁ = 460 J/kg.K; c₂ = 4200 J/kg.K; c₃ = 900 J/kg.K, c₄ = 230 J/kg.K.

Lời giải:

Nhiệt lượng do nhôm tỏa ra: \[{Q_3} = {m_3}.{c_3}.({t_2} - t)\]

Nhiệt lượng do thiếc tỏa ra: \[{Q_4} = {m_4}.{c_4}.({t_2} - t)\]

Nhiệt lượng do nhiệt lượng kế hấp thụ: \[{Q_1} = {m_1}.{c_1}.(t - {t_1})\]

Nhiệt lượng do nước hấp thụ:\[{Q_4} = {m_4}.{c_4}.({t_2} - t)\] \[{Q_2} = {m_2}.{c_2}.(t - {t_1})\]

Khi cân bằng nhiệt:

\[{Q_1} + {Q_2} = {Q_3} + {Q_4} \Rightarrow ({m_1}{c_1} + {m_2}{c_2})(t - {t_1}) = ({m_3}.{c_3} + {m_4}.{c_4})({t_2} - t)\]

\[ \Rightarrow {m_3}.{c_3} + {m_4}.{c_4} = \frac{{({m_1}{c_1} + {m_2}{c_2})(t - {t_1})}}{{{t_2} - t}}\]

\[ \Rightarrow {m_3}.{c_3} + {m_4}.{c_4} = \frac{{(0,1.460 + 0,5.4200)(17 - 15)}}{{100 - 17}} = 51,7\]

Ta có hệ: \[\left\{ \begin{array}{l}{m_3} + {m_4} = 0,15\\900{m_3} + 230{m_4} = 51,17\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m_3} = 0,025\\{m_4} = 0,125\end{array} \right.\]

Bài 61: Cho hệ vật như hình vẽ với khối lượng lần lượt là m₁ = 3 kg, m₂ = 2 kg, α = 300. Ban đầu m₁ được giữ ở vị trí thấp hơn m₂ một đoạn h = 0,75 m. Thả cho 2 vật chuyển động. Bỏ qua ma sát và khối lượng ròng rọc và dây. Lấy g = 10 m/s². Tính lực nén lên trục ròng rọc.

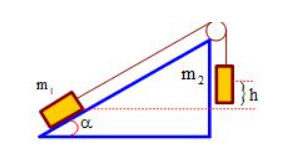
A. 8 N.

B. 10 N.

C. 22 N.

D. 31,2 N.

Lời giải:

Đáp án D

+ Theo định luật II Niwton: $\left\{\begin{array}{l}\overrightarrow{P_1}+\overrightarrow{N_1}+\overrightarrow{T_1}=m_1\overrightarrow{a_1}\left(1\right)\\ \overrightarrow{P_2}+\overrightarrow{T_2}=m_2\overrightarrow{a_2}\left(2\right)\end{array}\right.$

+ Chiếu (1) và (2) theo thứ tự lên hướng chuyển động của m1 và m2

$\Rightarrow \left\{\begin{array}{l}-P_2\sin \alpha +T_1=m_1{a}_1\\ P_2-T_2=m_2{a}_2\end{array}\right.$ với \({a_1} = {a_2} = a;{T_1} = {T_2} = T\)

•  Gia tốc chuyển động: \[a = \frac{{{m_2} - {m_1}\sin \alpha }}{{{m_1} + {m_2}}}.g = 1\,\,m/{s^2}\]

•  Lực căng của dây: \[T = {m_2}(g - a) = 18N\]

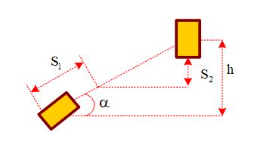
+ Gọi quãng đường của mỗi vật là: \[{s_1} = {s_2} = s\]

Khi 2 vật ở ngang nhau: 

$\begin{array}{l}{s}_1\sin \alpha +s_2=h\\ \Rightarrow s(\sin \alpha +1)=h\\ \Rightarrow s=\frac{h}{\sin \alpha +1}=0,5m\end{array}$

+ Lực nén: Dây nén lên ròng rọc 2 lực căng $\overrightarrow{T_1}=T{\text{'}}_2=T=18N$

+ Góc tạo bởi \[T{'_1}\] và $\overrightarrow{T_2}:\beta ={90}^0-\alpha ={60}^0$

+ Lực nén lên ròng rọc: $\overrightarrow{F}=\overrightarrow{T{\text{'}}_1}+\overrightarrow{T{\text{'}}_2}$

$F=2T.\cos \frac{\beta }{2}=18\sqrt{3}\approx 31,2N$

Bài 62: Cho hệ như hình vẽ với khối lượng của vật một và vật hai lần lượt là m₁ = 3 kg; m₂ = 2 kg, hệ số ma sát giữa hai vật và mặt phẳng nằm ngang là μ = μ₁ = μ₂ = 0,1. Tác dụng một lực F = 10 N vào vật một hợp với phương ngang một góc. Lấy g = 10 m/s². Tính gia tốc chuyển động và lực căng của dây.

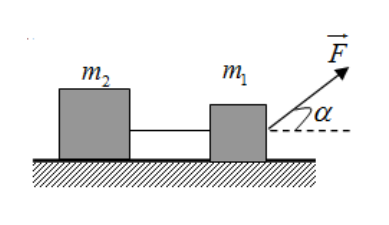
Lời giải:

Phân tích các lực tác dụng lên hệ vật

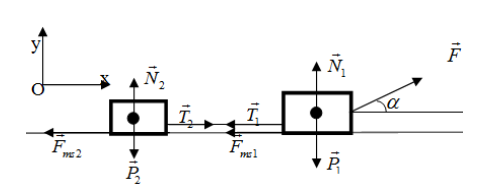
Chọn hệ quy chiếu như hình vẽ, chiều dương (+) là chiều chuyển động

Xét vật 1: Áp dụng định luật II Newton ta có $\overrightarrow{F}+{\overrightarrow{F}}_{ms1}+\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{T_1}=m_1\overrightarrow{a}$

Chiếu lên Ox: $F\cos \alpha -F_{ms1}-T_1=m_{1}a$ (1)

Chiếu lên Oy: $N_1-P_1+F\sin \alpha =0\Rightarrow N_1=m_{1}g-F\sin \alpha$

Thay vào (1) ta được: $F\cos \alpha -\mu (m_{1}g-F\sin \alpha )-T_1=m_{1}a$

Tương tự đối với vật 2: ${\overrightarrow{F}}_{ms2}+\overrightarrow{N_2}+{\overrightarrow{P}}_2+{\overrightarrow{T}}_2=m_2\overrightarrow{a}$

Chiếu lên Ox: \[ - {F_{ms2}} + {T_2} = {m_2}a\] (2)

Chiếu lên Oy: \[{N_2} = {P_2} = {m_2}g\]

Thay vào (2) ta được  \[ - \mu {m_2}g + {T_2} = {m_2}a\]

Vì dây không dãn nên \[T = {T_1} = {T_2}\]

$\left\{\begin{array}{l}F\cos \alpha -\mu (m_{1}g-F\sin \alpha )-T_1=m_{1}a\\ -\mu m_{2}g+T_2=m_{2}a\end{array}\right.$

Cộng vế ta có: $F\cos \alpha -\mu (m_{1}g-F\sin \alpha )-\mu m_{2}g=(m_1+m_2)a$

$\Rightarrow a=\frac{F\cos \alpha -\mu (m_{1}g-F\sin \alpha )-\mu m_{2}g}{m_1+m_2}$

\[ \Rightarrow a = \frac{{10.\cos {{30}^0} - 0,1(3.10 - 10.\sin {{30}^0}) - 0,1.2.10}}{{3 + 2}}\]\[ = 0,832(m/{s^2})\]

Thay vào (**) ta có \[T = {m_2}a + \mu {m_2}g = 2.0,832 + 0,1.2.10 = 3,664(N)\]

Bài 63: Con lắc đơn đang đứng yên ở vị trí cân bằng. Lúc t = 0 truyền cho con lắc vận tốc v₀ = 20 cm/s nằm ngang theo chiều dương thì nó dao động điều hoà với chu kì \[T = \frac{{2\pi }}{5}\] s. Phương trình dao động của con lắc dạng li độ góc là

A. α = 0,1cos(5t - π/2) (rad).

B. α = 0,1sin(5t + π) (rad).

C. α = 0,1sin(t/5 - π) (rad).

D. α = 0,1sin(t/5 + π) (rad).

Lời giải: 

Đáp án A

$\omega =\frac{2\pi }{T}=\sqrt{\frac{g}{\mathcal{l}}}=5\Rightarrow \mathcal{l}= 0,4m$

Tại VTCB truyền cho vật vận tốc \[{v_0} \Rightarrow {v_0} = {v_{\max }}\]

\[ \Rightarrow {S_o} = \;\frac{{{v_{\max }}}}{\omega } = \frac{{20}}{5} = 4{\rm{ }}cm = 0,04{\rm{ }}m\]

Mặt khác: \[{S_o} = \ell \;{\alpha _0} \Leftrightarrow \;0,04 = \;{\alpha _0}.0,4\]\[ \Rightarrow {\alpha _0} = 0,1{\rm{ }}rad\]

Tại VTCB vật ở VTCB đi theo chiều dương $\Rightarrow \phi =-\frac{\pi }{2}$

$\Rightarrow \alpha =0,1cos\left(5t-\pi /2\right)\left(rad\right).$

Bài 64: Cho mạch điện U = 6 V; R = 2 Ω; Đèn 3 V – 3 W.

a. Tính Rđ và Iđm của đèn. Đèn có sáng bình thường không? Tại sao?

b. Để đèn sáng bình thường, phải mắc thêm Rx như thế nào? Tính Rx?

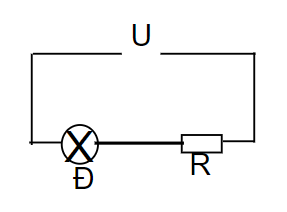
Lời giải:

a)

Lúc này điện trở tương đương của mạch là: \[{R_{td}} = R + {R_d} = 2 + 3 = 5(\Omega )\]

\[ \Rightarrow \]Cường độ dòng điện qua đèn là: \[I = \frac{U}{{{R_{td}}}} = \frac{6}{5} = 1,2(A)\]

Vì đèn sáng mạnh hơn bình thường.

b) Để đèn sáng bình thường thì cường độ dòng điện qua đèn = cường độ dòng điện định mức đèn (1A)

\[ \Rightarrow \]I' = 1A mà U không đổi $=>R{\text{'}}_{td}=\frac{U}{I\text{'}}=6\left(\Omega \right)$

Mà $R_{td}=5\left(\Omega \right)$ => Ta phải mắc thêm \[{R_x}\] nối tiếp vào mạch điện trên

$R_x=R{\text{'}}_{td}-R_{td}=6-5=1\left(\Omega \right)$

Bài 65: Một sợi dây đàn hồi dài 100 cm, có hai đầu A, B cố định. Một sóng truyền với tốc độ trên dây là 25 m/s, trên dây đếm được 3 nút sóng, không kể 2 nút A, B. Tần số dao dộng trên dây là

A. 50 Hz.

B. 100 Hz.

C. 25 Hz.

D. 20 Hz.

Lời giải:

Đáp án A

Trên dây có 3 nút sóng \( \Rightarrow k = 2\)

Tần số dao động trên dây là  \(f = \frac{{kv}}{{2\ell }} = \frac{{2.25}}{1} = 50Hz\)