Giải Toán 8 Bài 3: Những hằng đẳng thức đáng nhớ

hoa Ngày: 23-09-2022 Lớp 8

1.8 K

Tailieumoi.vn giới thiệu Giải bài tập Toán 8 Bài 3: Những hằng đẳng thức đáng nhớ, chi tiết nhất giúp học sinh dễ dàng làm bài tập Những hằng đẳng thức đáng nhớ lớp 8.

Giải bài tập Toán lớp 8 Bài 3: Những hằng đẳng thức đáng nhớ

Trả lời câu hỏi giữa bài

Trả lời câu hỏi 1 trang 9 sgk Toán 8 Tập 1: Với a và b là hai số bất kì, thực hiện phép tính (a+b)(a+b)

Phương pháp giải: Áp dụng quy tắc nhân đa thức với đa thức.

Lời giải:

$(a + b) (a + b)$

$= a (a + b) + b (a + b)$

$= a . a + a . b + b . a + b . b$

$= a^{2} + a b + a b + b^{2}$

$= a^{2} + (a b + a b) + b^{2}$

$= a^{2} + 2 a b + b^{2}$

Trả lời câu hỏi 2 trang 9 sgk Toán 8 Tập 1. Phát biểu hằng đẳng thức (1) bằng lời.

Áp dụng:

a) Tính $(a + 1)^{2}$

b) Viết biểu thức $x^{2} + 4 x + 4$ dưới dạng bình phương của một tổng

c) Tính nhanh: $51^{2}; 301^{2}$

Phương pháp giải: Hằng đẳng thức

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$ (1) $A, B$ là các biểu thức tùy ý.

Lời giải:

Phát biểu: Bình phương của tổng hai biểu thức bằng bình phương biểu thức thứ nhất cộng hai lần tích hai biểu thức đó cộng bình phương biểu thức thứ hai.

Áp dụng:

$\begin{array}{l} a) {(a + 1)}^{2} = a^{2} + 2 a + 1 \\ b) x^{2} + 4 x + 4 = x^{2} + 2.2 x + 2^{2} \\ = {(x + 2)}^{2} \\ c) 51^{2} = {(50 + 1)}^{2} \\ = 50^{2} + 2.50.1 + 1^{2} \\ = 2500 + 100 + 1 \\ = 2601 \\ 301^{2} = {(300 + 1)}^{2} \\ = 300^{2} + 2.300.1 + 1^{2} \\ = 90000 + 600 + 1 \\ = 90601 \end{array}$

Trả lời câu hỏi 3 trang 10 sgk Toán 8 Tập 1. Tính

{[a + (- b)]}^{2}

(với

a, b

là các số tùy ý).

Phương pháp giải: Áp dụng hằng đẳng thức (1)

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

Lời giải:

Áp dụng hằng đẳng thức (1) ta có:

$\begin{aligned} {[a + (- b)]}^{2} = a^{2} + 2. a . (- b) + {(- b)}^{2} \\ = a^{2} - 2 a b + b^{2} \end{aligned}$

Trả lời câu hỏi 4 trang 10 sgk Toán 8 Tập 1. Phát biểu hằng đẳng thức (2) bằng lời.

Áp dụng:

a) Tính ${(x - \frac{1}{2})}^{2}$

b) Tính $(2 x - 3 y)^{2}$

c) Tính nhanh $99^{2}$

Phương pháp giải: ${(A - B)}^{2} = A^{2} - 2 A B + B^{2}$ (2) $A, B$ là các biểu thức tùy ý.

Lời giải:

Phát biểu: Bình phương của hiệu hai biểu thức bằng bình phương biểu thức thứ nhất trừ hai lần tích hai biểu thức đó cộng bình phương biểu thức thứ hai.

Áp dụng:

$\begin{array}{l} a) {(x - \frac{1}{2})}^{2} = x^{2} - 2. x . \frac{1}{2} + {(\frac{1}{2})}^{2} \\ = x^{2} - x + \frac{1}{4} \\ b) {(2 x - 3 y)}^{2} = {(2 x)}^{2} - 2.2 x .3 y + {(3 y)}^{2} \\ = 4 x^{2} - 12 x y + 9 y^{2} \\ c) 99^{2} = {(100 - 1)}^{2} = 100^{2} - 2.100.1 + 1^{2} \\ = 10000 - 200 + 1 \\ = 9801 \end{array}$

Trả lời câu hỏi 5 trang 10 sgk Toán 8 Tập 1. Thực hiện phép tính

(a + b) (a - b)

(với

a, b

là các số tùy ý).

Phương pháp giải: Áp dụng quy tắc nhân đa thức với đa thức.

Lời giải:

$\begin{aligned} (a + b) (a - b) \\ = a (a - b) + b (a - b) \\ = a . a + a . (- b) + b . a + b . (- b) \\ = a^{2} - a b + a b - b^{2} \\ = a^{2} + (- a b + a b) - b^{2} \\ = a^{2} - b^{2} \end{aligned}$

Trả lời câu hỏi 6 trang 10 sgk Toán 8 Tập 1: Phát biểu hằng đẳng thức (3) bằng lời.

Áp dụng:

a) Tính $(x + 1) (x - 1)$

b) Tính $(x - 2 y) (x + 2 y)$

c) Tính nhanh $56.64$

Phương pháp giải: $A^{2} - B^{2} = (A + B) (A - B)$ (3) $A, B$ là các biểu thức tùy ý.

Lời giải:

Phát biểu: Hiệu của bình phương hai biểu thức bằng tích của tổng hai biểu thức và hiệu hai biểu thức.

Áp dụng:

$\begin{array}{l} a) (x + 1) (x - 1) = x^{2} - 1^{2} = x^{2} - 1 \\ b) (x - 2 y) (x + 2 y) \\ = x^{2} - {(2 y)}^{2} = x^{2} - 4 y^{2} \\ c) 56.64 = (60 - 4) (60 + 4) \\ = 60^{2} - 4^{2} = 3600 - 16 \\ = 3584 \end{array}$

Trả lời câu hỏi 7 trang 11 sgk Toán 8 Tập 1: Ai đúng, ai sai?

Đức viết:

$x^{2} - 10 x + 25 = {(x - 5)}^{2}$

Thọ viết:

$x^{2} - 10 x + 25 = {(5 - x)}^{2}$ .

Hương nêu nhận xét: Thọ viết sai, Đức viết đúng.

Sơn nói: Qua ví dụ trên mình rút ra được một hằng đẳng thức rất đẹp !

Hãy nêu ý kiến của em. Sơn rút ra được hằng đẳng thức nào?

Phương pháp giải: Áp dụng tính chất giao hoán của phép cộng

Lời giải:

- Đức và Thọ đều viết đúng;

- Hương nhận xét sai;

- Sơn rút ra được hằng đẳng thức là: ${(x - 5)}^{2} = {(5 - x)}^{2}$

Ta có:

$\begin{aligned} x^{2} - 10 x + 25 = 25 - 10 x + x^{2} \\ \Rightarrow {(x - 5)}^{2} = {(5 - x)}^{2} \end{aligned}$

Câu hỏi và bài tập (trang 11, 12 sgk Toán 8 Tập 1)

Bài 16 trang 11 sgk Toán 8 Tập 1: Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu;a) $x^{2} + 2 x + 1$ ;b) $9 x^{2} + y^{2} + 6 x y$ ;c) $25 a^{2} + 4 b^{2} - 20 a b$ ;

d) $x^{2} - x + \frac{1}{4}$ .

Phương pháp giải: Áp dụng: Bình phương của một tổng: ${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

Lời giải:

a) $x^{2} + 2 x + 1$

$= x^{2} + 2. x .1 + 1^{2} = {(x + 1)}^{2}$

b) $9 x^{2} + y^{2} + 6 x y$

$= 9 x^{2} + 6 x y + y^{2}$ $= {(3 x)}^{2} + 2.3 x . y + y^{2} = {(3 x + y)}^{2}$

c) $25 a^{2} + 4 b^{2} - 20 a b$

$= 25 a^{2} - 20 a b + 4 b^{2}$

$= {(5 a)}^{2} - 2.5 a .2 b + {(2 b)}^{2}$

$= {(5 a - 2 b)}^{2}$

Hoặc

$25 a^{2} + 4 b^{2} - 20 a b$

$= 4 b^{2} - 20 a b + 25 a^{2}$

$= {(2 b)}^{2} - 2.2 b .5 a + {(5 a)}^{2}$

$= {(2 b - 5 a)}^{2}$

d) $x^{2} - x + \frac{1}{4}$

$= x^{2} - 2. x . \frac{1}{2} + {(\frac{1}{2})}^{2}$

$= {(x - \frac{1}{2})}^{2}$

Hoặc

$x^{2} - x + \frac{1}{4} = \frac{1}{4} - x + x^{2}$

$= {(\frac{1}{2})}^{2} - 2. \frac{1}{2} . x + x^{2}$ $= {(\frac{1}{2} - x)}^{2}$

Bài 17 trang 11 sgk Toán 8 Tập 1: Chứng minh rằng:

${(10 a + 5)}^{2} = 100 a . (a + 1) + 25.$

Từ đó em hãy nêu cách tính nhẩm bình phương của một số tự nhiên có tận cùng bằng chữ số $5.$

Áp dụng để tính: $25^{2}; 35^{2}; 65^{2}; 75^{2} .$

Phương pháp giải: Áp dụng: Bình phương một tổng: ${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

Lời giải:

Ta có:

$\begin{aligned} {(10 a + 5)}^{2} = {(10 a)}^{2} + 2.10 a .5 + 5^{2} \\ = 100 a^{2} + 100 a + 25 \\ = 100 a (a + 1) + 25. \end{aligned}$

* Cách để tính nhẩm bình phương của một số tự nhiên có tận cùng bằng chữ số $5$ là:

Bước 1: Tìm số tự nhiên $a$ , sao cho số đã cho viết được dưới dạng $10 a + 5$ tức là có dạng $\bar{a 5}$ (chẳng hạn số $25$ thì $a = 2$ )

Bước 2: Lấy $a$ nhân với $a + 1$ và nhân với $100$ , rồi cộng với $25$ .

Áp dụng tính:

$25^{2}$ , ta được $a = 2$ nên $25^{2} = 2. (2 + 1) .100 + 25 = 625;$

$35^{2}$ , ta được $a = 3$ nên $35^{2} = 3. (3 + 1) .100 + 25 = 1225$

Tương tự:

$65^{2} = 6. (6 + 1) .100 + 25 = 4225$

$75^{2} = 7. (7 + 1) .100 + 25 = 5625.$

Bài 18 trang 11 sgk Toán 8 Tập 1: Hãy tìm cách giúp bạn An khôi phục lại những hằng đẳng thức bị mực làm nhòe đi một số chỗ:

a) $x^{2} + 6 x y + \dots = {(\dots + 3 y)}^{2}$ ;

b) $. . . - 10 x y + 25 y^{2} = {(\dots - \dots)}^{2}$ ;

Hãy nêu một số đề bài tương tự.

Phương pháp giải: Áp dụng bình phương của một tổng, bình phương của một hiệu.

Lời giải:

a) $x^{2} + 6 x y + \dots = {(\dots + 3 y)}^{2}$

Suy ra $x^{2} + 2. x .3 y + . . . = {(. . . + 3 y)}^{2}$

Nhận thấy đây là hằng đẳng thức thứ nhất $(A + B)^{2} = A^{2} + 2 A B + B^{2}$ với $A = x$ và $2 A B = 2. x .3 y$

Suy ra $B = 3 y$ .

Từ đó, ta có: $x^{2} + 2. x .3 y + {(3 y)}^{2} = {(x + 3 y)}^{2}$

Vậy: $x^{2} + 6 x y + 9 y^{2} = {(x + 3 y)}^{2}$

b) $. . . - 10 x y + 25 y^{2} = {(\dots - \dots)}^{2}$

Suy ra $. . . - 2. x .5 y + {(5 y)}^{2} = {(. . . - . . .)}^{2}$

Nhận thấy đây là hằng đẳng thức thứ hai $(A - B)^{2} = A^{2} - 2 A B + B^{2}$ với $B = 5 y$ và $2 A B = 2. x .5 y$

Suy ra $A = x$ .

Do đó, ta có: $x^{2} - 2. x .5 y + {(5 y)}^{2} = {(x - 5 y)}^{2}$

Vậy: $x^{2} - 10 x y + 25 y^{2} = {(x - 5 y)}^{2}$

Đề bài tương tự:

$4 + 4 y + \dots = {(\dots + y)}^{2}$

Có: $2^{2} + 2.2. y + y^{2} = {(2 + y)}^{2}$

$\Rightarrow 4 + 4 y + y^{2} = {(2 + y)}^{2}$

Bài 19 trang 12 sgk Toán 8 Tập 1: Đố: Tính diện tích phần hình còn lại mà không cần đo.

Từ một miếng tôn hình vuông có cạnh bằng $a + b$ , bác thợ cắt đi một miếng cũng hình vuông có cạnh bằng $a - b$ (cho $a > b$ ). Diện tích phần hình còn lại là bao nhiêu? Diện tích phần hình còn lại có phụ thuộc vào vị trí cắt không?

Phương pháp giải: Biểu diễn phần diện tích còn lại của miếng tôn theo $a, b .$

- Áp dụng:

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

${(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

Lời giải:

Diện tích của miếng tôn hình vuông ban đầu là ${(a + b)}^{2}$

Diện tích của miếng tôn hình vuông phải cắt là ${(a - b)}^{2}$ .

Phần diện tích miếng tôn còn lại là ${(a + b)}^{2} - {(a - b)}^{2}$ .

Ta có:

$\begin{aligned} {(a + b)}^{2} - {(a - b)}^{2} \\ = a^{2} + 2 a b + b^{2} - (a^{2} - 2 a b + b^{2}) \\ = a^{2} + 2 a b + b^{2} - a^{2} + 2 a b - b^{2} \\ = (a^{2} - a^{2}) + (b^{2} - b^{2}) + (2 a b + 2 a b) \\ = 4 a b \end{aligned}$

Vậy phần diện tích hình còn lại là $4 a b$ và không phụ thuộc vào vị trí cắt.

Hoặc ta có thể áp dụng hằng đẳng thức thứ 3 để tính như sau:

$\begin{array}{l} {(a + b)}^{2} - {(a - b)}^{2} \\ = (a + b + a - b) [a + b - (a - b)] \\ = 2 a . (a + b - a + b) \\ = 2 a .2 b \\ = 4 a b \end{array}$

Bài 20 trang 12 sgk Toán 8 Tập 1: Nhận xét sự đúng, sai của kết quả sau:

$x^{2} + 2 x y + 4 y^{2} = {(x + 2 y)}^{2}$

Phương pháp giải: Áp dụng bình phương của một tổng.

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

Lời giải:

Ta có:

$\begin{aligned} {(x + 2 y)}^{2} = x^{2} + 2. x .2 y + (2 y)^{2} \\ = x^{2} + 4 x y + 4 y^{2} \end{aligned}$

Do đó kết quả $x^{2} + 2 x y + 4 y^{2} = {(x + 2 y)}^{2}$ là sai.

Bài 21 trang 12 sgk Toán 8 Tập 1: Viết các đa thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a) $9 x^{2} - 6 x + 1$ ;

b) ${(2 x + 3 y)}^{2} + 2. (2 x + 3 y) + 1$ .

Hãy nêu một đề bài tương tự.

Phương pháp giải: Áp dụng bình phương của một tổng, bình phương của một hiệu.

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

${(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

Lời giải:

a) $9 x^{2} - 6 x + 1 = {(3 x)}^{2} - 2.3 x .1 + 1^{2}$ $= {(3 x - 1)}^{2}$

Hoặc

$9 x^{2} - 6 x + 1 = 1 - 6 x + 9 x^{2}$ $= 1^{2} - 2.1.3 x + {(3 x)}^{2} = {(1 - 3 x)}^{2}$

b) ${(2 x + 3 y)}^{2} + 2. (2 x + 3 y) + 1$ $= {(2 x + 3 y)}^{2} + 2. (2 x + 3 y) .1 + 1^{2}$

Áp dụng hằng đẳng thức thứ nhất $A^{2} + 2 A B + B^{2} = {(A + B)}^{2}$ với $A = 2 x + 3 y$ ; $B = 1$ ta được:

${(2 x + 3 y)}^{2} + 2. (2 x + 3 y) + 1$

$= {(2 x + 3 y)}^{2} + 2. (2 x + 3 y) .1 + 1^{2}$

$= {[(2 x + 3 y) + 1]}^{2} = {(2 x + 3 y + 1)}^{2}$

Đề bài tương tự. Chẳng hạn:

$1 + 2 (x + 2 y) + {(x + 2 y)}^{2}$ ;

$4 x^{2} - 12 x + 9$ ; …

Bài 22 trang 12 sgk Toán 8 Tập 1: Tính nhanh

a) $101^{2};$ b) $199^{2}$ ; c) 47.53

Phương pháp giải:

Áp dụng:

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

Lời giải:

$\begin{aligned} 101^{2} = {(100 + 1)}^{2} \\ = 100^{2} + 2.100.1 + 1^{2} \\ = 10000 + 200 + 1 \\ = 10201 \end{aligned}$

$\begin{aligned} 199^{2} = {(200 - 1)}^{2} \\ = 200^{2} - 2.200.1 + 1^{2} \\ = 40000 - 400 + 1 = 39601 \end{aligned}$

$\begin{aligned} 47.53 = (50 - 3) (50 + 3) \\ = 50^{2} - 3^{2} = 2500 - 9 = 2491 \end{aligned}$

Bài 23 trang 12 sgk Toán 8 Tập 1: Chứng minh rằng:

${(a + b)}^{2} = {(a - b)}^{2} + 4 a b;$

${(a - b)}^{2} = {(a + b)}^{2} - 4 a b .$

Áp dụng:

a) Tính ${(a - b)}^{2}$ , biết $a + b = 7$ và $a . b = 12.$

b) Tính ${(a + b)}^{2}$ , biết $a - b = 20$ và $a . b = 3.$

Phương pháp giải: Áp dụng bình phương của một tổng, bình phương của một hiệu để biến đổi vế trái hoặc vế phải của từng đẳng thức, đưa về bằng vế còn lại.

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

${(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

Lời giải:

* ${(a + b)}^{2} = {(a - b)}^{2} + 4 a b$

Cách 1: Biến đổi vế trái:

$\begin{aligned} {(a + b)}^{2} = a^{2} + 2 a b + b^{2} \\ = a^{2} - 2 a b + b^{2} + 4 a b \\ = (a^{2} - 2 a b + b^{2}) + 4 a b \\ = {(a - b)}^{2} + 4 a b \end{aligned}$

Vậy ${(a + b)}^{2} = {(a - b)}^{2} + 4 a b$

Cách 2: Biến đổi vế phải:

$\begin{aligned} {(a - b)}^{2} + 4 a b \\ = a^{2} - 2 a b + b^{2} + 4 a b \\ = a^{2} + (4 a b - 2 a b) + b^{2} \\ = a^{2} + 2 a b + b^{2} \\ = (a + b)^{2} \end{aligned}$

Vậy ${(a + b)}^{2} = {(a - b)}^{2} + 4 a b$

Cách 3:

$\begin{array}{l} (a + b)^{2} = (a - b)^{2} + 4 a b \\ \Leftrightarrow (a + b)^{2} - (a - b)^{2} - 4 a b = 0 \\ \Leftrightarrow [a + b - (a - b)] . [a + b + (a - b)] - 4 a b = 0 \\ \Leftrightarrow 2 b .2 a - 4 a b = 0 \\ \Leftrightarrow 4 a b - 4 a b = 0 \end{array}$

(Luôn đúng)

Vậy ${(a + b)}^{2} = {(a - b)}^{2} + 4 a b$

* ${(a - b)}^{2} = {(a + b)}^{2} - 4 a b$

Biến đổi vế phải:

$\begin{aligned} {(a + b)}^{2} - 4 a b \\ = a^{2} + 2 a b + b^{2} - 4 a b \\ = a^{2} + (2 a b - 4 a b) + b^{2} \\ = a^{2} - 2 a b + b^{2} = {(a - b)}^{2} \end{aligned}$

Vậy ${(a - b)}^{2} = {(a + b)}^{2} - 4 a b$

Áp dụng: Tính:

a) Với $a + b = 7$ và $a . b = 12$ ta có:

${(a - b)}^{2} = {(a + b)}^{2} - 4 a b$

$= 7^{2} - 4.12 = 49 - 48 = 1$

b) Với $a - b = 20$ và $a . b = 3$ ta có:

${(a + b)}^{2} = {(a - b)}^{2} + 4 a b$

$= 20^{2} + 4.3$

$= 400 + 12 = 412$

Bài 24 trang 12 sgk Toán 8 Tập 1: Tính giá trị của biểu thức

49 x^{2} - 70 x + 25

trong mỗi trường hợp sau:

a) $x = 5$ ; b) $x = \frac{1}{7}$ .

Phương pháp giải: Áp dụng bình phương của một hiệu, sau đó thay lần lượt từng giá trị của $x$ để tính giá trị của biểu thức.

Lời giải:

Ta có: $49 x^{2} - 70 x + 25$ $= {(7 x)}^{2} - 2.7 x .5 + 5^{2} = {(7 x - 5)}^{2}$

a) Với $x = 5$ ta có:

${(7.5 - 5)}^{2} = {(35 - 5)}^{2} = 30^{2} = 900$

b) Với $x = \frac{1}{7}$ ta có:

${(7. \frac{1}{7} - 5)}^{2} = {(1 - 5)}^{2} = {(- 4)}^{2} = 16$

Bài 25 trang 12 sgk Toán 8 Tập 1: Tính

a) ${(a + b + c)}^{2}$ ;

b) ${(a + b - c)}^{2}$ ;

c) ${(a - b - c)}^{2}$

Phương pháp giải:

Áp dụng bình phương của một tổng, bình phương của một hiệu.

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

${(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

Lời giải:

$\begin{aligned} {(a + b + c)}^{2} = {[(a + b) + c]}^{2} \\ = {(a + b)}^{2} + 2 (a + b) c + c^{2} \\ = a^{2} + 2 a b + b^{2} + 2 a c + 2 b c + c^{2} \\ = a^{2} + b^{2} + c^{2} + 2 a b + 2 b c + 2 a c \end{aligned}$

$\begin{aligned} {(a + b - c)}^{2} = {[(a + b) - c]}^{2} \\ = {(a + b)}^{2} - 2 (a + b) c + c^{2} \\ = a^{2} + 2 a b + b^{2} + (- 2) . a c + (- 2) . b c + c^{2} \\ = a^{2} + 2 a b + b^{2} - 2 a c - 2 b c + c^{2} \\ = a^{2} + b^{2} + c^{2} + 2 a b - 2 b c - 2 a c \end{aligned}$

$\begin{aligned} {(a - b - c)}^{2} = {[(a - b) - c]}^{2} \\ = {(a - b)}^{2} - 2 (a - b) c + c^{2} \\ = a^{2} - 2 a b + b^{2} + (- 2) . a c + (- 2) . (- b) . c + c^{2} \\ = a^{2} - 2 a b + b^{2} - 2 a c + 2 b c + c^{2} \\ = a^{2} + b^{2} + c^{2} - 2 a b + 2 b c - 2 a c \end{aligned}$

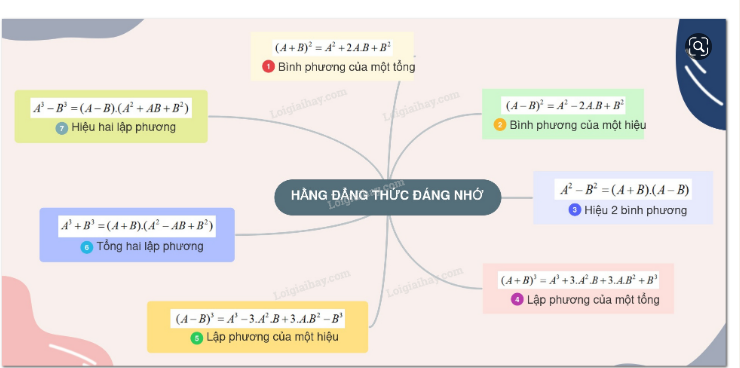
Lý thuyết những hằng đẳng thức đáng nhớ

1. Bình phương của một tổng: Bình phương của tổng hai biểu thức bằng bình phương biểu thức thứ nhất cộng hai lần tích hai biểu thức đó cộng bình phương biểu thức thứ hai.

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

$A, B$ là các biểu thức tùy ý.

2. Bình phương của một hiệu: Bình phương của hiệu hai biểu thức bằng bình phương biểu thức thứ nhất trừ hai lần tích hai biểu thức đó cộng bình phương biểu thức thứ hai.

${(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

$A, B$ là các biểu thức tùy ý.

3. Hiệu của hai bình phương: Hiệu của bình phương hai biểu thức bằng tích của tổng hai biểu thức và hiệu hai biểu thức.

$A^{2} - B^{2} = (A + B) (A - B)$

$A, B$ là các biểu thức tùy ý.

Các dạng toán cơ bản

Dạng 1: Rút gọn biểu thức

Phương pháp giải: Sử dụng các hằng đẳng thức và phép nhân đa thức để biến đổi.

Ví dụ:

Rút gọn biểu thức: $C = x^{2} - 10 x y + 25 y^{2} - {(x - 5 y)}^{2}$

Ta có:

$C = x^{2} - 10 x y + 25 y^{2} - {(x - 5 y)}^{2}$ $= x^{2} - 2. x .5 y + {(5 y)}^{2} - {(x - 5 y)}^{2}$ $= {(x - 5 y)}^{2} - {(x - 5 y)}^{2} = 0$

Dạng 2: Tìm $x$

Phương pháp giải: Sử dụng các hằng đẳng thức và phép nhân đa thức để biến đổi để đưa về dạng tìm $x$ thường gặp

Ví dụ: Tìm $x$ biết: ${(x + 4)}^{2} - (x - 1) (x + 1) = 16$ .

Ta có:

$\begin{array}{l} {(x + 4)}^{2} - (x - 1) (x + 1) = 16 \\ \Leftrightarrow x^{2} + 2. x .4 + 4^{2} - (x^{2} - 1) = 16 \\ \Leftrightarrow x^{2} + 8 x + 16 - x^{2} + 1 = 16 \\ \Leftrightarrow 8 x = 16 - 16 - 1 \\ \Leftrightarrow 8 x = - 1 \\ \Leftrightarrow x = - \frac{1}{8} \end{array}$