20 Bài tập Phân tích đa thức thành nhân tử (sách mới) có đáp án

20 Bài tập Phân tích đa thức thành nhân tử (sách mới) có đáp án – Toán 8

diep4602 Ngày: 14-07-2024 Lớp 8

33.2 K

Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Phân tích đa thức thành nhân tử, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Phân tích đa thức thành nhân tử. Mời các bạn đón xem:

Bài tập Toán 8 Phân tích đa thức thành nhân tử

A. Bài tập Phân tích đa thức thành nhân tử

Bài 1. Phân tích các đa thức sau thành nhân tử:

a) 3x² + xy;

b) 4x³ – x;

c) x² – 16 + xy – 4y;

d) 8x⁴ – x.

Hướng dẫn giải

a) 3x² + xy = x(3x + y);

b) 4x³ – x = x(4x² – 1) = x[(2x)² – 1²] = x(2x – 1)(2x + 1);

c) x² – 16 + xy – 4y = (x² – 16) + (xy – 4y)

= (x – 4)(x + 4) + y(x – 4)

= (x – 4)(x + 4 + y);

d) 8x⁴ – x = x(8x³ – 1) = x[(2x)³ – 1³]

= x(2x – 1)(4x² + 2x + 1).

Bài 2. Tìm x, biết:

a) 2x² + 2x = 0;

b) 3x³ – 3x = 0.

Hướng dẫn giải

a) Ta có: 2x² + 2x = 2x(x + 1)

Khi đó, 2x² + 2x = 0 thì 2x(x + 1) = 0.

TH1: 2x = 0, suy ra x = 0.

TH2: x + 1 = 0, suy ra x = – 1.

Vậy x = 0 hoặc x = – 1.

b) Ta có: 3x³ – 3x = 3x(x² – 1) = 3x(x – 1)(x + 1).

Khi đó 3x³ – 3x = 0 thì 3x(x + 1)(x – 1) = 0.

TH1: 3x = 0, suy ra x = 0.

TH2: x + 1 = 0, suy ra x = – 1.

TH3: x – 1 = 0, suy ra x = 1.

Vậy x = 0 hoặc x = – 1 hoặc x = 1.

Bài 3. Một khu vườn hình vuông có độ dài cạnh bằng 2x (mét). Người ta làm đường đi xung quanh khu vườn, có độ rộng như nhau và bằng y (mét).

a) Viết biểu thức tính diện tích S của đường đi bao quanh mảnh vườn theo x và y.

b) Phân tích S thành nhân tử rồi tính S khi x = 102 m, y = 4 m.

Lý thuyết Toán 8 Kết nối tri thức Lý thuyết Toán 8 Kết nối tri thức Bài 9: Phân tích đa thức thành nhân tử

Hướng dẫn giải

a) Diện tích khu vườn hình vuông là: (2x)² (m²).

Vì làm đường đi bao quanh khu vườn, mỗi bên có độ rộng y mét nên phần vườn không chứa đường đi là một hình vuông có cạnh là 2x – 2y (m).

Diện tích khu vườn hình vuông sau khi làm đường đi là: (2x – 2y)² (m²).

Diện tích đường đi bao quanh khu vườn là: S = (2x)² – (2x – 2y)² (m²).

b) Ta có:

S = (2x)² – (2x – 2y)²

= [2x – (2x – 2y)][2x + (2x – 2y)]

= (2x – 2x + 2y)(2x + 2x – 2y)

= 2y(4x – 2y)

= 4y(2x – y).

Thay x = 102 m, y = 4 m vào S ta được:

S = 4.4.(2.102 – 4) = 16.200 = 3 200 m².

Bài 4. Phân tích các đa thức sau thành nhân tử:

a) xy + 2y².

b) (x – 1)² + 3(1 – x).

c) (y + 6)² – 4.

d) 8x² + 32xy + 32y².

e) x⁵ – x².

g) x³ – 2x² + x – 2.

h) x³ – 3y³+ 3x²y – xy².

Hướng dẫn giải

a) xy + 2y²

= y . x + y . 2y

= y(x + 2y);

b) (x – 1)² + 3(1 – x)

= (x – 1)(x – 1) – 3(x – 1)

= (x – 1)(x – 1 – 3)

= (x – 1)(x – 4).

c) (y + 6)² – 4

= (y + 6)² – 2²

= (y + 6 – 2)(y + 6 + 2)

= (y + 4)(y + 8);

d) 8x² + 32xy + 32y²

= 8(x² + 4xy + 4y²)

= 8[x² + 2 . x . 2y + (2y)²]

= 8(x + 2y)²;

e) x⁵ – x² = x² . x³ – x²

= x²(x³ – 1)

= x²(x – 1)(x² + x + 1).

g) x³ – 2x² + x – 2

= (x³ + x) – 2(x² + 1)

= x(x² + 1) – 2(x² + 1)

= (x² + 1)(x – 2);

h) x³ – 3y³+ 3x²y – xy²

= (x³ – xy²) + (3x²y – 3y³)

= x(x² – y²) + 3y(x² – y²)

= (x² – y²)(x + 3y)

= (x – y)(x + y)(x + 3y).

Bài 5. Phân tích các đa thức sau thành nhân tử rồi tính các giá trị của nó:

a) A = a(b + 3) – b(3 + b) tại a = 2023 và b = 2017.

b) B = x² – 2x + 1 – 4y² tại x = 51 và y = 25.

c) C = x² – 3y – 3x + xy tại x = 53 và y = 47.

Hướng dẫn giải

a) A = a(b + 3) – b(3 + b)

= (b + 3)(a – b)

Thay a = 2023 và b = 2017 vào biểu thức trên ta được:

A = (2017 + 3)(2023 – 2017)

= 2020 . 6 = 12 120.

b) B = x² – 2x + 1 – 4y²

= (x² – 2x + 1) – 4y²

= (x – 1)² – 4y²

= (x – 1 – 2y)(x – 1 + 2y)

Thay x = 51 và y = 25 vào biểu thức trên ta được:

B = (51 – 1 – 2.25)(51 – 1 + 2.25)

= 0.100 = 0.

c) C = x² – 3y – 3x + xy

= (x² – 3x) + (xy – 3y)

= x(x – 3) + y(x – 3)

= (x – 3)(x + y)

Thay x = 53 và y = 47 vào biểu thức trên ta được:

C = (53 – 3)(53 + 47) = 50 . 100 = 5 000.

Bài 6. Tìm x, biết:

a) (x – 3)² = (3 + x)².

b) 1 – 9x² = (3x + 1)².

c) x²(x + 8) + x² = –8x.

d) x² – 6x + 8 = 0.

Hướng dẫn giải

a) (x – 3)² = (3 + x)²

(x – 3) – (3 + x)² = 0

(x – 3 + 3 + x)(x – 3 – 3 – x) = 0

2x.(–6) = 0

2x = 0

x = 0.

Vậy x = 0.

b) 1 – 9x² = (3x + 1)²

(1 – 3x)(1 + 3x) – (3x + 1)² = 0

(3x + 1)(1 – 3x – 3x – 1) = 0

(3x + 1)(–6x) = 0

Suy ra 3x + 1 = 0 hoặc –6x = 0

3x = –1 hoặc x = 0

$x = - \frac{1}{3}$ hoặc x = 0.

Vậy 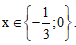Lý thuyết Toán 8 Chân trời sáng tạo Bài 4: Phân tích đa thức thành nhân tử .

c) x²(x + 8) + x² = –8x

x²(x + 8) + x² + 8x = 0

x²(x + 8) + x(x + 8) = 0

(x + 8)(x² + x) = 0

(x + 8).x.(x + 1) = 0

Suy ra x + 8 = 0 hoặc x = 0 hoặc x + 1 = 0

x = – 8 hoặc x = 0 hoặc x = –1.

Vậy x ∈ {–8; 0; –1}.

d) x² – 6x + 8 = 0.

x² – 2x – 4x + 8 = 0

x(x – 2) – 4(x – 2) = 0

(x – 2)(x – 4) = 0

Suy ra x – 2 = 0 hoặc x – 4 = 0

x = 2 hoặc x = 4.

Vậy x ∈ {2; 4}.

Bài 7.Cho x > 0. Tìm độ dài cạnh hình vuông có diện tích bằng 36x² + 60x + 25.

Hướng dẫn giải

Gọi cạnh hình vuông là a (a > 0)

Khi đó diện tích hình vuông là a²

Tức là 36x² + 60x + 25= a².

Ta sẽ phân tích đa thức 36x² + 60x + 25thành nhân tử có dạng a².

Ta có:

36x² + 60x + 25 = (6x)² + 2 . 6x . 5 + 5² = (6x + 5)²

Suy ra a² = (6x + 5)²

Do đó a = 6x + 5

Vậy độ dài cạnh hình vuông có diện tích bằng 36x² + 60x + 25 là 6x + 5.

Bài 8. Phân tích mỗi đa thức sau thành nhân tử:

a) 8x³ – 64 ;

b) x² – 25 – 4xy + 4y².

Hướng dẫn giải

a) 8x³ – 64 = (2x)³ – 4³ = (2x – 4)(4x² + 8x + 16).

b) x² – 25 – 4xy + 4y² = (x² – 4xy + 4y²) – 25

= (x – 2y)² – 25 = (x – 2y)² – 5²

= (x – 2y – 5)(x – 2y + 5).

Bài 9. Tính giá trị biểu thức sau:

A = x²y² + 2xyz + z² biết xy + z = 0.

Hướng dẫn giải

A = x²y² + 2xyz + z²

= (xy)² + 2xyz + z²= (xy + z)².

Thay xy + z = 0 vào biểu thức A ta được:

A = 0² = 0.

Vậy khi xy + z = 0 giá trị của biểu thức A bằng 0.

Vậy với xy + z = 0 thì A = 0.

Bài 10. Tìm x, biết:

a) x² – 4x = 0;

b) (x – 3)² + 3 – x = 0.

Hướng dẫn giải

a) x² – 4x = 0

$\Leftrightarrow$ x . x – 4 . x = 0

$\Leftrightarrow$ x . (x – 4) = 0

$\Leftrightarrow$ x = 0 hoặc x – 4 = 0

$\Leftrightarrow$ x = 0 hoặc x = 4

Vậy x $\in$ {0; 4}.

b) (x – 3)² + 3 – x = 0

$\Leftrightarrow$ (x – 3)(x – 3) + ( –x + 3) = 0

$\Leftrightarrow$ (x – 3)(x – 3) – (x – 3) . 1 = 0

$\Leftrightarrow$ (x – 3)(x – 3 – 1) = 0

$\Leftrightarrow$ (x – 3)(x – 4) = 0

$\Leftrightarrow$ x – 3 = 0 hoặc x – 4 = 0

$\Leftrightarrow$ x = 3 hoặc x = 4

Vậy x $\in$ {3; 4}.

Bài 11. Với a³ + b³ + c³ = 3abc thì

A.
$a = b = c$ .
B.
$a + b + c = 1$ .
C.
$a = b = c$ hoặc $a + b + c = 0$ .
D.
$a = b = c$ hoặc $a + b + c = 1$ .

Đáp án : C

Phương pháp giải :

Sử dụng đẳng thức đặc biệt

a^{3} + b^{3} + c^{3} - 3 a b c = (a + b + c) (a^{2} + b^{2} + c^{2} - a b - b c - a c)

;

Lời giải chi tiết :

Từ đẳng thức đã cho suy ra $a^{3} + b^{3} + c^{3} - 3 a b c = 0$

$b^{3} + c^{3} = (b + c) (b^{2} + c^{2} - b c)$ $= (b + c) [{(b + c)}^{2} - 3 b c]$ $= {(b + c)}^{3} - 3 b c (b + c)$ $\Rightarrow a^{3} + b^{3} + c^{3} - 3 a b c = a^{3} + (b^{3} + c^{3}) - 3 a b c$ $= a^{3} + {(b + c)}^{3} - 3 b c (b + c) - 3 a b c$ $= (a + b + c) (a^{2} - a (b + c) + {(b + c)}^{2}) - [3 b c (b + c) + 3 a b c]$ $= (a + b + c) (a^{2} - a (b + c) + {(b + c)}^{2}) - 3 b c (a + b + c)$ $= (a + b + c) (a^{2} - a (b + c) + {(b + c)}^{2} - 3 b c)$ $= (a + b + c) (a^{2} - a b - a c + b^{2} + 2 b c + c^{2} - 3 b c)$ $= (a + b + c) (a^{2} + b^{2} + c^{2} - a b - a c - b c)$

Do đó nếu $a^{3} + (b^{3} + c^{3}) - 3 a b c = 0$ thì $a + b + c = 0$ hoặc $a^{2} + b^{2} + c^{2} - a b - a c - b c = 0$

Mà $a^{2} + b^{2} + c^{2} - a b - a c - b c = [{(a - b)}^{2} + {(a - c)}^{2} + {(b - c)}^{2}]$

Nếu ${(a - b)}^{2} + {(a - c)}^{2} + {(b - c)}^{2} = 0 \Leftrightarrow {\begin{array}{l} a - b = 0 \\ b - c = 0 \\ a - c = 0 \end{array} \Rightarrow a = b = c$

Vậy $a^{3} + (b^{3} + c^{3}) = 3 a b c$ thì $a = b = c$ hoặc $a + b + c = 0$ .

Bài 12. Gọi $x_{1}; x_{2}; x_{3}$ là các giá trị thỏa mãn $4 {(2 x - 5)}^{2} - 9 (4 x^{2} - 25)^{2} = 0$ . Khi đó $x_{1} + x_{2} + x_{3}$ bằng

A.
$- 3$ .
B.
$- 1$ .
C.
$\frac{- 5}{3}$ .
D.
$1$ .

Đáp án : D

Phương pháp giải :

Sử dụng hằng đẳng thức $a^{2} - b^{2} = (a - b) (a + b)$ để phân tích đa thức thành nhân tử.

Lời giải chi tiết :

$\begin{array}{l} 4 {(2 x - 5)}^{2} - 9 (4 x^{2} - 25)^{2} = 0 \\ \begin{array}{l} \Leftrightarrow 4 {(2 x - 5)}^{2} - 9 {[{(2 x)}^{2} - 5^{2}]}^{2} = 0 \\ \Leftrightarrow 4 {(2 x - 5)}^{2} - 9 {[(2 x - 5) (2 x + 5)]}^{2} = 0 \\ \Leftrightarrow 4 {(2 x - 5)}^{2} - 9 {(2 x - 5)}^{2} {(2 x + 5)}^{2} = 0 \\ \Leftrightarrow {(2 x - 5)}^{2} [4 - 9 {(2 x + 5)}^{2}] = 0 \\ \Leftrightarrow {(2 x - 5)}^{2} [4 - {(3 (2 x + 5))}^{2}] = 0 \\ \Leftrightarrow {(2 x - 5)}^{2} (2^{2} - {(6 x + 15)}^{2}) = 0 \\ \Leftrightarrow {(3 x - 5)}^{2} (2 + 6 x + 15) (2 - 6 x - 15) = 0 \\ \begin{array}{l} \Leftrightarrow {(3 x - 5)}^{2} (6 x + 17) (- 6 x - 13) = 0 \\ \Leftrightarrow [\begin{array}{l} x = \frac{5}{3} \\ x = \frac{- 17}{6} \\ x = \frac{13}{6} \end{array} \end{array} \end{array} \end{array}$

Suy ra $x_{1} + x_{2} + x_{3} = \frac{5}{3} - \frac{17}{6} + \frac{13}{6} = \frac{10 - 17 + 13}{6} = 1$

Bài 13. Cho biểu thức $A = 7^{19} + 7^{20} + 7^{21}$ . Khẳng định nào đúng cho biểu thức A.

A.
A không chia hết cho 7.
B.
A chia hết cho 2.
C.
A chia hết cho 57.
D.
A chia hết cho 114.

Đáp án : C

Phương pháp giải :

Phân tích biểu thức A thành nhân tử bằng phương pháp đặt nhân tử chung.

Lời giải chi tiết :

$\begin{array}{l} A = 7^{19} + 7^{20} + 7^{21} \\ = 7^{19} + 7^{19} .7 + 7^{19} {.7}^{2} \\ = 7^{19} . (1 + 7 + 7^{2}) \\ = 7^{19} .57 \end{array}$

Do $7^{19} ⋮ 7 \Rightarrow 7^{19} .57 ⋮ 7$ (A sai)

Ta có $7^{19}$ là số lẻ, 57 là số lẻ nên tích $7^{19} .57$ là số lẻ $\Rightarrow 7^{19} .57$ không chia hết cho 2. (B sai)

A chia hết cho 57. (C đúng)

A chia hết cho 57 nhưng A không chia hết cho 2 nên A không chia hết cho 57.2 = 114 (D sai)

B. Lý thuyết Phân tích đa thức thành nhân tử

1. Phương pháp đặt nhân tử chung

Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đã cho thành một tích của những đa thức. Mỗi đa thức này gọi là một nhân tử của đa thức đã cho.

Ví dụ 1. Phân tích đa thức A = 2x²y + 6xy² + 24xy thành nhân tử.

Hướng dẫn giải.

A = 2x²y + 6xy² + 24xy

= 2xy . x + 2xy . 3y + 2xy . 12

= 2xy(x + 3y + 12).

Ở Ví dụ 1, ta gọi đơn thức 2xy là nhân tử chung của các hạng tử của A, ta viết được A thành tích của 2xy với một đa thức. Cách làm như vậy gọi là phân tích đa thức A thành nhân tử bằng phương pháp đặt nhân tử chung.

Phương pháp đặt nhân tử chung

• Khi tất cả các số hạng của đa thức có một thừa số chung, ta sử dụng tính chất phân phối của phép nhân đối với phép cộng đưa thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.

• Các số hạng bên trong dấu () có được bằng cách lấy số hạng của đa thức chia cho

nhân tử chung.

2. Phương pháp sử dụng hằng đẳng thức

Tùy trường hợp ta có thể sử dụng những hằng đẳng thức khác nhau để phân tích một đa thức thành nhân tử.

Ví dụ 2. Phân tích các đa thức sau thành nhân tử:

a) 9x² – 12xy + 4y²;

b) 2x⁴ + 250xy³.

Hướng dẫn giải.

a) 9x² – 12xy + 4y² = (3x)² – 2 . 3x . 2y + (2y)² = (3x – 2y)²;

b) 2x⁴ + 250xy³ = 2x(x³ + 125y³) = 2x[x³ + (5y)³] = 2x(x + 5y)(x² – 5xy + y²).

=>Cách làm như Ví dụ 2 gọi là phân tích đa thức thành nhân tử bằng phương pháp sử dụng hằng đẳng thức.

Phương pháp sử dụng hằng đẳng thức

Dùng các hằng đẳng thức đáng nhớ để phân tích đa thức thành nhân tử.

=>Cần vận dụng linh hoạt các hằng đẳng thức để phù hợp với các nhân tử.

3. Phương pháp nhóm hạng tử

Ví dụ 3. Phân tích các đa thức sau thành nhân tử:

a) 2x² – 2y + 4xy – x;

b) x³ + 2x² + 6x + 5.

Hướng dẫn giải.

a) Cách 1:

2x² – 2y + 4xy – x

= (2x² + 4xy) – (x + 2y)

= 2x(x + 2y) – (x + 2y)

= (x + 2y)(2x – 1).

Cách 2:

2x² – 2y + 4xy – x

= (2x² – x) + (4xy – 2y)

= x(2x – 1) + 2y(2x – 1)

= (2x – 1)(x + 2y).

b) Cách 1:

x³ + 2x² + 6x + 5

= x³ + x² + x² + 5x + x + 5

= (x³ + x² + 5x) + (x² + x + 5)

= x(x² + x + 5) + (x² + x + 5)

= (x² + x + 5)(x + 1).

Cách 2:

x³ + 2x² + 6x + 5

= (x³ + 2x² + x) + (5x + 5)

= x(x² + 2x + 1) + 5(x + 1)

= x(x + 1)² + 5(x + 1)

= (x + 1)[x(x + 1) + 5]

= (x + 1)(x² + x + 5).

=>Cách làm như Ví dụ 3 gọi là phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử.

Phương pháp nhóm hạng tử

• Ta ghép các hạng tử của đa thức thành các nhóm để làm xuất hiện nhân tử chung.

• Tiếp theo, sử dụng phương pháp đặt nhân tử chung để phân tích đa cho thành nhân tử.

Chú ý:

+ Có thể sử dụng tính chất giao hoán và kết hợp để nhóm các số hạng của đa thức một cách linh hoạt (một đa thức có thể có nhiều cách nhóm hạng tử).

+ Khi phân tích đa thức thành nhân tử, ta phải phân tích triệt để đến khi không phân tích được nữa.

+ Khi nhóm các hạng tử của đa thức cần chú ý đến dấu của mỗi số hạng trong đa thức.

Video bài giảng Toán 8 Bài 9: Phân tích đa thức thành nhân tử - Kết nối tri thức

Đánh giá

1 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

162

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

132

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108 Lữ Ngọc My My

112

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

108

Tìm kiếm