Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Định lí Pythagore, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Định lí Pythagore. Mời các bạn đón xem:
Bài tập Toán 8 Định lí Pythagore
A. Bài tập Định lí Pythagore
Bài 1. Cho tam giác ABC vuông tại A, tính độ dài cạnh còn lại trong các trường hợp sau:
a) AB = 5 cm, AC = 12 cm;
b) ;
c) AB – AC = 7 cm, AB + AC = 17 cm.
Hướng dẫn giải
a) Do tam giác ABC vuông tại A nên áp dụng định lý Pythagore, ta có:
BC2 = AB2 + AC2
Suy ra BC2 = 52 + 122 = 25 + 144 = 169.
Do đó
Vậy BC = 13 cm.
b) Áp dụng định lý Pythagore vào tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
Suy ra
Do đó
Vậy AC = 11,87 cm.
c) Theo bài ta có: AB – AC = 7 suy ra AB = AC + 7
Mặt khác, AB + AC = 17 suy ra AC + 7 + AC = 17
Hay 2AC = 17 – 7 = 10 suy ra AC = 5 cm và AB = 12 cm
Do tam giác ABC vuông tại A nên áp dụng định lý Pythagore, ta có:
BC2 = AB2 + AC2
Suy ra BC2 = 52 + 122 = 25 + 144 = 169.
Do đó .
Vậy BC = 13 cm.
Bài 2. Cho tam giác ABC vuông tại A. Biết và BC = 20 cm. Tính độ dài các cạnh AB và AC.
Hướng dẫn giải
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A, ta có:
AB2 + AC2 = BC2 = 202 = 400.
Từ đề bài: hay suy ra .
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
AB2 = 16.16 suy ra AB = 16 cm.
AC2 = 9 . 16 = 144 suy ra AC = 12 cm.
Vậy AB = 16 cm; AC = 12 cm.
Bài 3. Cho hình vẽ sau. Tìm giá trị của a.
Hướng dẫn giải
Áp dụng định lý Pythagore và tam giác ADE vuông tại A, ta có:
AD2 + AE2 = DE2
AE2 = DE2 – AD2
Suy ra AE = 4.
Suy ra AB = AE + EB = 4 + 4 = 8.
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A, ta có:
AB2 + AC2 = BC2
Suy ra BC2 = 82 + 62 = 100 suy ra BC = 10 hay a = 10.
Vậy a = 10.
Bài 4. Cho tam giác ABC vuông tại A.
a) Tính độ dài cạnh AB nếu biết BC = 20 dm, AC = 12 dm.
b) Tính độ dài cạnh AC nếu biết BC = 8 m, AB = m.
c) Tính độ dài cạnh BC nếu biết AB = 12 cm, AC = 9 cm.
Hướng dẫn giải
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
a) AB2 = BC2 – AC2 = 202 – 122 = 400 – 144 = 256 = 162.
Vậy cạnh AB dài 16 dm.
b) AC2 = BC2 – AB2 = 82 – = 64 – 15 = 49 = 72.
Vậy cạnh AC dài 7 m.
c) BC2 = AB2 + AC2 = 122 + 92 = 144 + 81 = 225 = 152.
Vậy cạnh BC dài 15 cm.
Bài 5. Chứng minh tam giác ABC vuông trong các trường hợp sau:
a) AB = 10 cm, AC = 8 cm, BC = 6 cm.
b) AB = 8 dm, AC = 15 dm, BC = 17 dm.
Hướng dẫn giải
a) Ta có: 102 = 82 + 62, suy ra AB2 = AC2 + BC2.
Vậy tam giác ABC là tam giác vuông tại C.
b) Ta có: 172 = 82 + 152, suy ra BC2 = AB2 + AC2
Vậy tam giác ABC là tam giác vuông tại A.
Bài 6. Hình dưới mô tả một cánh buồm có dạng tam giác vuông, được buộc vào cột buồm thẳng đứng, với độ dài hai cạnh góc vuông là 12 m và 5 m (hình vẽ).
a) Tính độ dài cạnh huyền của cánh buồm.
b) Vật liệu dùng để làm cánh buồm là vải. Tính diện tích vải dùng để làm một cánh buồm như vậy.
Hướng dẫn giải
a) Gọi x là độ dài cạnh huyền của cánh buồm.
Áp dụng định lí Pythagore cho tam giác vuông, ta có:
x2 = 122 + 52 = 144 + 25 = 169 = 132
Vậy độ dài cạnh huyền của cánh buồm là 13 m.
b) Diện tích vải dùng để làm cánh buồm đó là: = 30 (m2).
Bài 7.
Chọn phát biểu đúng nhất về định lí Pythagore:
Hướng dẫn giải
Đáp án : A
Bài 8.
Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB = AC = 2 dm
Hướng dẫn giải
Đáp án : D
Tam giác ABC vuông cân ở A nên theo định lý Pythagore ta có mà
AB = AC = 2 dm
Nên
Bài 9. Cho hình vẽ. Tính x.
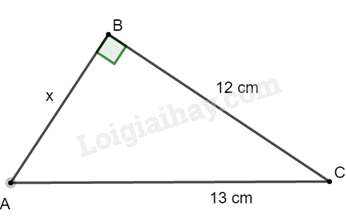
Hướng dẫn giải
Đáp án : D
Áp dụng định lí Pythagore cho tam giác ABC vuông tại B ta được :
Vậy x = 5 cm
B. Lý thuyết Định lí Pythagore
1. Định lí Pythagore
Định lí Pythagore:
Trong một tam giác vuông, bình phương độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.
|
GT |
∆ABC, |
|
KL |
BC2 = AB2 + AC2 |
Ví dụ 1.
a) Cho một hình tam giác vuông có hai cạnh góc vuông là a = 5 cm, b = 6 cm. Tính độ dài cạnh huyền của tam giác vuông đó.
b) Cho tam giác vuông DEF có cạnh huyền EF = 5 cm và cạnh DE = 4 cm. Tính độ dài cạnh DF.
Hướng dẫn giải
a) Gọi c là độ dài cạnh huyền của tam giác vuông đã cho. Áp dụng định lí Pythagore, ta có:
c2 = a2 + b2 = 52 + 62 = 25 + 36 = 61.
Vậy độ dài cạnh huyền của tam giác đó là c = cm.
b)
Áp dụng định lí Pythagore vào tam giác vuông DEF có cạnh huyền EF, ta có:
EF2 = DE2 + DF2
Suy ra DF2 = EF2 – DE2 = 52 – 42 = 25 – 16 = 9 = 32.
Vậy cạnh DF dài 3 cm.
2. Định lí Pythagore đảo
Định lí Pythagore đảo:
Nếu một tam giác có bình phương độ dài của một cạnh bằng tổng các bình phương độ dài của hai cạnh kia thì tam giác đó là tam giác vuông.
|
GT |
∆ABC, BC2 = AB2 + AC2 |
|
KL |
Ví dụ 2. Các tam giác sau có phải là tam giác vuông không?
a) Tam giác ABC có AB = 6 m, BC = 8 m, AC = 10 m.
b) Tam giác DEF có DE = 4 dm, DF = 10 dm, EF = 6 dm.
Hướng dẫn giải
a) Ta có: 102 = 62 + 82, suy ra AC2 = AB2 + BC2.
Vậy tam giác ABC vuông tại B.
b) Ta có DF là cạnh dài nhất và 102 ≠ 42 + 62, suy ra DF2 ≠ DE2 + EF2.
Vậy tam giác DEF không phải là tam giác vuông.
3. Vận dụng định lí Pythagore
Ta có thể vận dụng định lí Pythagore để tính nhiều yếu tố khoa học và đời sống như tính độ dài đoạn thẳng, khoảng cách giữa hai điểm, chiều dài, chiều cao của vật, …
Ví dụ 3. Một cái thang dài 5 m đang dựa vào một bức tường, chân thang cách chân tường 3 m (hình vẽ). Tính chiều cao mà thang có thể vươn tới.
Hướng dẫn giải
Gọi AC là khoảng cách từ chân thang đến chân tường; BC là độ dài của thang và AB là chiều cao thang có thể vươn tới.
Ta được tam giác vuông ABC như hình dưới.
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
Suy ra AB2 = BC2 – AC2 = 52 – 32 = 25 – 9 = 16 = 42.
Vậy chiều cao mà thang có thể vươn tới là AB = 4 m.
Video bài giảng Toán 8 Bài 1: Định lí Pythagore - Chân trời sáng tạo