Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Vật lí gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Vật lí. Mời các bạn đón xem:

Top 1000 câu hỏi thường gặp môn Vật lí (Phần 10)

Bài 25: Hai quả cầu nhỏ bằng kim loại giống hệt nhau được treo ở hai đầu dây có cùng chiều dài. Hai đầu kia của hai dây móc vào cùng một điểm. Cho hai quả cầu tích điện bằng nhau, lúc cân bằng chúng cách nhau R = 6,35 cm. Chạm tay vào một trong hai quả cầu, hãy tính khoảng cách R giữa hai quả cầu sau khi chúng đạt vị trí cân bằng mới. Giả thiết chiều dài mỗi dây khá lớn so với khoảng cách hai quả cầu lúc cân bằng. Lấy \[\sqrt[3]{4} = 1,5785\].

A. 2 cm.

B. 3 cm.

C. 6 cm.

D. 4 cm.

Lời giải:

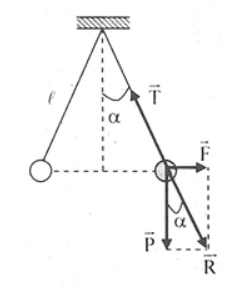
Các lực tác dụng lên mỗi quả cầu gồm: trọng lực \[\overrightarrow P \], lực tương tác tĩnh điện \[{\overrightarrow F _d}\] và lực căng của dây treo \[\overrightarrow T \].

Khi quả cầu cân bằng thì: \[\underbrace {\overrightarrow P  + {{\overrightarrow F }_d}}_{\overrightarrow R } + \overrightarrow T  = \overrightarrow 0  \Leftrightarrow \overrightarrow R  + \overrightarrow T  = \overrightarrow 0 \]

\[ \Rightarrow \overrightarrow R \] có phương sợi dây \[ \Rightarrow \tan \alpha  = \frac{F}{P} \Rightarrow F = P.\tan \alpha  = P\frac{{\frac{R}{2}}}{{\sqrt {{\ell ^2} - {{\left( {\frac{R}{2}} \right)}^2}} }}\]

Nhận thấy:

\[{\ell ^2} >  > {\left( {\frac{R}{2}} \right)^2} \Rightarrow {\ell ^2} - {\left( {\frac{R}{2}} \right)^2} \approx {\ell ^2} \Rightarrow \sqrt {{\ell ^2} - {{\left( {\frac{R}{2}} \right)}^2}}  \approx \ell  \Rightarrow F \approx \frac{{PR}}{{2\ell }}\]

Lúc đầu: \[{F_1} = k\frac{{{q^2}}}{{{R^2}}} = \frac{{PR}}{{2\ell }}\,\,\,\,\left( 1 \right)\]

Giả sử ta chạm tay vào quả cầu 1, kết quả sau đó quả cầu 1 sẽ mất điện tích, lúc đó giữa hai quả cầu không còn lực tương tác nên chính sẽ trở về vị trí dây thẳng đứng. Khi chúng vừa chạm nhau thì điện tích của quả 2 sẽ truyền sang cho quả 1 và lúc này điện tích mỗi quả sẽ là:

\[{q_1}' = {q_2}' = \frac{{{q_2}}}{2} = \frac{q}{2} \Rightarrow {F_2} = k\frac{{{q^2}}}{{4{{\left( {R'} \right)}^2}}} = \frac{{PR'}}{{2\ell }}\,\,\,\left( 2 \right)\]

Từ (1) và (2) ta có: \[4{\left( {R'} \right)^3} = {R^3} \Rightarrow R' = \frac{R}{{\sqrt[3]{4}}} \approx 4\,cm\]