Đề thi vào lớp 10 môn Toán chuyên Hùng Vương năm 2009-2010
Chỉ 100k mua trọn bộ Đề thi vào lớp 10 môn Toán chuyên Hùng Vương năm 2009-2010 có lời giải chi tiết (chỉ 20k cho 1 đề thi bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Sở Giáo dục và Đào tạo .....
Kì thi tuyển sinh vào lớp 10 THPT chuyên
Đề thi môn: Toán
Năm học: ......
Thời gian: 150 phút (không kể thời gian giao đề)
Câu 1 (2 điểm): Cho hệ phương trình: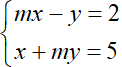 
(m là tham số)
a) Chứng tỏ hệ đã cho luôn có nghiệm duy nhất với mọi m.
b) Tìm giá trị của m để hệ phương trình trên có nghiệm (x, y) thoả mãn x + y = 5.
Câu 2 (1 điểm): Tìm tất cả các số nguyên dương x,y,z thỏa mãn x3-y3=z2 trong đó y là số nguyên tố, (z;3)=(z;y)=1
Câu 3 (3 điểm):
a) Giải phương trình: (x+1)2009+(x+1)2008(x+2)+(x+1)2007(x+2)2+...(x+1)(x+2)2008+(x+2)2009=0
b) Cho x,y là các số thực dương thoả mãn điều kiện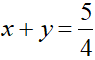 
. Tìm giá trị nhỏ nhất của biểu thức 
Câu 4 (3 điểm): Cho tam giác ABC có ba góc nhọn, nội tiếp trong đường tròn (O) và điểm P nằm trong tam giác ABC sao cho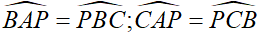 
. Đường thẳng AP cắt cạnh BC tại M
a) Chứng minh rằng M là trung điểm của cạnh BC .
b) Chứng minh rằng tứ giác BHPC nội tiếp trong một đường tròn (ω) , trong đó H là trực tâm tam giác .
c) Đường trung trực của đoạn thẳng PA cắt đường thẳng BC tại Q . Chứng minh rằng QA tiếp xúc với (O) và QP tiếp xúc với (ω) .
Câu 5 (1 điểm):Cho các số thực không âm a,b,c thỏa mãn ab+bc+ca=3. Chứng minh rằng:
Xem thêm các đề thi vào lớp 10 môn Toán chuyên hay khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
