Tailieumoi.vn giới thiệu Giải sách bài tập Toán lớp 9 Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Phương pháp giải:
Sử dụng:
- Diện tích xung quanh của hình nón: .
- Thể tích hình nón: .
( là bán kính đường tròn đáy, là đường sinh, là chiều cao)..
Lời giải:
Khi quay tam giác vuông một vòng xung quanh cạnh huyền ta thu được hai hình nón có đáy úp vào nhau, bán kính đường tròn đáy bằng đường cao kẻ từ đến cạnh huyền .
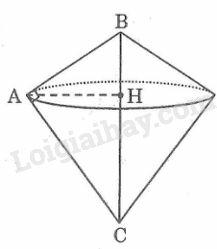
Trong tam giác vuông ta có:
+)
+)
+) (hệ thức lượng trong tam giác vuông)
Diện tích xung quanh hình tạo thành là:
(đơn vị diện tích)
Thể tích hình tạo thành là:
.
Phương pháp giải:
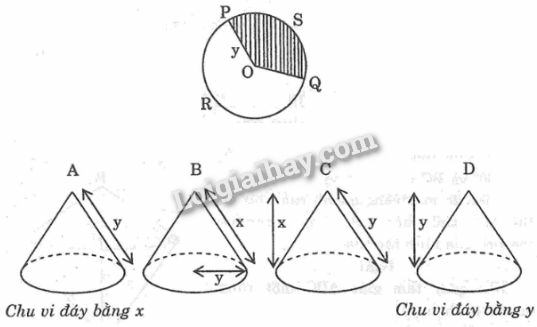
Quan sát hình vẽ để tưởng tượng hình nón tạo thành từ phần hình quạt còn lại sau khi cắt.
Lời giải:
Phần còn lại ghép thành hình nón sẽ có đường sinh là ; chu vi đáy là độ dài của là .
Chọn hình A.
Cụ Bá uống một lượng rượu nên “chiều cao” của rượu còn lại trong cốc bằng một nửa chiều cao ban đầu.
Hỏi cụ Bá đã uống bao nhiêu phần rượu trong cốc?
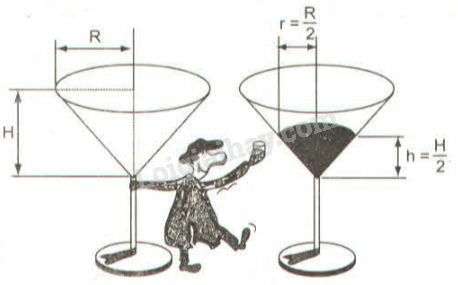
Phương pháp giải:
Sử dụng:
- Thể tích hình nón: .
( là bán kính đường tròn đáy, là chiều cao).
Lời giải:
Thể tích rượu ban đầu trong cốc là:
Thể tích rượu còn lại trong cốc là:
Thể tích rượu đã uống là:
Vậy cụ Bá đã uống thể tích rượu trong cốc.
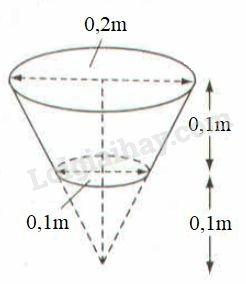
Thể tích nước chứa đầy xô sẽ là (tính theo ):
(A) ; (B) ;
(C) ; (D) .
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
- Thể tích hình nón: .
( là bán kính đường tròn đáy, là chiều cao).
Lời giải:
Thể tích hình nón có đường kính đáy là:
Thể tích hình nón có đường kính đáy là:
Thể tích nước chứa đầy xô là:
Chọn (B).
(A) ; (B) ;
(C) ; (D) .
(Chọn và tính gần đúng đến ).
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
- Diện tích xung quanh của hình nón: .
- Diện tích toàn phần của hình nón: .
( là bán kính đường tròn đáy, là đường sinh).
Lời giải:
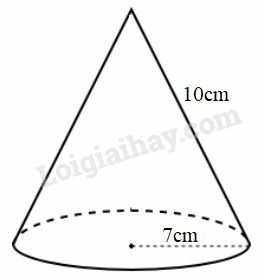
Diện tích xung quanh hình nón là:
Diện tích đáy hình nón là:
.
Chọn (D).
a) Tính diện tích toàn phần của hình tạo thành khi quay hình bình hành đúng một vòng quanh cạnh và diện tích toàn phần của hình tạo thành khi quay quanh cạnh .
b) Xác định giá trị khi và .
Phương pháp giải:
Sử dụng:
- Diện tích xung quanh của hình nón: .
( là bán kính đường tròn đáy, là đường sinh).
- Diện tích xung quanh hình trụ: .
( là bán kính đường tròn đáy, là chiều cao).
Lời giải:
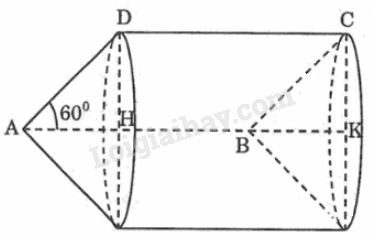
a) Khi quay hình bình hành một vòng quanh cạnh thì cạnh và vạch nên hình nón bằng nhau có đường sinh cạnh vạch nên hình trụ có bán kính đáy bằng bán kính đáy hình nón.
Trong có , ta có:
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh hình nón và diện tích xung quanh hình trụ:
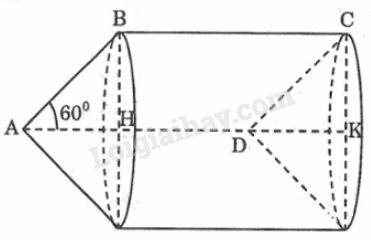
Khi quay hình bình hành quanh trục một vòng thì cạnh và vạch nên hai hình nón bằng nhau có đường sinh Cạnh vạch nên hình trụ có bán kính đáy bằng bán kính đáy hình nón.
Bán kính đáy:
là diện tích toàn phần hình tạo thành bằng tổng diện tích xung quanh hai hình nón cộng với diện tích hình trụ.
b) Để
Vì
Vậy thì .
Để
Vì
.
Vậy thì .
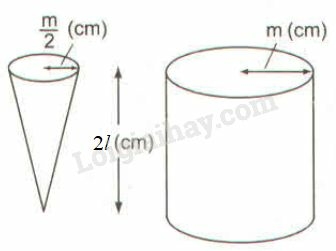
Người ta múc đầy nước vào hình nón và đổ vào hình trụ (không chứa gì cả) thì độ cao của nước trong hình trụ là:
(A) (cm); (B) ;
(C) (cm); (D) (cm).
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
- Thể tích hình nón: .
( là bán kính đường tròn đáy, là chiều cao).
- Thể tích hình trụ: .
( là bán kính đường tròn đáy, là chiều cao, là diện tích đáy).
Lời giải:
Thể tích hình nón là:
Thể tích hình trụ là:
Vậy khi đổ đầy nước vào hình nón rồi đổ vào hình trụ thì độ cao của nước trong hình trụ là ().
Chọn (A).
(A) (B)
(C) (D)
Phương pháp giải:
Sử dụng:
- Thể tích hình nón: .
( là bán kính đường tròn đáy, là chiều cao).
Lời giải:
Gọi bán kính đáy hình nón ban đầu là , độ dài đường cao là .
Thể tích hình nón ban đầu là:
Thể tích nón mới khi bán kính và chiều cao tăng là:
Chọn (D).
Sử dụng:
- Công thức tính thể tích hình trụ: .
( là bán kính đường tròn đáy, là chiều cao, là diện tích đáy).
Lời giải:
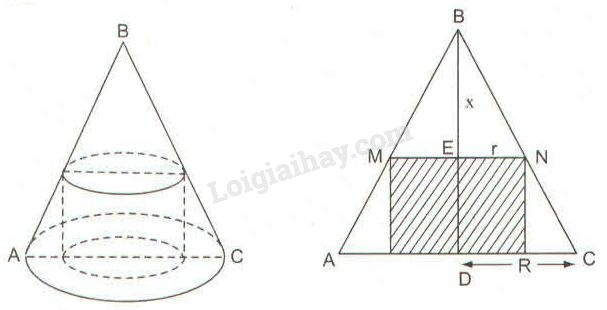
Gọi bán kính đáy hình nón là , chiều cao hình nón là , bán kính đáy hình trụ là , chiều cao phần hình nón cắt đi là .
Vì , theo hệ quả định lí Ta-lét ta có:
hay
Thể tích hình trụ là:
Phần bỏ đi của hình nón ít nhất có nghĩa là thể tích của hình trụ lớn nhất:
)
Vì là các hằng số nên thể tích hình trụ lớn nhất khi và chỉ khi lớn nhất. Ta có
Áp dụng bất đẳng thức Cô - si cho ba số dương ta có:
Dấu "=" xảy ra khi
Vậy khi phần cắt bỏ ở phía trên hình nón có chiều cao bằng chiều cao hình nón thì phần bỏ đi là ít nhất.
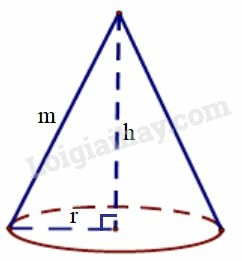
Chiều cao là , bán kính đường tròn đáy là và độ dài đường sinh thì thể tích hình nón này là:
(A)
(B)
(C)
(D)
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
- Thể tích hình nón: .
( là bán kính đường tròn đáy, là chiều cao).
Lời giải:
Chiều cao hình nón là , bán kính đường tròn đáy là , độ dài đường sinh là
Thể tích hình nón là:
Chọn (B).
(A) ; (B) ;
(C) ; (D)
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
- Thể tích hình trụ: .
( là bán kính đường tròn đáy, là chiều cao).
- Thể tích hình nón: .
( là bán kính đường tròn đáy, là chiều cao).
Lời giải:
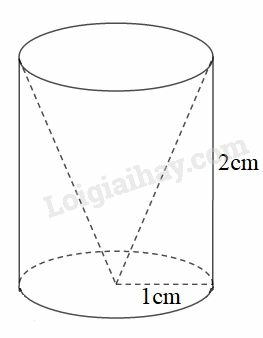
Thể tích hình trụ là:
Thể tích hình nón là:
Thể tích phần còn lại của hình trụ là:
Chọn (B).
Phương pháp giải:
Sử dụng:
- Thể tích hình nón: .
( là bán kính đường tròn đáy, là chiều cao).
- Định lí Pytago trong tam giác vuông: Bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông.
Lời giải:
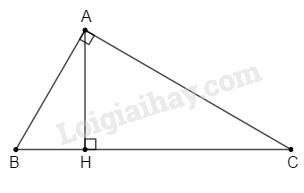
có , đặt ; là đường cao kẻ từ đỉnh đến cạnh huyền .
Ta có: (hệ thức lượng trong tam giác vuông)
- Khi quay tam giác vuông quanh cạnh huyền một vòng thì cạnh và vạch nên hai hình nón có chung đáy có bán kính đáy bằng đường cao và tổng chiều cao hình nón bằng cạnh huyền Như vậy, thể tích hình sinh ra là:
(1)
- Khi quay quanh cạnh một vòng ta thu được hình nón có chiều cao , bán kính đáy và thể tích hình sinh ra là:
- Khi quay quanh cạnh một vòng ta thu được hình nón có chiều cao , bán kính đáy và thể tích hình sinh ra là:
Ta có:
Áp dụng định lí Pytago vào vuông tại , ta có:
(2)
Từ (1) và (2) suy ra: .
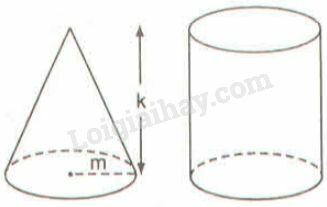
Chứa đầy cát vào hình nón rồi đổ hết vào hình trụ thì độ cao của cát trong hình trụ sẽ là:
(A) (B)
(C) (D)
Hãy chọn kết quả đúng.
Phương pháp giải:
Sử dụng:
- Thể tích hình nón: .
( là bán kính đường tròn đáy, là chiều cao).
- Thể tích hình trụ: .
( là bán kính đường tròn đáy, là chiều cao, là diện tích đáy).
Lời giải:
Chứa đầy cát vào hình nón rồi đổ hết vào hình trụ thì độ cao của cát trong hình trụ sẽ bằng độ cao của hình trụ tức là
Chọn (B).