Đề thi vào lớp 10 môn Toán chuyên Bình Phước
Chỉ 100k mua trọn bộ Đề thi vào lớp 10 môn Toán chuyên Bình Phước có lời giải chi tiết (chỉ 20k cho 1 đề thi bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Sở Giáo dục và Đào tạo .....
Kì thi tuyển sinh vào lớp 10 THPT chuyên
Đề thi môn: Toán
Năm học: ......
Thời gian: 150 phút (không kể thời gian giao đề)
Câu 1 : Cho biểu thức: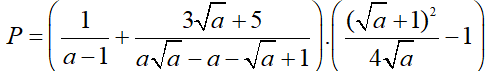 
với a>0, a≠1
a) Rút gọn P
b) Đặt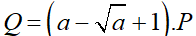 
. Chứng minh rằng Q>1
Câu 2 :
Cho phương trình: x2-2(m+1)x+m2=0. Tìm m để pt có 2 nghiệm x1, x2 thỏa mãn (x1-m)2+x2=m+2
Câu 3 :
a) Giải phương trình: 
b) Giải hệ phương trình: 
Câu 4 : Giải phương trình trên tập số nguyên: 
Câu 5 : Cho tam giác ABC nhọn (AB<AC) nội tiếp trong đường tròn tâm O, bán kính R. Gọi H là trực tâm của tam giác ABC . Gọi M là trung điểm của BC.
a) Chứng minh rằng: AH=2.OM
b) Dựng hình bình hành AHIO . Gọi J là tâm Đường tròn ngoại tiếp tam giác OBC. Chứng minh rằng: OI.OJ=R2
c) Gọi N là giao điểm của AH và đường tròn tâm O (N khác A). Gọi D là điểm bất kỳ trên cung nhỏ NC của đường tròn tâm O (D kác N và C ). Gọi E là điểm đối xứng với D qua AC, K là giao điểm của AC và HE. Chứng minh rằng: 
Câu 6 :
a) Cho a,b là các số thực dương. Chứng minh rằng: 
b) Cho a,b là các số thực dương thỏa mãn a+b=ab . Tìm giá trị nhỏ nhất của biểu thức: 
Xem thêm các đề thi vào lớp 10 môn Toán chuyên hay khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
