Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 2: Đường thẳng trong mặt phẳng tọa độ chi tiết sách Toán 10 Tập 2 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 2: Đường thẳng trong mặt phẳng tọa độ
1. Phương trình đường thẳng
Giải toán lớp 10 trang 46 Tập 2 Chân trời sáng tạo
Khởi động trang 46 Toán lớp 10:
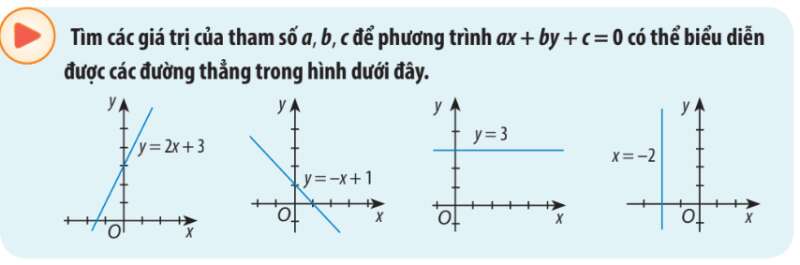
Lời giải:
+) Hình 1:
Vậy
+) Hình 2:
Vậy
+) Hình 3:
Vậy
+ Hình 4:
Vậy
a) Tính tích vô hướng và nêu nhận xét về phương của hai vectơ
b) Gọi là điểm di động trên . Chứng tỏ rằng vectơ luôn cùng phương với vectơ và luôn vuông góc với vectơ
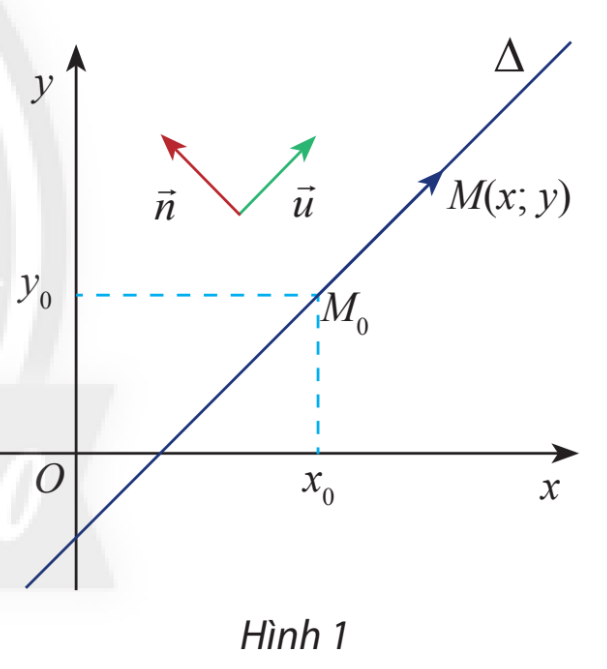
Phương pháp giải:
a) +) Áp dụng ứng dụng biểu thức tọa độ của vectơ tính tích vô hướng
+) Dựa vào kết quả tích vô hướng các định phương (bằng 0 thì vuông góc)
b) +) Xác định tỉ lệ giũa các tọa độ của hai vectơ để so sánh về phương
+) Tính tích vô hướng để chứng minh vuông góc
Lời giải:
a) Ta có
Tích vô hướng bằng 0 nên hai vectơ có phương vuông góc với nhau
b) Vectơ có giá là đường thẳng
=> luôn cùng phương với vectơ
=> vectơ có phương vuông góc với vectơ
Giải toán lớp 10 trang 47 Tập 2 Chân trời sáng tạo
Phương pháp giải:
M và thuộc nên làm vectơ chỉ phương
Lời giải:
mà nhận làm vectơ chỉ phương nên ta có:
Vậy
b) Tìm tọa độ điểm P trên ,biết P có tung độ bằng 1.
Lời giải:
a) Phương trình tham số của đường thẳng
b) Thay vào phương trình ta được
Thay vào phương trình , ta được
Vậy
Giải toán lớp 10 trang 48 Tập 2 Chân trời sáng tạo
a) Viết phương trình tham số của đường thẳng d biểu diễn đường đi của ô tô
b) Tìm tọa độ của xe tương ứng với t = 2; t = 4
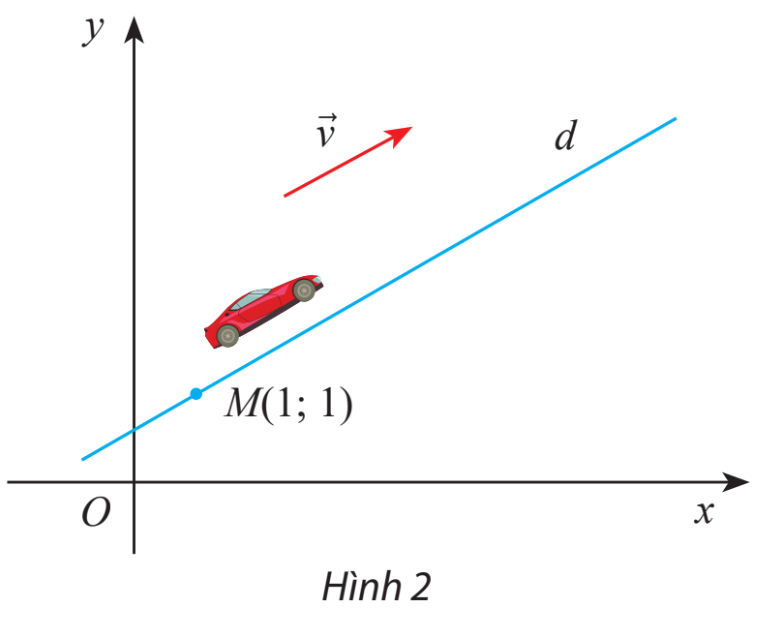
Lời giải:
a) Phương trình tham số của đường thẳng
b) Thay vào phương trình ta được
Vậy khi thì tọa độ của ô tô là
Thay vào phương trình ta được
Vậy khi thì tọa độ của ô tô là
(với )
Phương pháp giải:
Bước 1: Tìm tọa độ điểm M qua và a,b
Bước 2: Thay vào phương trình
Lời giải:
nhận vectơ làm vectơ pháp tuyến, suy ra vectơ chỉ phương của là
M và thuộc đường thẳng nên nhận làm vectơ chỉ phương
, suy ra
Suy ra
Thay tọa độ điểm M vào phương trình ta có:
(đúng vì )
Vậy thỏa mãn phương trình đã cho
Giải toán lớp 10 trang 49 Tập 2 Chân trời sáng tạo
a) Đường thẳng đi qua điểm và có vectơ pháp tuyến
b) Đường thẳng đi qua gốc tọa độ và có vectơ chỉ phương
c) Đường thẳng đi qua hai điểm
Lời giải:
a) Đường thẳng có vectơ pháp tuyến nên có vectơ chỉ phương , nên ta có phương trình tham số của là :
Đường thẳng đi qua điểm và có vectơ pháp tuyến
Phương trình tổng quát của đường thẳng d là:
b) Đường thẳng đi qua gốc tọa độ và có vectơ chỉ phương , nên có phương trình tham số là:
Đường thẳng có vectơ chỉ phương ,nên có vectơ pháp tuyền là và đi qua
Ta có phương trình tổng quát là
c) Đường thẳng đi qua hai điểm nên có vectơ chỉ phương và có vectơ pháp tuyến
Phương trình tham số của là:
Phương trình tổng quát của là:
a) Viết phương trình tổng quát của đường thẳng biểu diễn đường đi của điểm M
b) Tìm tọa độ của điểm M khi cắt trục hoành
Phương pháp giải:
a) Từ vectơ chỉ phương tìm vectơ pháp tuyến và viết phương trình tổng quát
VTCP (a;b) => VTPT: (-b; a) hoặc (b; -a)
b) M thuộc trục hoành thì M có tọa độ (m; 0)
Lời giải:
a) Đường thẳng có vectơ chỉ phương ,nên có vectơ pháp tuyền là và đi qua
Ta có phương trình tổng quát là
b) Điểm M thuộc trục hoành nên tung độ bằng 0
Thay vào phương trình ta tìm được
Vậy cắt trục hoành tại điểm
Giải toán lớp 10 trang 51 Tập 2 Chân trời sáng tạo
Lời giải:
a) Ta có
Vậy hàm số bậc ứng với đường thẳng là
b) Ta có
Vậy hàm số bậc ứng với đường thẳng là
c) Ta có
Vậy hàm số bậc ứng với đường thẳng là
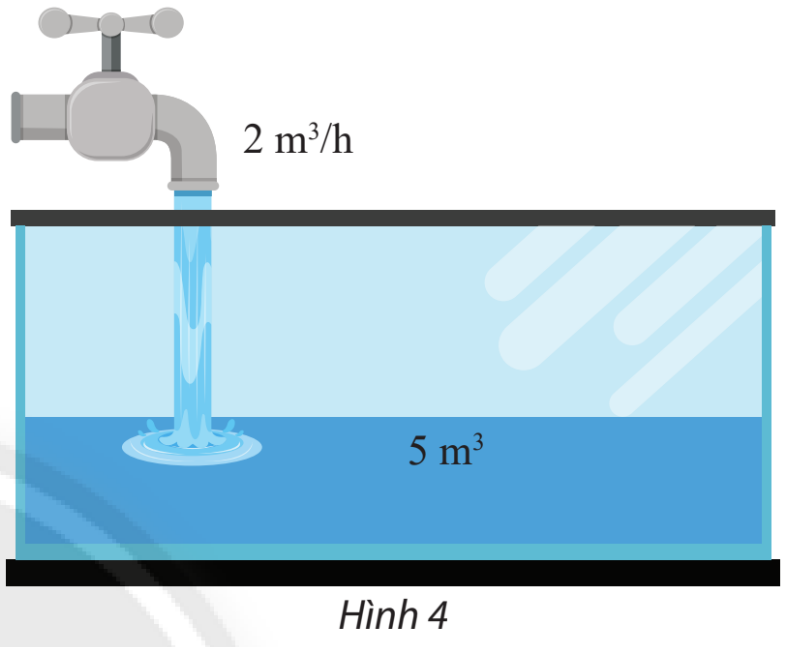
a) Viết biểu thức tính thể tích y của nước có trong bể sau x giờ
b) Gọi là hàm số xác định được từ câu a). Vẽ đồ thị d của hàm số này
c) Viết phương trình tham số và phương trình tổng quát của đường thẳng d
Lời giải:
a) Thể tích nước trong bể được tính bằng công thức
b)
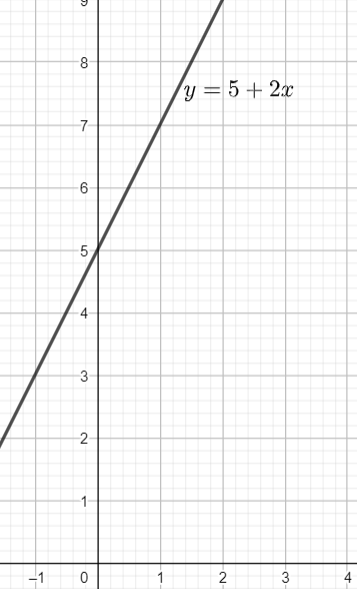
c) Ta có đồ thị hàm số bậc nhất
Vậy phương trình tổng quát của đường thẳng d là
Từ phương trình tổng quát ta có vectơ pháp tuyến , từ đó ta có vectơ chỉ phương
Khi thì nên đường thẳng đó đi qua điểm
Ta có phương trình tham số của đường thẳng d là
2. Vị trí tương đương đối của hai đường thẳng
Khám phá 4 trang 51 Toán lớp 10: Cho hai đường thẳng và một vectơ pháp tuyến lần lượt là và
Nêu nhận xét về vị trí tương đối giữa và trong các trường hợp sau:
a) và cùng phương (hình 5a,b)
b) và không cùng phương (hình 5c,d)
c) và vuông góc (hình 5d)
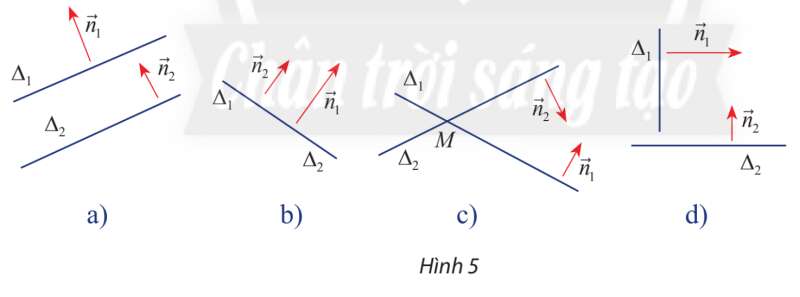
Lời giải:
Dựa vào hình vẽ ta có
a) và cùng phương thì hai đường thẳng và song song
b) và không cùng phương thì hai đường thẳng và cắt nhau
c) và vuông góc thì hai đường thẳng và vuông góc
Giải toán lớp 10 trang 53 Tập 2 Chân trời sáng tạo
a) và
b) và
c) và
Phương pháp giải:
Bước 1: Xác định cặp vectơ pháp tuyến (hoặc chỉ phương) của hai đường thẳng
Bước 2:
+) Nếu 2 vecto cùng phương: Lấy điểm A thuộc d1. Kiểm tra A có thuộc d2 hay không.
=> KL: 2 đường thẳng song song nếu A không thuộc d2.
2 đường thẳng trùng nhau nếu A thuộc d2.
+) Nếu 2 vecto không cùng phương: Tính tích vô hướng
Nếu bằng 0 thì hai đường thẳng vuông góc, nếu khác 0 thì 2 đường thẳng chỉ cắt nhau.
=> Giải hệ phương trình từ hai đường thẳng để tìm giao điểm
Lời giải:
a) và có vectơ pháp tuyến lần lượt là
Ta có nên
Giải hệ phương trình ta được nghiệm
Suy ra hai đường thẳng và vuông góc và cắt nhau tại
b) và có vectơ pháp tuyến lần lượt là
trùng nhau nên hai vectơ pháp tuyến cùng phương. Suy ra và song song hoặc trùng nhau
Lấy điểm thuộc , thay tọa độ của A vào phương trình , ta được , suy ra A không thuộc đường thẳng
Vậy hai đường thẳng và song song
c) và có vectơ pháp tuyến lần lượt là
Ta có suy ra hai vectơ pháp tuyến cùng phương. Suy ra và song song hoặc trùng nhau
Lấy điểm thuộc , thay tọa độ của A vào phương trình , ta được , suy ra A thuộc đường thẳng
Vậy hai đường thẳng và trùng nhau
Vận dụng 4 trang 53 Toán lớp 10: Viết phương trình đường thẳng :
a) Đi qua điểm và song song với đường thẳng
b) Đi qua điểm và vuông góc với đường thẳng
Phương pháp giải:
Bước 1: Từ đường thẳng đã cho xác định vectơ pháp tuyến hoặc vectơ chỉ phương
Bước 2: Viết phương trình tổng quát hoặc phương trình tham số
Lời giải:
a) song song với đường thẳng nên nhận vectơ pháp tuyến của đường thẳng làm vectơ pháp tuyến là
đi qua điểm nên ta có phương trình tổng quát
b) vuông góc với đường thẳng nên nhận vectơ pháp tuyến của đường thẳng làm vectơ chỉ phương là
đi qua điểm nên ta có phương trình tham số:
3. Góc giữa hai đường thẳng
Giải toán lớp 10 trang 54 Tập 2 Chân trời sáng tạo
Khám phá 5 trang 54 Toán lớp 10: Cho hai đường thẳng xy và zt cắt nhau tại O và cho biết (hình 6)
Tính số đo các góc và
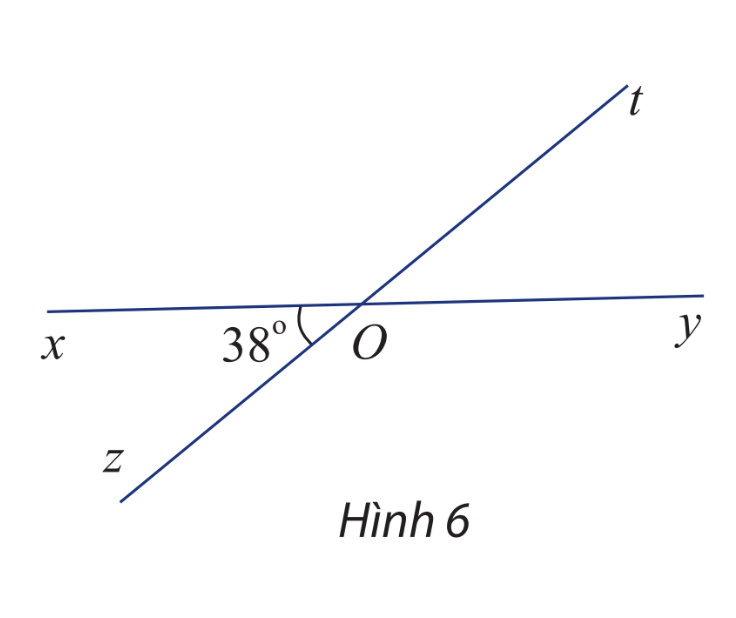
Lời giải:
Ta có hai góc và đối đỉnh nên
hai góc và đối đỉnh nên
và bù nhau nên
Vậy và
Khám phá 6 trang 54 Toán lớp 10: Cho hai đường thẳng
() và
có vectơ pháp tuyến lần lượt là và .
Tìm tọa độ và tính
Phương pháp giải:
+) Tọa độ của được xác định từ pjuowng trình tổng quát của hai đường thẳng
+) Áp dụng biểu thức tọa độ của vectơ trong mặt phẳng
Lời giải:
+) Từ phương trình ta xác định được tọa độ của vectơ là
+) Từ phương trình ta xác định được tọa độ của vectơ là
+)
Giải toán lớp 10 trang 56 Tập 2 Chân trời sáng tạo
Thực hành 5 trang 56 Toán lớp 10: Tìm số đo của góc giữa hai đường thẳng và trong các trường hợp sau
a) và
b) và
c) và
Phương pháp giải:
Bước 1: Xác định vectơ pháp tuyến của hai đường thẳng đã cho
Bước 2: Tính số đo góc giữa hai đường thẳng bằng công thức
Lời giải:
a) Ta có vectơ pháp tuyến của hai đường thẳng và lần lượt là
Ta có
b) Ta có vectơ pháp tuyến của hai đường thẳng và lần lượt là
Ta có
c) Ta có vectơ pháp tuyến của hai đường thẳng và lần lượt là
Ta có null
Suy ra
Vận dụng 5 trang 56 Toán lớp 10: Tìm số đo của góc giữa hai đường thẳng là đồ thị của hai hàm số và
Phương pháp giải:
Bước 1: Viết phương trình tổng quat từ đồ thị của hai hàm số đã cho
Bước 2: Xác định vectơ pháp tuyền
Bước 3:
Lời giải:
Từ đồ thị hàm số ta có phương trình tổng quát
,
Từ đó ta có vectơ pháp tuyến lần lượt là
Vậy góc giữa hai đường thẳng có đồ thị đã cho gần bằng
4. Khoảng cách từ một điểm đến một đường thẳng
a) Chứng minh rằng hai vectơ và cùng phương và tìm tọa độ của chúng
b) Gọi p là tích vô hướng của hai vectơ và .
Chứng minh rằng
c) Giải thích công thức
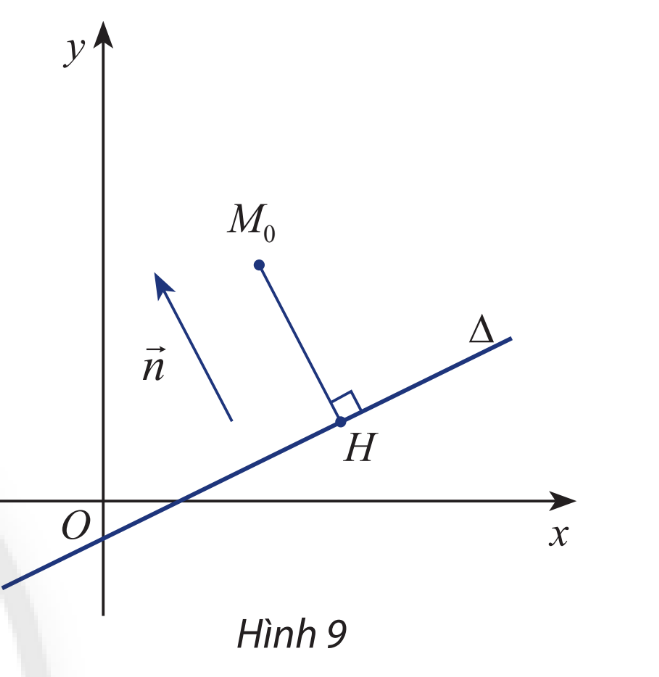
Phương pháp giải:
a) So sánh phương với vectơ chỉ phương
b) Bước 1: Nhân tích vô hướng của hai vectơ
Bước 2: Thay tọa độ điẻm H vào đường thẳng tìm mối liên hệ
c) Thay vào công thức kết quả đã tìm được ở câu b)
Lời giải:
a) Ta có: và
Mà H là hình chiếu vuông góc của trên nên
Mặt khác vectơ pháp tuyến cùng vuông góc với
Suy ra và cùng phương (đpcm)
b) Ta có: và
Suy ra (1)
Mà H thuộc đường thẳng nên tọa độ điểm H thỏa mãn phương trình đường thẳng
Thay tọa độ điểm H vào phương trình ta có:
Thay vào (1) ta có
(đpcm)
c) Ta có:
Giải toán lớp 10 trang 57 Tập 2 Chân trời sáng tạo
Phương pháp giải:
Bước 1: Viết phương trình tổng quat của các đường thẳng AB, AC, BC
Bước 2: Đường của kẻ từ A chính là khoảng cách từ điểm A đến đường thẳng BC (tương tự các đường cao còn lại)
Lời giải:
Ta có:
+) Đường thẳng AB nhận vectơ làm phương trình chỉ phương nên có vectơ pháp tuyến là và đi qua điểm , suy ra ta có phương trình tổng quát của đường thẳng AB là:
Độ dài đường cao kẻ từ C chính là khoảng cách từ điểm C đến đường thẳng AB
+) Đường thẳng BC nhận vectơ làm phương trình chỉ phương nên có vectơ pháp tuyến là và đi qua điểm , suy ra ta có phương trình tổng quát của đường thẳng BC là:
Độ dài đường cao kẻ từ A chính là khoảng cách từ điểm A đến đường thẳng BC
+) Đường thẳng AC nhận vectơ làm phương trình chỉ phương nên có vectơ pháp tuyến là và đi qua điểm , suy ra ta có phương trình tổng quát của đường thẳng AC là:
Độ dài đường cao kẻ từ B chính là khoảng cách từ điểm B đến đường thẳng AC
Vận dụng 6 trang 57 Toán lớp 10: Tính khoảng cách giữa hai đường thẳng và
Phương pháp giải:
Khoảng cách giữa hai đường thẳng song song là khoảng cách một điềm bất kì từ đường thẳng này tới đường thẳng còn lại
Lời giải:
Ta thấy hai đường thẳng này song song, nên khoảng cách giữa chúng là khoảng cách từ một điểm bất kì từ đường thẳng này tới đường thẳng kia
Chọn điểm , suy ra
Vậy khoảng cách giữa hai đường thẳng và là 2
Bài tập (trang 57, 58)
a) d đi qua điểm và có vectơ chỉ phương
b) d đi qua điểm và có vectơ pháp tuyến là
c) d đi qua và có hệ số góc
d) d đi qua hai điểm và
Lời giải:
a) Đường thẳng đi qua điểm và có vectơ chỉ phương , nên có phương trình tham số là:
Đường thẳng có vectơ chỉ phương ,nên có vectơ pháp tuyền là và đi qua
Ta có phương trình tổng quát là
b) Đường thẳng có vectơ pháp tuyến nên có vectơ chỉ phương , và đi qua điểm nên ta có phương trình tham số của là :
Đường thẳng đi qua điểm và có vectơ pháp tuyến
Phương trình tổng quát của đường thẳng d là:
c) Đường thẳng có dạng
d đi qua và có hệ số góc nên ta có:
Suy ra đồ thị đường thẳng d có dạng
Vậy đường thẳng d có phương trình tổng quát là
Suy ra đường thẳng d có vectơ pháp tuyến , nên có vectơ chỉ phương là và đi qua điểm nên ta có phương trình tham số của d là :
d) Đường thẳng đi qua hai điểm và nên có vectơ chỉ phương và có vectơ pháp tuyến
Phương trình tham số của là:
Phương trình tổng quát của là:
Bài 2 trang 57 Toán lớp 10: Cho tam giác ABC biết và
a) Lập phương trình tổng quát của đường thẳng BC
b) Lập phương trình tham số của đường trung tuyến AM
c) Lập phương trình của đường cao AH
Lời giải:
a) Ta có:
Phương trình tổng quát của đường thẳng BC đi qua điểm và nhận vectơ làm VTPT là:
b) M là trung điểm của BC nên ta có tọa độ điểm M là
Đường thẳng AM đi qua điểm và nhận vectơ làm vectơ chỉ phương nên ta có phương trình tham số của trung tuyến AM là:
c) Ta có: nên đường cao AH nhận vectơ làm vectơ pháp tuyến
Đường thẳng AH đi qua và nhận vectơ làm vectơ pháp tuyến, suy ta phương trình tổng quát của đường cao AH là:
a) đi qua và song song với đường thẳng
b) đi qua và vuông góc với đường thẳng
Phương pháp giải:
Bước 1: Từ đường thẳng đã cho xác định vectơ pháp tuyến hoặc vectơ chỉ phương
Bước 2: Viết phương trình tổng quát và phương trình tham số
Lời giải:
a) song song với đường thẳng nên nhận vectơ pháp tuyến của đường thẳng này làm vectơ pháp tuyến là
đi qua điểm nên ta có phương trình tổng quát
có vectơ pháp tuyến nên có vectơ chỉ phương là
Phương trình tham số của đường thẳng là:
b) vuông góc với đường thẳng nên nhận vectơ pháp tuyến của đường thẳng này làm vectơ chỉ phương là
đi qua điểm nên ta có phương trình tham số:
có vectơ chỉ phương nên có vectơ pháp tuyến là
Phương trình tổng quát của đường thẳng là:
Bài 4 trang 57 Toán lớp 10: Xét vị trí tương đối của cặp đường thẳng và sau đây:
a) và
b) và
c) và
Phương pháp giải:
Bước 1: Xác định cặp vectơ pháp tuyến (hoặc chỉ phương) của hai đường thẳng:
Bước 2:
+) Nếu 2 vecto cùng phương: Lấy điểm A thuộc d1. Kiểm tra A có thuộc d2 hay không.
=> KL: 2 đường thẳng song song nếu A không thuộc d2.
2 đường thẳng trùng nhau nếu A thuộc d2.
+) Nếu 2 vecto không cùng phương: Tính tích vô hướng
Nếu bằng 0 thì hai đường thẳng vuông góc, nếu khác 0 thì 2 đường thẳng chỉ cắt nhau.
=> Giải hệ phương trình từ hai đường thẳng để tìm giao điểm
Lời giải:
a) và có vectơ pháp tuyến lần lượt là
Ta có nên
Giải hệ phương trình ta được nghiệm
Suy ra hai đường thẳng và vuông góc và cắt nhau tại
b) và có vectơ pháp tuyến lần lượt là
trùng nhau nên hai vectơ pháp tuyến cùng phương. Suy ra và song song hoặc trùng nhau
Lấy điểm thuộc , thay tọa độ của A vào phương trình , ta được , suy ra A không thuộc đường thẳng
Vậy hai đường thẳng và song song
c) và có vectơ pháp tuyến lần lượt là
Suy ra hai vectơ pháp tuyến cùng phương. Suy ra và song song hoặc trùng nhau
Lấy điểm thuộc , thay tọa độ của A vào phương trình , ta được , suy ra A thuộc đường thẳng
Vậy hai đường thẳng và trùng nhau
Giải toán lớp 10 trang 58 Tập 2 Chân trời sáng tạo
Bài 5 trang 58 Toán lớp 10: Cho đường thẳng d có phương trình tham số
Tìm giao điểm của d với hai trục tọa độ
Phương pháp giải:
+) A là giao của d với Ox => A(a;0) thuộc d.
+) A là giao của d với Oy => A(0;a') thuộc d.
Lời giải:
+) Gọi A là giao điểm của đường thẳng d với trục tung
Suy ra tọa độ của A là:
Thay vào phương trình ta có:
Vậy giao điểm của d với trục tung là
+) Gọi B là giao điểm của đường thẳng d với trục hoành
Suy ra tọa độ của B là:
Thay vào phương trình ta có:
Vậy giao điểm của d với trục hoành là
Bài 6 trang 58 Toán lớp 10: Tìm số đo của góc giữa hai đường thẳng và trong các trường hợp sau:
a) và
b) và
c) và
Phương pháp giải:
Bước 1: Xác định 2 vectơ pháp tuyến (hoặc chỉ phương) của hai đường thẳng đã cho:
Bước 2: Tính cos góc giữa hai đường thẳng bằng công thức => suy ra góc giữa 2 đt.
Lời giải:
a) Ta có vectơ pháp tuyến của hai đường thẳng và lần lượt là
Ta có
b) Ta có vectơ pháp tuyến của hai đường thẳng và lần lượt là
Ta có
Suy ra
c) Ta có vectơ chỉ phương của hai đường thẳng và lần lượt là
Bài 7 trang 58 Toán lớp 10: Tính khoảng cách từ điểm M đến đường thẳng trong các trường hợp sau:
a) và
b) và
c) và
d) và
Phương pháp giải:
Bước 1: Xác định phương trình tổng quát của
Bước 2: khoảng cách từ đến d là:
Lời giải:
a) Khoảng cách từ đến là:
b) có phương trình tham số nên có phương trình tổng quát là
Suy ra khoảng cách từ điểm đến đường thẳng là
c) có phương trình tham số nên có phương trình tổng quát là
Suy ra khoảng cách từ điểm đến đường thẳng là
d) Khoảng cách từ đến là:
Bài 8 trang 58 Toán lớp 10: Tính khoảng cách giữa hai đường thẳng và
Phương pháp giải:
+) Khoảng cách giữa hai đường thẳng song song là khoảng cách một điểm bất kì từ đường thẳng này tới đường thẳng còn lại
+) khoảng cách từ đến d là:
Lời giải:
Ta có vectơ pháp tuyến của hai đường thẳng là suy ra hai đường thẳng này song song, nên khoảng cách giữa chúng là khoảng cách từ một điểm bất kì từ đường thẳng này tới đường thẳng kia
Chọn điểm , suy ra
Vậy khoảng cách giữa hai đường thẳng và là
Phương pháp giải:
Khi M nằm trên đường thẳng d thì khoảng ngắn nhất là đoạn vuông góc
Lời giải:
Điểm S nằm trên đường thẳng d , nên khi S di động trên đoạn thẳng d thì SM ngắn nhất khi
Nên khoảng cách ngắn nhất từ điểm đến điểm S là khoảng cách từ điểm đến d
Khoảng cách đó là:
Vậy khi S di động trên đường thẳng d thì khoảng cách ngắn nhất từ điểm đến điểm S là 2.
a) Viết phương trình các đường thẳng AB, AC, BC
b) Tính góc hợp bởi hai đường thẳng AB và AC
c) Tính khoảng cách từ điểm A đến đường thẳng BC
Phương pháp giải:
a) Tìm VTPT (hoặc VTCP) => Lập PT tổng quát (hoặc tham số) của đt.
b) Xác định góc giữa hai đường thẳng thông qua cặp VTPT ( hoặc VTCP):
c) Khoảng cách từ đến BC: là
Lời giải:
a) Ta có:
+) Đường thẳng AB nhận vectơ làm phương trình chỉ phương và đi qua điểm nên có phương trình tham số là:
+) Đường thẳng AC nhận vectơ làm phương trình chỉ phương và đi qua điểm nên có phương trình tham số là:
+) Đường thẳng BC nhận vectơ làm phương trình chỉ phương và đi qua điểm nên có phương trình tham số là:
b) Ta có vectơ pháp tuyến của hai đường thẳng AB và AC lần lượt là:
Vậy góc giữa hai đường thẳng AB và AC là
c) Đường thẳng BC nhận vectơ làm vectơ chỉ phương nên có vectơ pháp tuyến là và đi qua , suy ra phương trình tổng quát của đường thẳng BC là:
Khoảng cách từ đến đường thẳng BC là:
Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Đường tròn trong mặt phẳng tọa độ
Bài 4: Ba đường conic trong mặt phẳng tọa độ
Lý thuyết Đường thẳng trong mặt phẳng tọa độ
1. Phương trình đường thẳng
1.1. Vectơ chỉ phương và vectơ pháp tuyến của đường thẳng
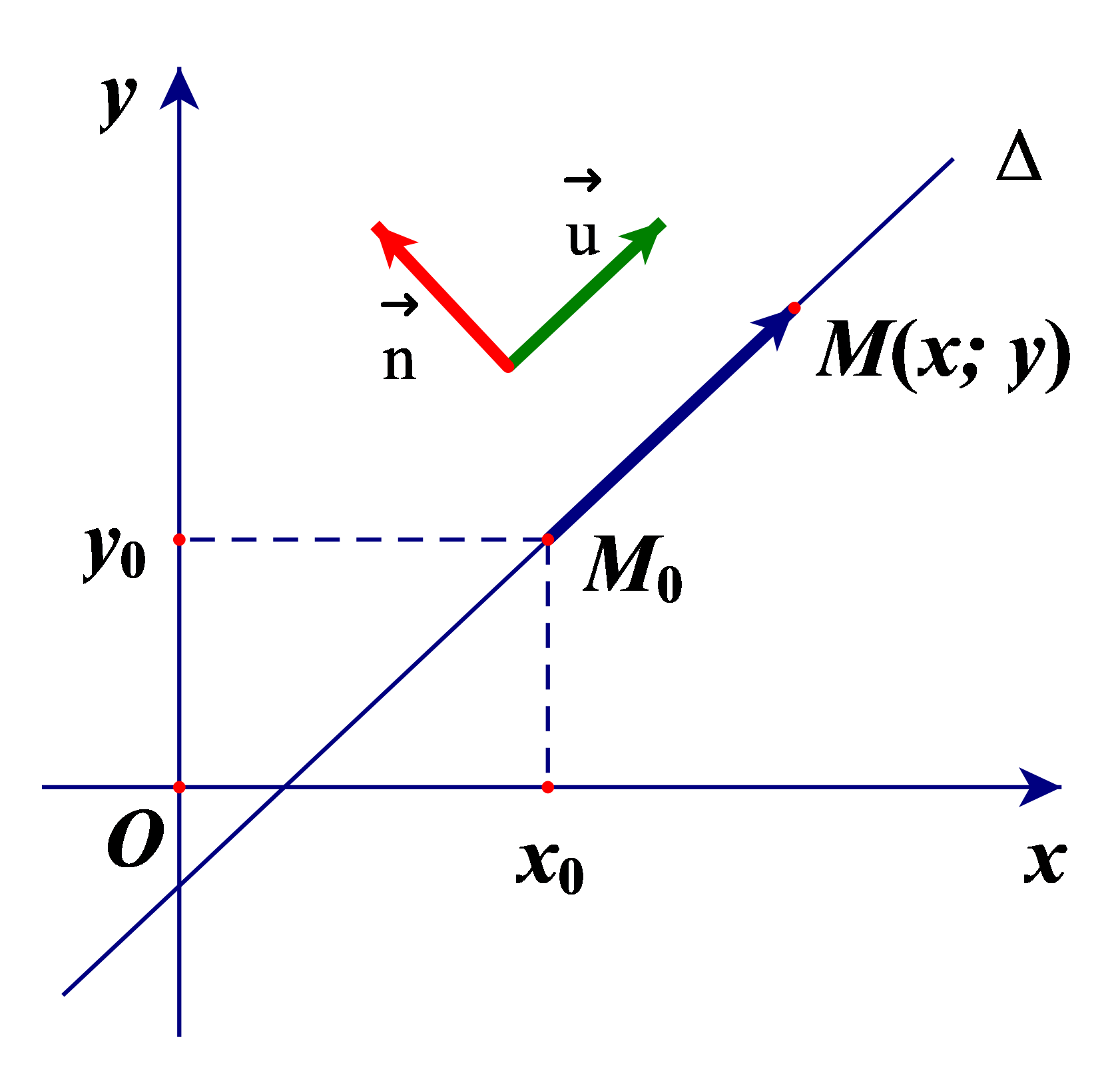 Vectơ được gọi là vectơ chỉ phương của đường thẳng ∆ nếu và giá của song song hoặc trùng với ∆.
Vectơ được gọi là vectơ chỉ phương của đường thẳng ∆ nếu và giá của song song hoặc trùng với ∆.
Vectơ được gọi là vectơ pháp tuyến của đường thẳng ∆ nếu và vuông góc với vectơ chỉ phương của ∆.
Chú ý:
• Nếu đường thẳng ∆ có vectơ pháp tuyến thì ∆ sẽ nhận hoặc là một vectơ chỉ phương.
• Nếu là vectơ chỉ phương của đường thẳng ∆ thì (k ≠ 0) cũng là vectơ chỉ phương của ∆.
• Nếu là vectơ pháp tuyến của đường thẳng ∆ thì (k ≠ 0) cũng là vectơ pháp tuyến của ∆.
Ví dụ:
a) Cho đường thẳng d có vectơ chỉ phương . Tìm một vectơ pháp tuyến của d.
b) Cho đường thẳng d’ có vectơ pháp tuyến . Tìm ba vectơ chỉ phương của d’.
Hướng dẫn giải
a) Đường thẳng d có vectơ chỉ phương .
Suy ra d cũng có vectơ chỉ phương và có vectơ pháp tuyến .
Vậy d có vectơ pháp tuyến .
b)
• d’ có vectơ pháp tuyến .
Suy ra d’ có vectơ chỉ phương ; .
• d’ có vectơ chỉ phương .
Suy ra d’ cũng có vectơ chỉ phương .
Vậy ba vectơ chỉ phương của d’ là ; ; .
1.2. Phương trình tham số của đường thẳng
Trong mặt phẳng Oxy, ta gọi:
(với )
là phương trình tham số của đường thẳng ∆ đi qua điểm M0(x0; y0), có vectơ chỉ phương .
Chú ý: Cho t một giá trị cụ thể thì ta xác định được một điểm trên đường thẳng ∆ và ngược lại.
Ví dụ:
a) Viết phương trình tham số của đường thẳng d đi qua điểm M(1; 3) và nhận làm vectơ chỉ phương.
b) Trong các điểm A(2; 5), B(3; 12), C(–4; 6) thì điểm nào thuộc đường thẳng d?
Hướng dẫn giải
a) Đường thẳng d đi qua điểm M(1; 3) và có vectơ chỉ phương .
Vậy phương trình tham số của đường thẳng d:
b)
• Thay tọa độ điểm A vào phương trình tham số của đường thẳng d, ta được:
(vô lý).
Khi đó A(2; 5) ∉ d.
• Thay tọa độ điểm B vào phương trình tham số của đường thẳng d, ta được:
.
Khi đó B(3; 12) ∈ d.
• Thay tọa độ điểm C vào phương trình tham số của đường thẳng d, ta được:
(vô lý).
Khi đó C(–4; 6) ∉ d.
Vậy chỉ có điểm B thuộc đường thẳng d.
1.3. Phương trình tổng quát của đường thẳng
Trong mặt phẳng Oxy, mỗi đường thẳng đều có phương trình tổng quát dạng: ax + by + c = 0, với a và b không đồng thời bằng 0.
Chú ý:
• Mỗi phương trình ax + by + c = 0 (a và b không đồng thời bằng 0) đều xác định một đường thẳng có vectơ pháp tuyến .
• Khi cho phương trình đường thẳng ax + by + c = 0, ta hiểu a và b không đồng thời bằng 0.
Ví dụ: Viết phương trình tổng quát của đường thẳng ∆ trong mỗi trường hợp sau:
a) Đường thẳng ∆ đi qua điểm H(2; 1) và có vectơ pháp tuyến .
b) Đường thẳng ∆ đi qua điểm K(5; –8) và có vectơ chỉ phương .
c) Đường thẳng ∆ đi qua hai điểm M(6; 3), N(9; 1).
Hướng dẫn giải
a) Đường thẳng ∆ đi qua điểm H(2; 1) và có vectơ pháp tuyến nên ta có phương trình tổng quát của ∆ là: –2(x – 2) – 1(y – 1) = 0
⇔ –2x – y + 5 = 0.
Vậy phương trình tổng quát của ∆ là –2x – y + 5 = 0.
b) ∆ có vectơ chỉ phương nên ∆ nhận làm vectơ pháp tuyến.
Đường thẳng ∆ đi qua điểm K(5; –8) và có vectơ pháp tuyến nên ta có phương trình tổng quát của ∆ là: 4(x – 5) + 3(y + 8) = 0
⇔ 4x + 3y + 4 = 0.
Vậy phương trình tổng quát của ∆ là 4x + 3y + 4 = 0.
c) Với M(6; 3), N(9; 1) ta có: .
∆ có vectơ chỉ phương nên ∆ nhận làm vectơ pháp tuyến.
Đường thẳng ∆ đi qua điểm M(6; 3) và có vectơ pháp tuyến nên phương trình tổng quát của ∆ là: 2(x – 6) + 3(y – 3) = 0
⇔ 2x + 3y – 21 = 0.
Vậy phương trình tổng quát của ∆ là 2x + 3y – 21 = 0.
Nhận xét:
• Phương trình đường thẳng ∆ đi qua hai điểm A(xA; yA), B(xB; yB) có dạng:
(với xB ≠ xA, yB ≠ yA).
• Nếu đường thẳng ∆ cắt trục Ox và Oy tại A(a; 0) và B(0; b) (a, b khác 0) thì phương trình ∆ có dạng:
(1).
Phương trình (1) còn được gọi là phương trình đoạn chắn.
Ví dụ:
+) Đường thẳng ∆ đi qua hai điểm P(2; 5), Q(1; 8).
Suy ra phương trình đường thẳng ∆: .
Vậy phương trình đường thẳng ∆ là .
+) Đường thẳng ∆ đi qua hai điểm X(–4; 0) và Y(0; 5).
Vậy phương trình đoạn chắn của ∆: .
1.4. Liên hệ giữa đồ thị hàm số bậc nhất và đường thẳng
Ta đã biết đồ thị của hàm số bậc nhất y = kx + y0 (k ≠ 0) là một đường thẳng d đi qua điểm M(0; y0) và có hệ số góc k. Ta có thể viết: y = kx + y0 ⇔ kx – y + y0 = 0.
Như vậy, đồ thị hàm bậc nhất y = kx + y0 là một đường thẳng có vectơ pháp tuyến và có phương trình tổng quát là kx – y + y0 = 0. Đường thẳng này không vuông góc với Ox và Oy.
Ngược lại, cho đường thẳng d có phương trình tổng quát ax + by + c = 0 với a và b đều khác 0, khi đó ta có thể viết: ax + by + c = 0 ⇔ y = kx + y0.
Như vậy d là đồ thị của hàm bậc nhất y = kx + y0 với hệ số góc và tung độ gốc .
Ví dụ:
+) Cho đường thẳng d có phương trình: y = 2x + 1 ⇔ 2x – y + 1 = 0.
Ta suy ra vectơ pháp tuyến của đường thẳng d là .
+) Cho đường thẳng d’ có phương trình: x + 5y – 2 = 0 .
Khi đó ta có d là đồ thị của hàm bậc nhất y = kx + y0, với hệ số góc và tung độ gốc .
Chú ý:
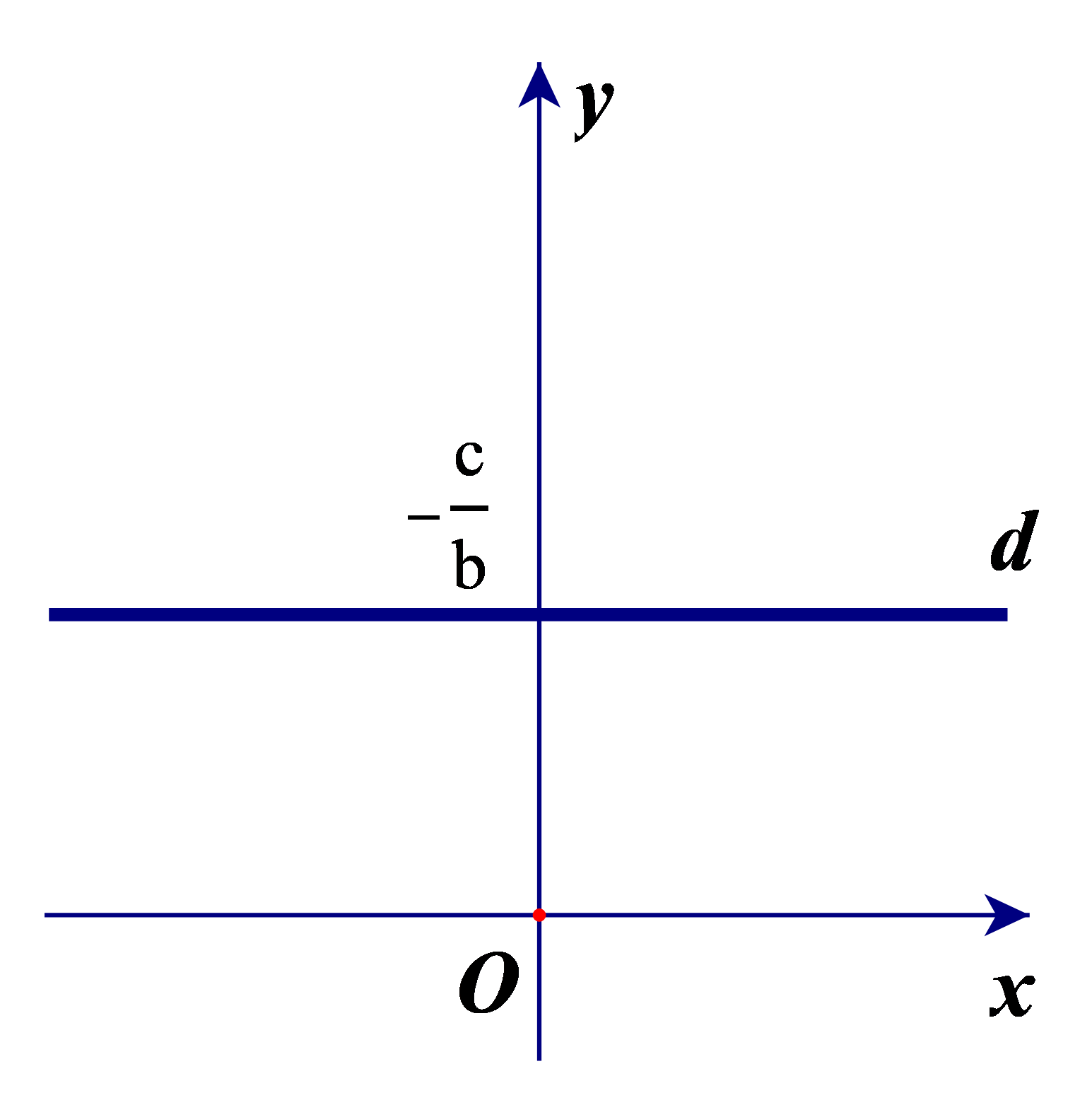
• Nếu a = 0 và b ≠ 0 thì phương trình tổng quát ax + by + c = 0 trở thành .
Khi đó d là đường thẳng vuông góc với Oy tại điểm .
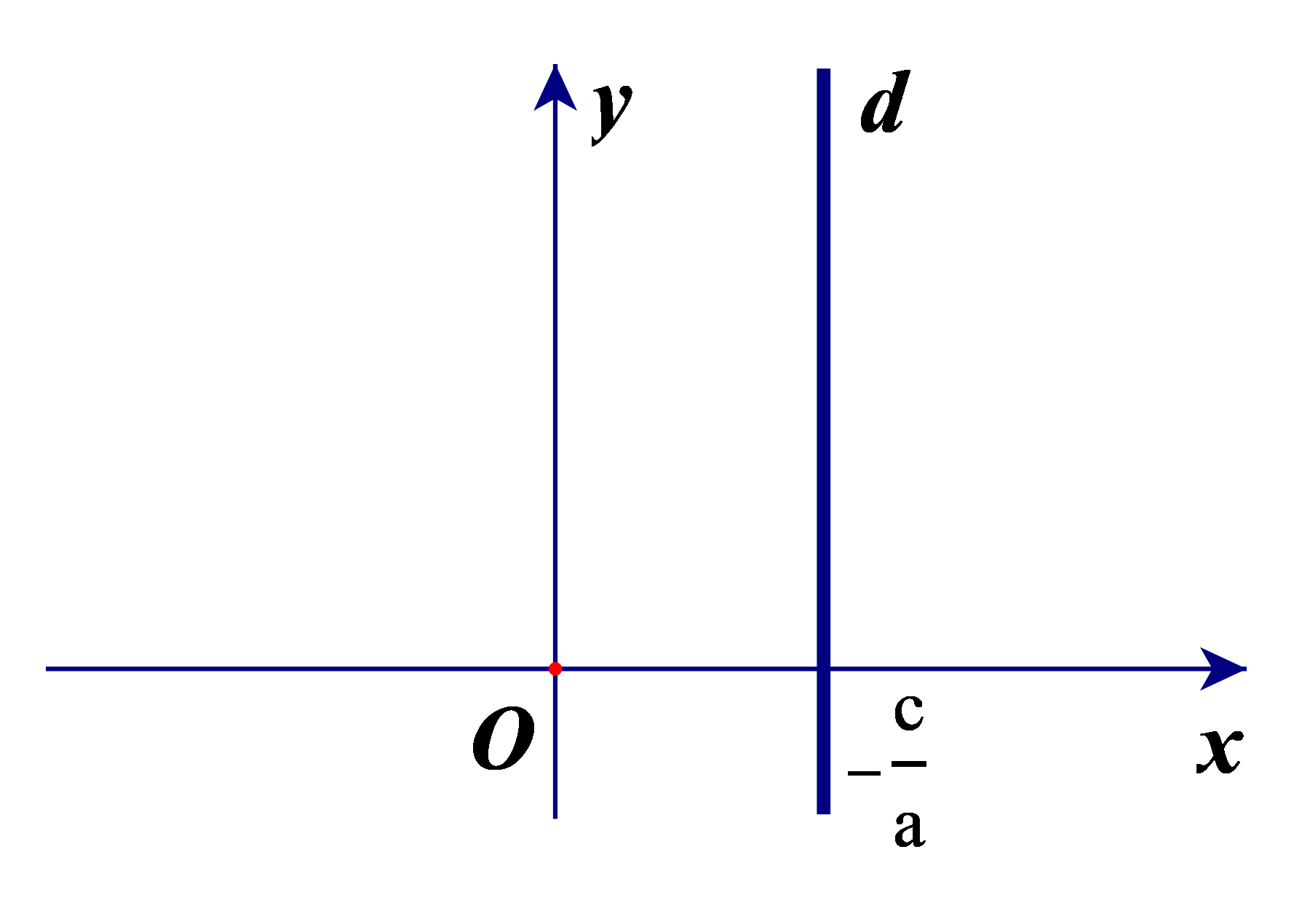
• Nếu b = 0 và a ≠ 0 thì phương trình tổng quát ax + by + c = 0 trở thành .
Khi đó d là đường thẳng vuông góc với Ox tại điểm .
 Trong cả hai trường hợp trên, đường thẳng d không phải là đồ thị của hàm số bậc nhất.
Trong cả hai trường hợp trên, đường thẳng d không phải là đồ thị của hàm số bậc nhất.
2. Vị trí tương đối của hai đường thẳng
Trong mặt phẳng Oxy, cho hai đường thẳng ∆1: a1x + b1y + c1 = 0 () có vectơ pháp tuyến và đường thẳng ∆2: a2x + b2y + c2 = 0 () có vectơ pháp tuyến .
Ta có thể dùng phương pháp tọa độ để xét vị trí tương đối của ∆1 và ∆2 như sau:
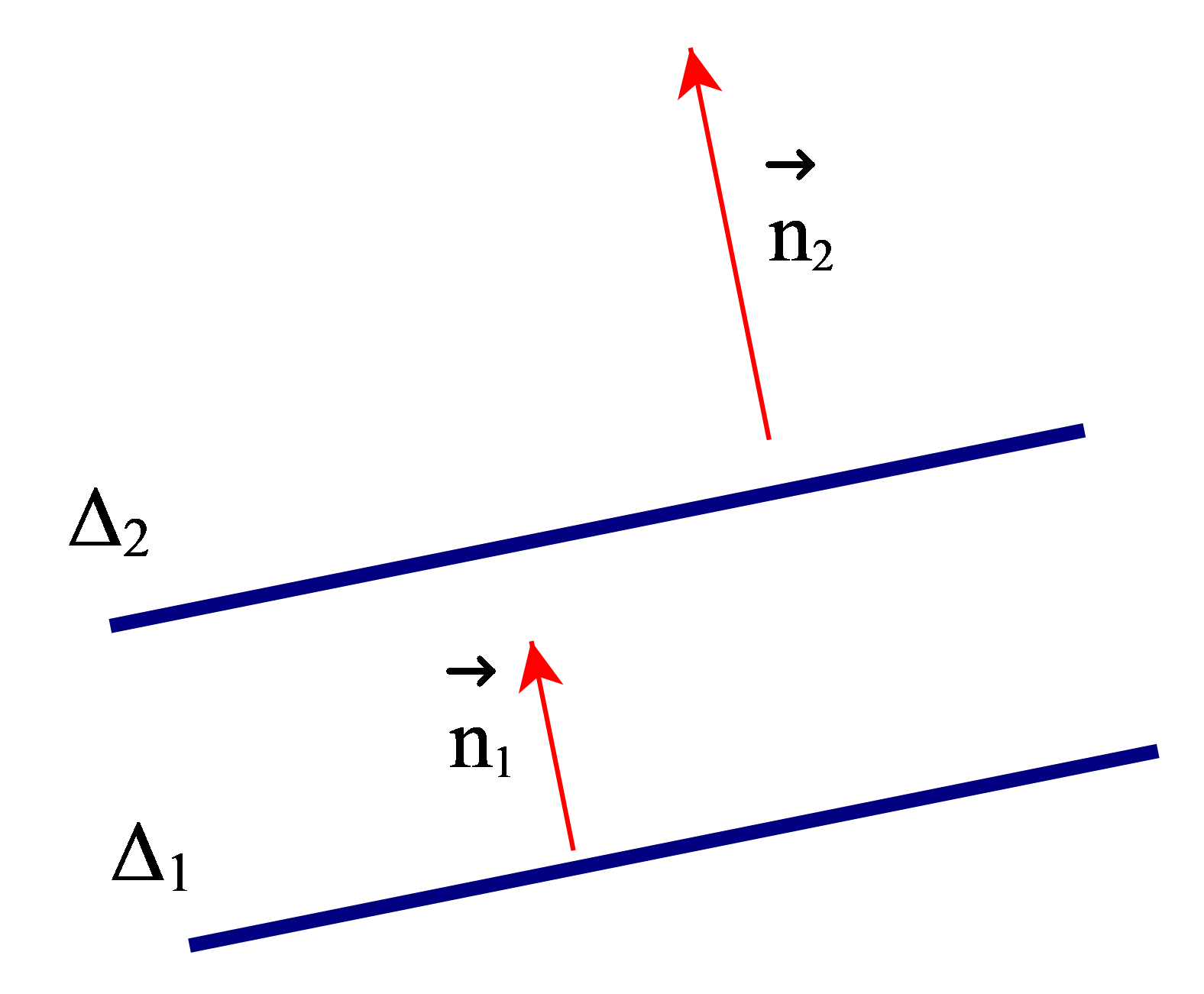
– Nếu và cùng phương thì ∆1 và ∆2 song song hoặc trùng nhau. Lấy một điểm P tùy ý trên ∆1.
+ Nếu P ∈ ∆2 thì ∆1 ≡ ∆2.
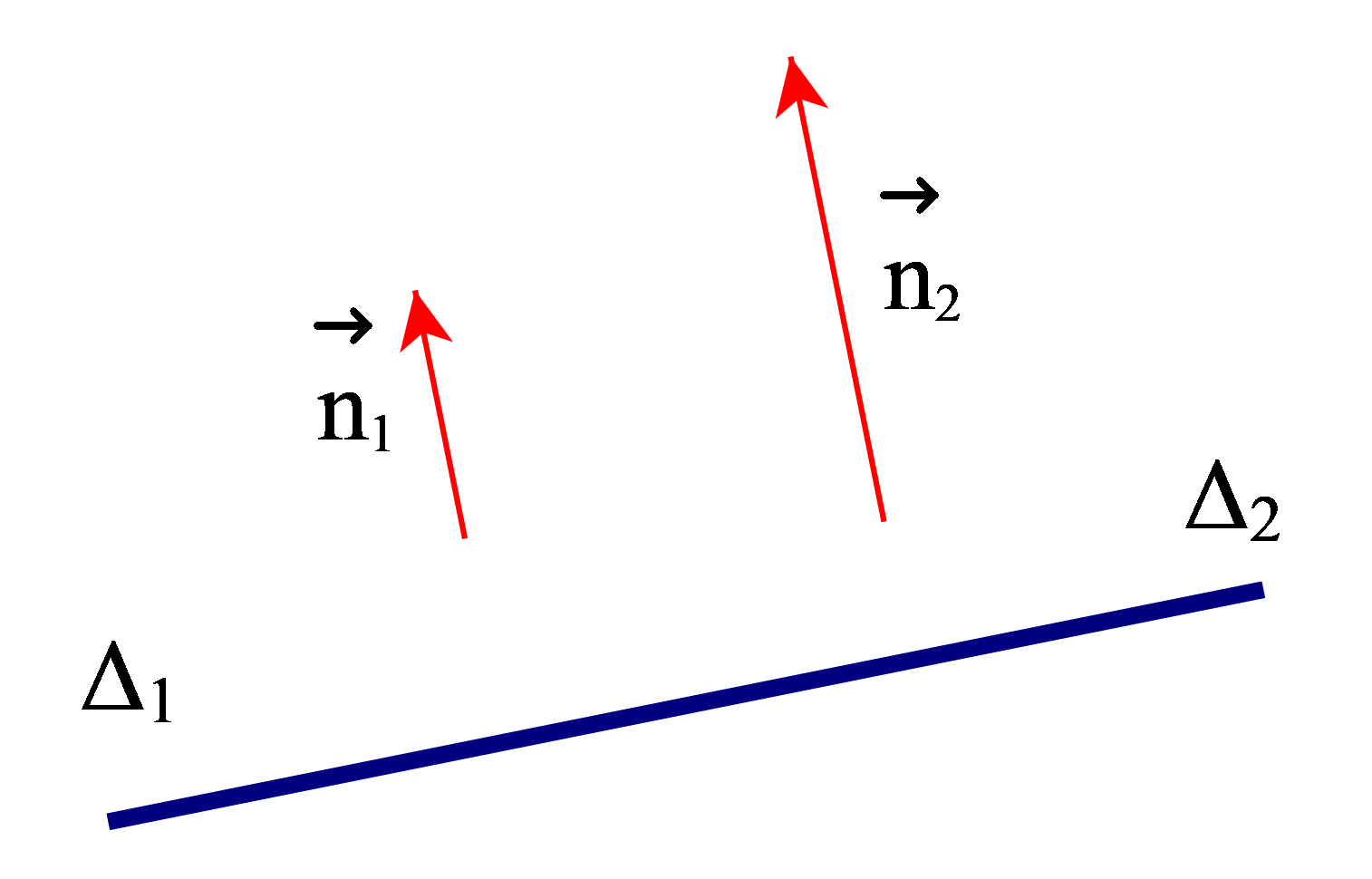
+ Nếu P ∉ ∆2 thì ∆1 // ∆2.
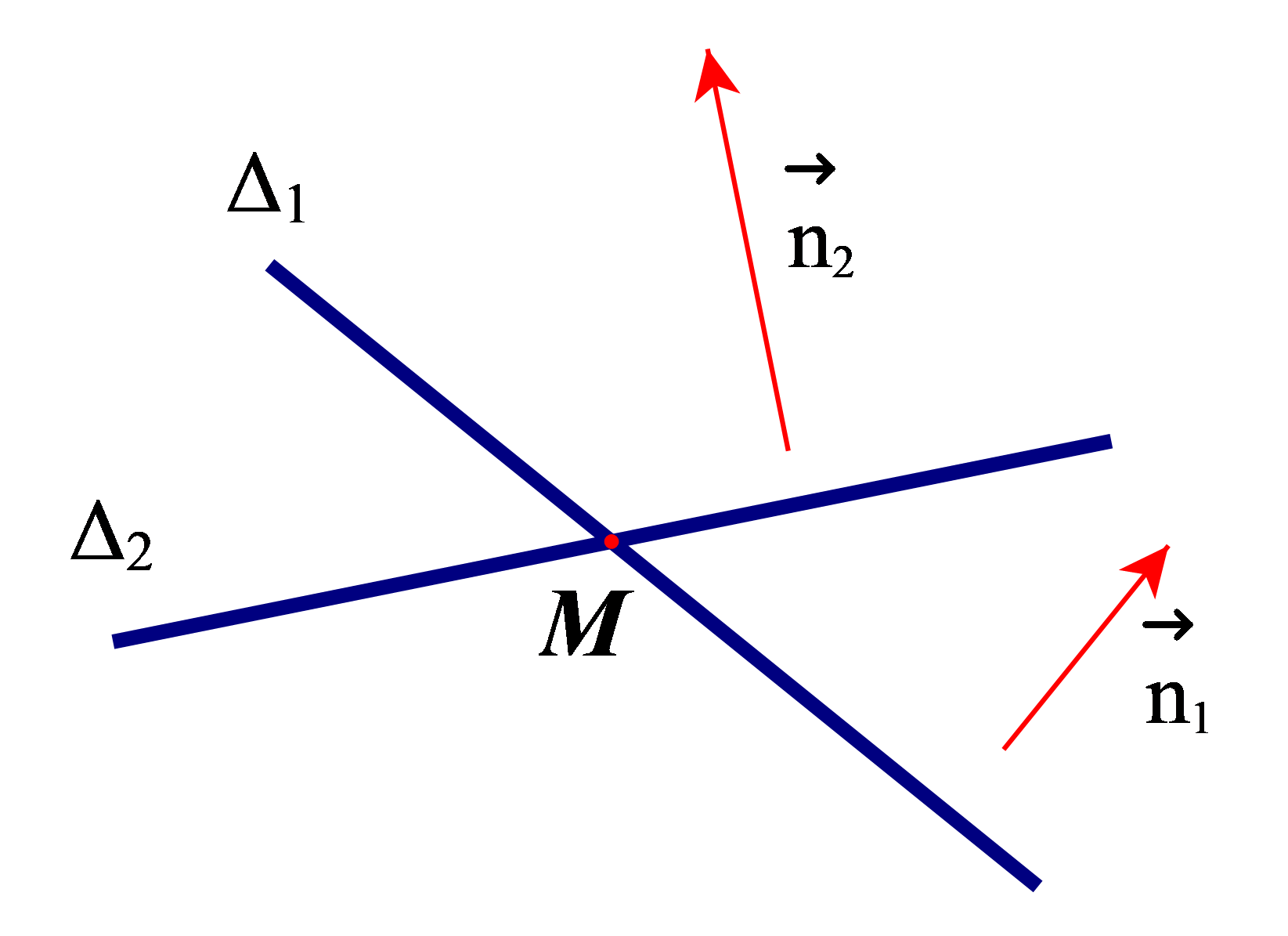
– Nếu và không cùng phương thì ∆1 và ∆2 cắt nhau tại một điểm M(x0; y0) với (x0; y0) là nghiệm của hệ phương trình: .
Chú ý:
a) Nếu thì , suy ra ∆1 ⊥ ∆2.
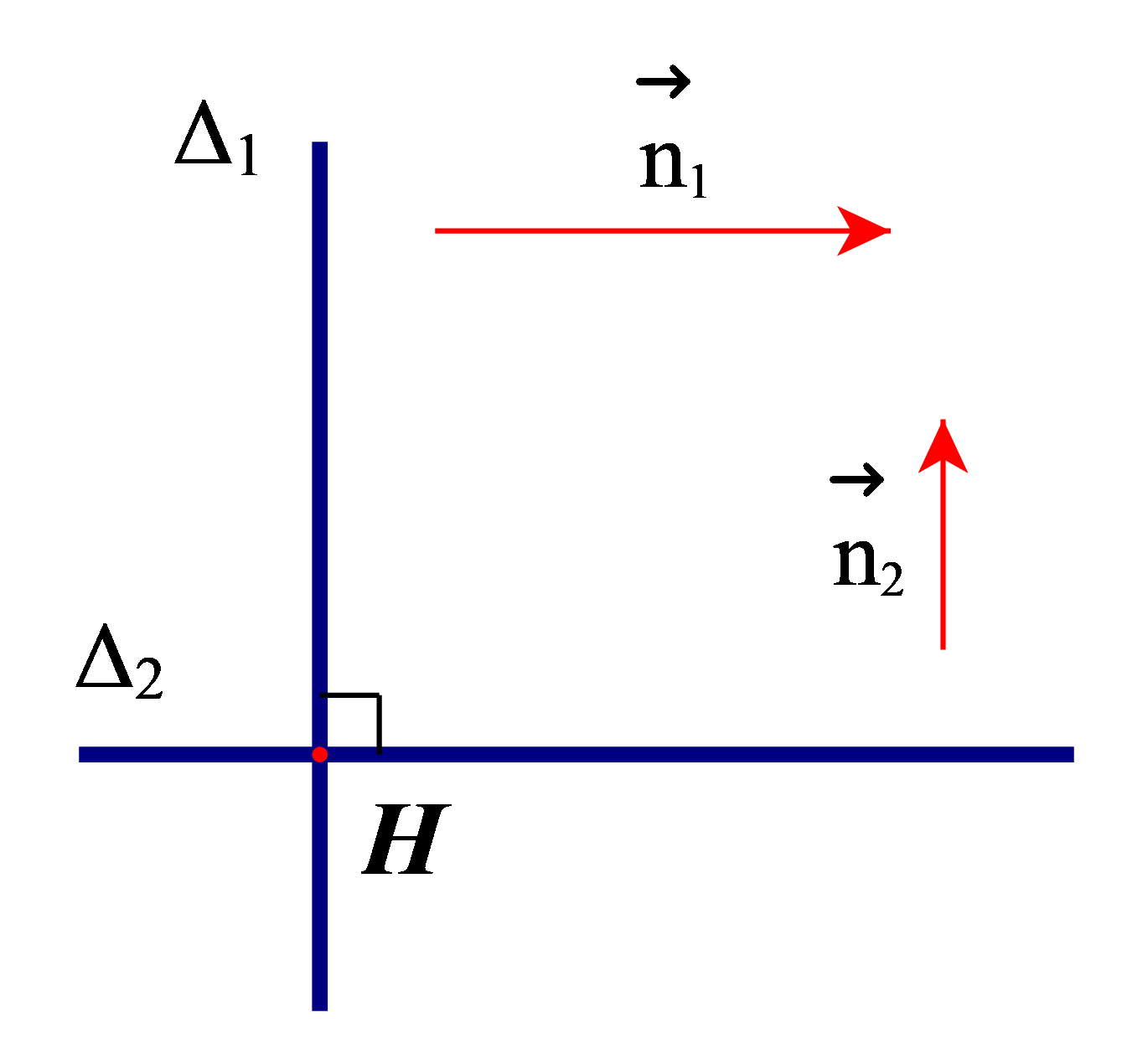
b) Để xét hai vectơ và cùng phương hay không cùng phương, ta xét biểu thức a1b2 – a2b1:
+ Nếu a1b2 – a2b1 = 0 thì hai vectơ cùng phương.
+ Nếu a1b2 – a2b1 ≠ 0 thì hai vectơ không cùng phương.
Trong trường hợp tất cả các hệ số a1, a2, b1, b2 đều khác 0, ta có thể xét hai trường hợp:
+ Nếu thì hai vectơ cùng phương.
+ Nếu thì hai vectơ không cùng phương.
Ví dụ: Xét vị trí tương đối của các cặp đường thẳng sau:
a) ∆1: 4x – 10y + 1 = 0 và ∆2: x + y + 2 = 0.
b) ∆1: 12x – 6y + 6 = 0 và ∆2: 2x – y + 5 = 0.
c) ∆1: 8x + 10y – 12 = 0 và ∆2:
d) ∆1: và ∆2:
Hướng dẫn giải
a) ∆1: 4x – 10y + 1 = 0 và ∆2: x + y + 2 = 0.
∆1 và ∆2 có vectơ pháp tuyến lần lượt là và .
Ta có .
Suy ra và là hai vectơ không cùng phương.
Khi đó ta có ∆1 và ∆2 cắt nhau tại một điểm M.
Giải hệ phương trình:
Suy ra .
Vậy ∆1 cắt ∆2 tại điểm .
b) ∆1: 12x – 6y + 6 = 0 và ∆2: 2x – y + 5 = 0.
∆1 và ∆2 có vectơ pháp tuyến lần lượt là và .
Ta có .
Suy ra và là hai vectơ cùng phương.
Khi đó ta có ∆1 và ∆2 song song hoặc trùng nhau.
Chọn M(0; 1) ∈ ∆1.
Thay tọa độ điểm M vào phương trình đường thẳng ∆2, ta được: 2.0 – 1 + 5 = 4 ≠ 0.
Suy ra M(0; 1) ∉ ∆2.
Vậy ∆1 // ∆2.
c) ∆1: 8x + 10y – 12 = 0 và ∆2:
∆1 có vectơ pháp tuyến .
∆2 có vectơ chỉ phương .
Suy ra ∆2 có vectơ pháp tuyến .
Ta có .
Suy ra và là hai vectơ cùng phương.
Khi đó ta có ∆1 và ∆2 song song hoặc trùng nhau.
Chọn M(–6; 6) ∈ ∆2.
Thế tọa độ điểm M vào phương trình đường thẳng ∆1, ta được: 8.(–6) + 10.6 – 12 = 0.
Suy ra M(–6; 6) ∈ ∆1.
Vậy ∆1 ≡ ∆2.
d) ∆1: và ∆2:
• ∆1 có vectơ chỉ phương .
Suy ra ∆1 có vectơ pháp tuyến .
• ∆2 có vectơ chỉ phương .
Suy ra ∆2 có vectơ pháp tuyến .
∆1 và ∆2 có vectơ pháp tuyến lần lượt là và .
Ta có 4.5 + 5.(–4) = 0.
Suy ra .
Do đó ∆1 ⊥ ∆2.
∆1 đi qua điểm A(–1; 2) và có vectơ pháp tuyến .
Suy ra phương trình tổng quát của ∆1: 4(x + 1) + 5(y – 2) = 0 ⇔ 4x + 5y – 6 = 0.
Tương tự, ta tìm được phương trình tổng quát của ∆2: 5x – 4y + 38 = 0.
Gọi M(x; y) là giao điểm của ∆1 và ∆2.
Suy ra tọa độ điểm M thỏa hệ phương trình:
Khi đó ta có tọa độ là .
Vậy ∆1 và ∆2 vuông góc với nhau tại điểm .
3. Góc giữa hai đường thẳng
3.1. Khái niệm góc giữa hai đường thẳng
Hai đường thẳng ∆1 và ∆2 cắt nhau tạo thành bốn góc.
• Nếu ∆1 không vuông góc với ∆2 thì góc nhọn trong bốn góc đó được gọi là góc giữa hai đường thẳng ∆1 và ∆2.
• Nếu ∆1 vuông góc với ∆2 thì ta nói góc giữa ∆1 và ∆2 bằng 90°.
Ta quy ước: Nếu ∆1 và ∆2 song song hoặc trùng nhau thì góc giữa ∆1 và ∆2 bằng 0°.
Như vậy góc α giữa hai đường thẳng luôn thỏa mãn: 0° ≤ α ≤ 90°.
Góc giữa hai đường thẳng ∆1 và ∆2 được kí hiệu là hoặc (∆1, ∆2).
Ví dụ: Cho hình chữ nhật ABCD có .
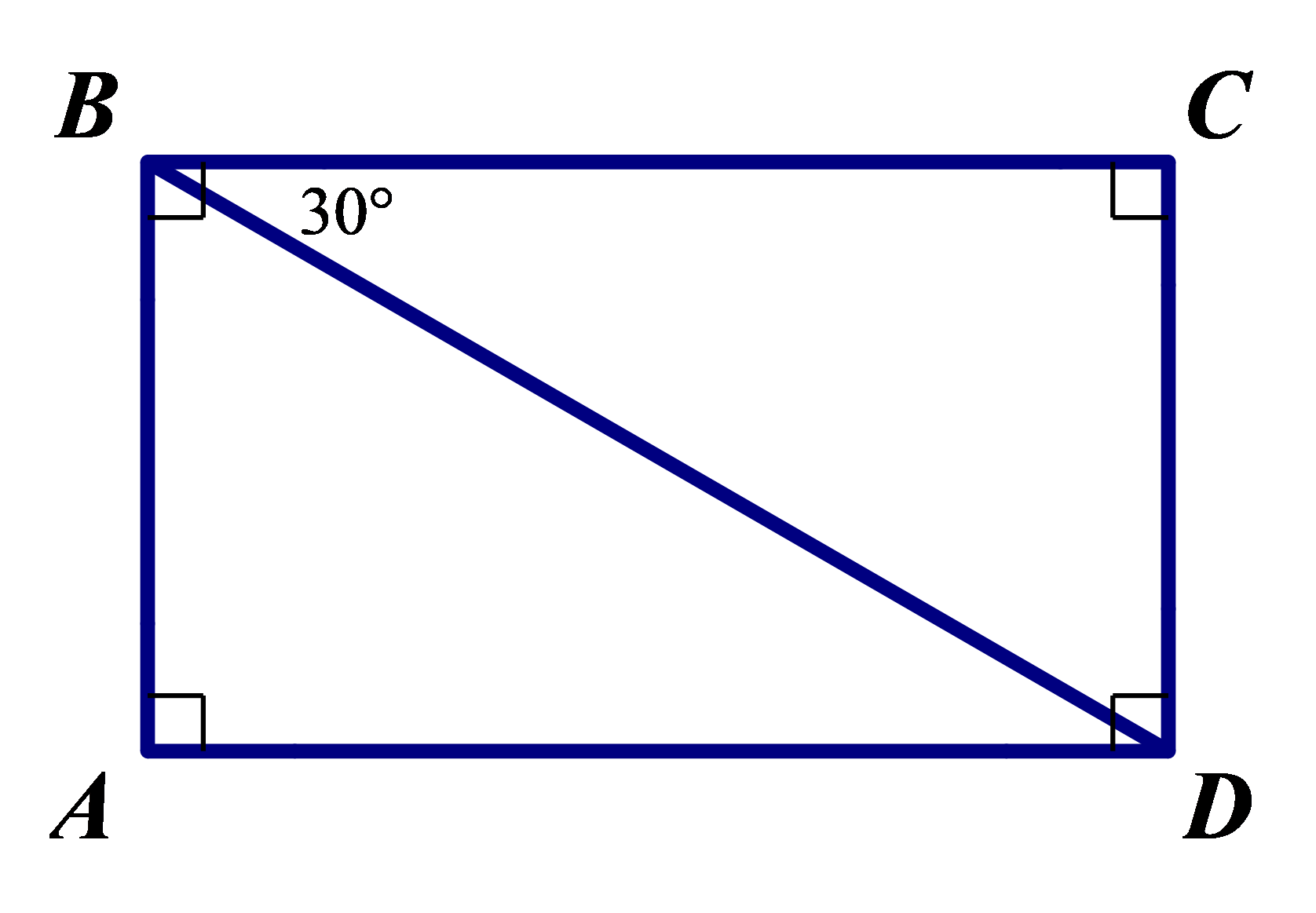 Tính các góc: (BD, BC), (AB, AD), (AD, BC), (AB, BD).
Tính các góc: (BD, BC), (AB, AD), (AD, BC), (AB, BD).
Hướng dẫn giải
Ta có:
+) . Suy ra (BD, BC) = 30°.
+) Vì AB ⊥ AD nên (AB, AD) = 90°.
+) Vì AD // BC nên (AD, BC) = 0°.
+) Ta có (Vì AB ⊥ BC).
.
Vì nên (AB, BD) = 60°.
Vậy (BD, BC) = 30°, (AB, AD) = 90°, (AD, BC) = 0°, (AB, BD) = 60°.
3.2. Công thức tính góc giữa hai đường thẳng
Đường thẳng ∆1 và ∆2 có vectơ pháp tuyến lần lượt là .
Ta có công thức: .
Nhận xét: Nếu ∆1, ∆2 có vectơ chỉ phương thì .
Chú ý: Ta đã biết hai đường thẳng vuông góc khi và chỉ khi chúng có hai vectơ pháp tuyến vuông góc. Do đó:
• Nếu ∆1 và ∆2 lần lượt có phương trình a1x + b1y + c1 = 0 và a2x + b2y + c2 = 0 thì ta có:
(∆1, ∆2) = 90° ⇔ a1a2 + b1b2 = 0.
• Nếu ∆1 và ∆2 lần lượt có phương trình y = k1x + m1 và y = k2x + m2 thì ta có:
(∆1, ∆2) = 90° ⇔ k1k2 = –1.
Nói cách khác, hai đường thẳng có tích các hệ số góc bằng –1 thì vuông góc với nhau.
Ví dụ: Tìm số đo của góc giữa hai đường thẳng d1 và d2 trong các trường hợp sau:
a) d1: x – 2y + 5 = 0 và d2: 3x – y = 0.
b) d1: 4x + 3y – 21 = 0 và d2:
c) d1: và d2:
Hướng dẫn giải
a) d1: x – 2y + 5 = 0 và d2: 3x – y = 0
d1, d2 có vectơ pháp tuyến lần lượt là .
Ta có .
Suy ra (d1, d2) = 45°.
Vậy (d1, d2) = 45°.
b) d1: 4x + 3y – 21 = 0 và d2:
d1 có vectơ pháp tuyến .
d2 có vectơ chỉ phương nên có vectơ pháp tuyến .
Ta có .
Suy ra // .
Vậy (d1, d2) = 0°.
c) d1: và d2:
d1, d2 có vectơ chỉ phương lần lượt là .
Ta có (–1).(–4) + 2.(–2) = 0.
Suy ra
Vậy (d1, d2) = 90°.
4. Khoảng cách từ một điểm đến một đường thẳng
Trong mặt phẳng Oxy, cho đường thẳng ∆ có phương trình ax + by + c = 0 (a2 + b2 > 0) và điểm M0(x0; y0). Khoảng cách từ điểm M0 đến đường thẳng ∆, kí hiệu là d(M0, ∆), được tính bởi công thức: .
Ví dụ: Tính khoảng cách từ điểm đến đường thẳng được cho tương ứng như sau:
a) A(3; 4) và ∆: 4x + 3y + 1 = 0.
b) B(1; 2) và d: 3x – 4y + 1 = 0.
Hướng dẫn giải
a) Với A(3; 4) và ∆: 4x + 3y + 1 = 0 ta có:
.
Vậy khoảng cách từ điểm A đến đường thẳng ∆ bằng 5.
b) Với B(1; 2) và d: 3x – 4y + 1 = 0 ta có:
.
Vậy khoảng cách từ điểm B đến đường thẳng d bằng .