Vận dụng 3 trang 51 Toán 10 Tập 2 | Chân trời sáng tạo Giải Toán lớp 10

Vận dụng 3 trang 51 Toán 10 Tập 2 | Chân trời sáng tạo Giải Toán lớp 10

Nguyễn Thị Thuỳ Linh Ngày: 07-04-2023 Lớp 10

3 K

Với giải Vận dụng 3 trang 51 Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 2: Đường thẳng trong mặt phẳng tọa độ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 2: Đường thẳng trong mặt phẳng tọa độ

Vận dụng 3 trang 51 Toán lớp 10: Một người bắt đầu mở một vòi nước. Nước từ vòi chảy với vận tốc là 2 $m^{3} / h$ vào một cái bể đã chứa sẵn 5 $m^{3}$ nước.

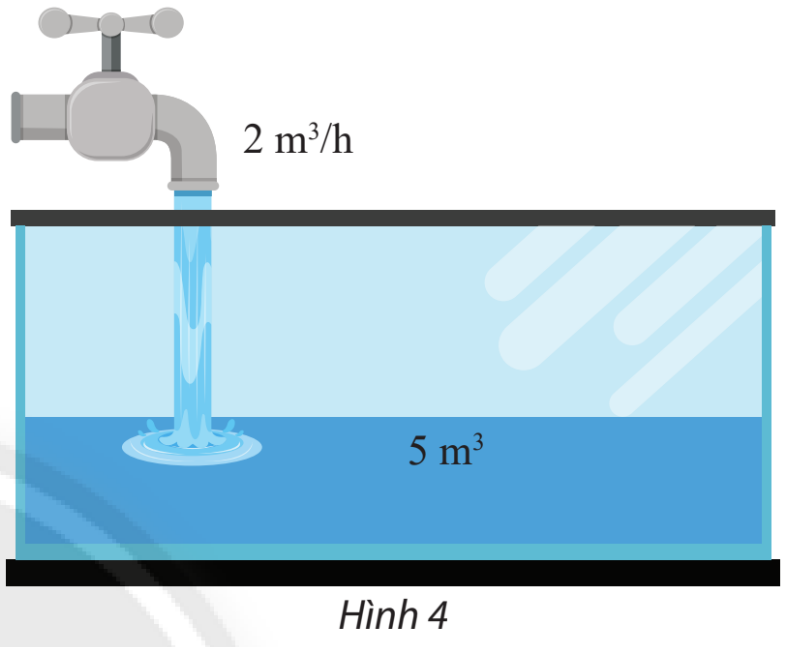
Vận dụng 3 trang 51 Toán lớp 10 Tập 2 | Chân trời sáng tạo (ảnh 1)

a) Viết biểu thức tính thể tích y của nước có trong bể sau x giờ

b) Gọi $y = f (x)$ là hàm số xác định được từ câu a). Vẽ đồ thị d của hàm số này

c) Viết phương trình tham số và phương trình tổng quát của đường thẳng d

Lời giải:

a) Thể tích nước trong bể được tính bằng công thức $y = 5 + 2 x$

b)

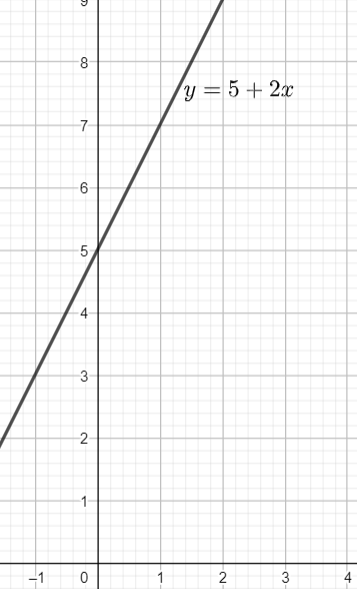
Vận dụng 3 trang 51 Toán lớp 10 Tập 2 | Chân trời sáng tạo (ảnh 2)

c) Ta có đồ thị hàm số bậc nhất $y = 5 + 2 x \Leftrightarrow 2 x - y + 5 = 0$

Vậy phương trình tổng quát của đường thẳng d là $2 x - y + 5 = 0$

Từ phương trình tổng quát ta có vectơ pháp tuyến $\vec{n} = (2; - 1)$ , từ đó ta có vectơ chỉ phương $\vec{u} = (1; 2)$

Khi $x = 0$ thì $y = 5$ nên đường thẳng đó đi qua điểm $(0; 5)$

Ta có phương trình tham số của đường thẳng d là ${\begin{cases} x = t \\ y = 5 + 2 t \end{cases}$

Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Khởi động trang 46 Toán lớp 10:...

Khám phá 1 trang 46 Toán lớp 10: Trong mặt phẳng Oxy, cho hai đường thẳng $Δ$ đi qua điểm $M_{0} (x_{0}; y_{0})$ và vectơ $\vec{n} = (a; b)$ và $\vec{u} = (b; - a)$ khác vectơ 0. Cho biết $\vec{u}$ có giá song song hoặc trùng với $Δ$ ...

Khám phá 2 trang 47 Toán lớp 10: Trong mặt phẳng Oxy, cho đường thẳng $Δ$ đi qua điểm $M_{0} (x_{0}; y_{0})$ và nhận $\vec{u} = (u_{1}; u_{2})$ là vectơ chỉ phương. Với mỗi điểm $M (x; y)$ thuộc $Δ$ , tìm tọa độ của điểm M theo tọa độ của $M_{0}$ và $\vec{u}$ ...

Thực hành 1 trang 47 Toán lớp 10: a) Viết phương trình tham số của đường thẳng d đi qua điểm $B (- 9; 5)$ và nhận $\vec{v} = (8; - 4)$ là vectơ chỉ phương...

Vận dụng 1 trang 48 Toán lớp 10: Một trò chơi đua xe ô tô vượt da mặt trên máy tính là xác định trước một hệ trục tọa độ Oxy. Cho biết một ô tô chuyển động thẳng đều từ điểm $M (1; 1)$ với Vectơ vận tốc $\vec{v} = (40; 30)$ ...

Khám phá 3 trang 48 Toán lớp 10: Trong mặt phẳng Oxy, cho đường thẳng $Δ$ đi qua điểm $M_{0} (x_{0}; y_{0})$ và nhận $\vec{n} = (a; b)$ làm vectơ pháp tuyến. Với mỗi điểm $M (x; y)$ thuộc $Δ$ , chứng tỏ rằng điểm $M (x; y)$ có tọa độ thỏa mãn phương trình:...

Thực hành 2 trang 49 Toán lớp 10: Viết phương trình tham số và phương trình tổng quát của đường thẳng $Δ$ trong các trường hợp sau:...

Vận dụng 2 trang 49 Toán lớp 10: Một người đã lập trình một trò chơi trên máy tính. Trên màn hình máy tính đã xác định trước một hệ trục tọa độ Oxy. Người đó viết lệnh để một điểm $M (x; y)$ từ vị trí $A (1; 2)$ chuyển động thẳng đều với Vectơ vận tốc $\vec{v} = (3; - 4)$ ...

Thực hành 3 trang 51 Toán lớp 10: Tìm các hàm số bậc nhất có đồ thị là các đường thẳng trong thực hành 2...

Khám phá 4 trang 51 Toán lớp 10: Cho hai đường thẳng $Δ_{1}$ và $Δ_{2}$ một vectơ pháp tuyến lần lượt là $\vec{n_{1}}$ và $\vec{n_{2}}$ ...

Thực hành 4 trang 53 Toán lớp 10: Xét vị trí tương đối của các cặp đường thẳng $d_{1}$ và $d_{2}$ trong các trường hợp sau:...

Vận dụng 4 trang 53 Toán lớp 10: Viết phương trình đường thẳng $d_{1}$ :...

Khám phá 5 trang 54 Toán lớp 10: Cho hai đường thẳng xy và zt cắt nhau tại O và cho biết $\hat{x O z} = 38^{\circ}$ (hình 6)...

Khám phá 6 trang 54 Toán lớp 10: Cho hai đường thẳng...

Thực hành 5 trang 56 Toán lớp 10: Tìm số đo của góc giữa hai đường thẳng $Δ_{1}$ và $Δ_{2}$ trong các trường hợp sau...

Vận dụng 5 trang 56 Toán lớp 10: Tìm số đo của góc giữa hai đường thẳng là đồ thị của hai hàm số $y = x$ và $y = 2 x + 1$ ...

Khám phá 7 trang 56 Toán lớp 10: Trong mặt phẳng Oxy. Cho đường thẳng $Δ : a x + b y + c = 0 (a^{2} + b^{2} > 0)$ có vectơ pháp tuyến $\vec{n}$ và cho điểm $M_{0} (x_{0}; y_{0})$ có hình chiếu vuông góc $H (x_{H}; y_{H})$ trên $Δ$ (hình 9)...

Thực hành 6 trang 57 Toán lớp 10: Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ các đỉnh là $A (1; 1), B (5; 2), C (4; 4)$ . Tính độ dài các đường cao của tam giác ABC...

Vận dụng 6 trang 57 Toán lớp 10: Tính khoảng cách giữa hai đường thẳng $d_{1} : 4 x - 3 y + 2 = 0$ và $d_{2} : 4 x - 3 y + 12 = 0$ ...

Bài 1 trang 57 Toán lớp 10: Lập phương trình tham số và phương trình tổng quát của đường thẳng d trong mỗi trường hợp sau:...

Bài 2 trang 57 Toán lớp 10: Cho tam giác ABC biết $A (2; 5), B (1; 2)$ và $C (5; 4)$ ...

Bài 3 trang 57 Toán lớp 10: Lập phương trình tham số và phương trình tổng quát của đường thẳng $Δ$ trong mỗi trường hợp sau:...

Bài 4 trang 57 Toán lớp 10: Xét vị trí tương đối của cặp đường thẳng $d_{1}$ và $d_{2}$ sau đây:...

Bài 5 trang 58 Toán lớp 10: Cho đường thẳng d có phương trình tham số ${\begin{cases} x = 2 - t \\ y = 5 + 3 t \end{cases}$ ...

Bài 6 trang 58 Toán lớp 10: Tìm số đo của góc giữa hai đường thẳng $d_{1}$ và $d_{2}$ trong các trường hợp sau:...

Bài 7 trang 58 Toán lớp 10: Tính khoảng cách từ điểm M đến đường thẳng $Δ$ trong các trường hợp sau:...

Bài 8 trang 58 Toán lớp 10: Tính khoảng cách giữa hai đường thẳng $Δ : 3 x + 4 y - 10 = 0$ và $Δ^{'} : 6 x + 8 y - 1 = 0$ ...

Bài 9 trang 58 Toán lớp 10: Trong mặt phẳng Oxy cho điểm $S (x; y)$ di động trên đường thẳng $d : 12 x - 5 y + 16 = 0$ . Tính khoảng cách ngắn nhất từ điểm $M (5; 10)$ đến điểm S...

Bài 10 trang 58 Toán lớp 10: Một người đang viết chương trình cho trò chơi đá bóng robot. Gọi $A (- 1; 1), B (9; 6), C (5; - 3)$ là 3 vị trí trên màn hình...

Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Toạ độ của vecto

Bài 2: Đường thẳng trong mặt phẳng tọa độ

Bài 3: Đường tròn trong mặt phẳng tọa độ

Bài 4: Ba đường conic trong mặt phẳng tọa độ

Bài 1: Không gian mẫu và biến cố

Từ khóa :

toán 10 Giải bài tập đường thẳng Mặt phẳng tọa độ đường thẳng

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

169

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

143

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

116

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.