Với giải sách bài tập Toán 10 Bài 1: Hàm số và đồ thị sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài 1: Hàm số và đồ thị

Giải SBT Toán 10 trang 45 Tập 1

Bài 1 trang 45 SBT Toán 10 Tập 1: Tập xác định của các hàm số sau:

a) f(x) = $\frac{4x-1}{\sqrt{2x-5}}$;

b) f(x) = $\frac{2-x}{\left(x+3\right)\left(x-7\right)}$;

c) $f\left(x\right)=\left\{\begin{array}{l}\frac{1}{x-3}khix\ge 0\\ 1khix<0\end{array}\right.$.

Lời giải:

a) Biểu thức $\frac{4x-1}{\sqrt{2x-5}}$ có nghĩa khi 2x – 5 > 0 hay x > $\frac{5}{2}$.

Vậy tập xác định của hàm số là D = $\left(\frac{5}{2};+\infty \right)$.

b) Biểu thức $\frac{2-x}{\left(x+3\right)\left(x-7\right)}$ có nghĩa khi (x + 3)(x – 7) ≠ 0 ⇒ x ≠ – 3 và x ≠ 7.

Vậy tập xác định của hàm số là D = ℝ \ {– 3; 7}.

c) Hàm số lấy giá trị bằng 1 khi x < 0 nên hàm số xác định với mọi x < 0.

Khi x ≥ 0, hàm số xác định khi và chỉ khi x – 3 ≠ 0 ⇒ x ≠ 3.

Vậy tập xác định của hàm số là D = ℝ \ {3}.

Bài 2 trang 45 SBT Toán 10 Tập 1: Vẽ đồ thị các hàm số sau:

a) $f\left(x\right)=\left\{\begin{array}{l}{x}^{2}khix\le 2\\ x+2khix>2;\end{array}\right.$

b) f(x) = |x + 3| – 2. 

Lời giải:

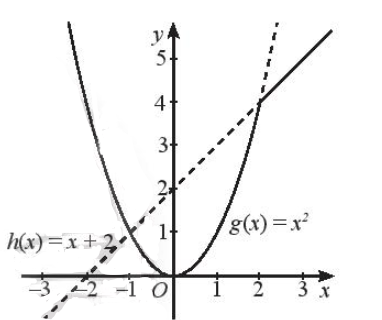
a) + Vẽ đồ thị hàm số g(x) = x² và giữ lại phần đồ thị ứng với x ≤ 2:

Đồ thị hàm số g(x) = x² là một parabol có đỉnh là gốc tọa độ O, trục đối xứng là trục Oy, đồ thị có bề lõm hướng lên trên, đi qua các điểm (1; 1), (– 1; 1), (2; 4), (– 2; 4).

Ta giữ lại phần đồ thị nằm bên trái đường thẳng x = 2:

+ Vẽ đồ thị hàm số h(x) = x + 2 và giữ lại phần đồ thị ứng với x > 2.

Đồ thị hàm số h(x) = x + 2 là một đường thẳng đi qua hai điểm (0; 2) và (– 2; 0).

Ta giữ lại phần đường thẳng nằm bên phải đường thẳng x = 2.

Ta được đồ thị cần vẽ như hình sau:

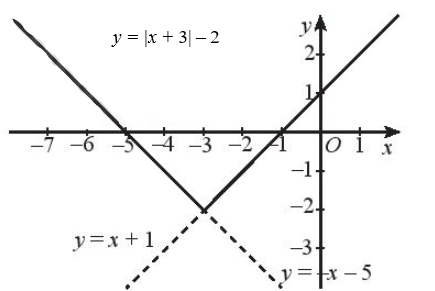
b) Với x + 3 ≥ 0 ⇔ x ≥ – 3, ta có: |x + 3| – 2 = x + 3 – 2 = x + 1.

Với x + 3 < 0 ⇔ x < – 3, ta có: |x + 3| – 2 = – (x + 3) – 2 = – x – 3 – 2 = – x – 5.

Khi đó ta có: $f\left(x\right)=\left\{\begin{array}{l}x+1khix\ge -3\\ -x-5khix<-3\end{array}\right.$.

Ta vẽ đồ thị hàm số g(x) = x + 1 và giữ lại phần đồ thị ứng với x ≥ – 3: Đồ thị hàm số g(x) = x + 1 là đường thẳng đi qua hai điểm (0; 1) và (– 1; 0).

Ta vẽ đồ thị hàm số h(x) = – x – 5 và giữ lại phần đồ thị ứng với x < – 3: Đồ thị hàm số h(x) = – x – 5 là đường thẳng đi qua hai điểm (– 5; 0) và (– 3; – 2).

Ta được đồ thị của hàm số cần vẽ như hình sau:

Giải SBT Toán 10 trang 46 Tập 1

Bài 3 trang 46 SBT Toán 10 Tập 1: Trong kinh tế thị trường, lượng cầu và lượng cung là hai khái niệm quan trọng. Lượng cầu chỉ khả năng về số lượng sản phẩm cần mua của bên mua (người dùng), tùy theo đơn giá bán sản phẩm; còn lượng cung chỉ khả năng cung cấp số lượng sản phẩm này cho thị trường của bên bán (nhà sản xuất) cũng phụ thuộc vào đơn giá sản phẩm.

Người ta khảo sát nhu cầu của thị trường đối với sản phẩm A theo đơn giá của sản phẩm này và thu được bảng sau:

a) Hãy cho biết tại sao bảng giá trị trên xác định một hàm số? Hãy tìm tập xác định và tập giá trị của hàm số đó (gọi là hàm cầu).

b) Giả sử lượng cung của sản phẩm A tuân theo công thức $y=f\left(x\right)=\frac{x^2}{50}$, trong đó x là đơn giá sản phẩm A và y là lượng cung ứng với đơn giá này. Hãy điền các giá trị của hàm số f(x) (gọi là hàm cung) vào bảng sau:

 c) Ta nói thị trường của một sản phẩm là cân bằng khi lượng cung và lượng cầu bằng nhau. Hãy tìm đơn giá x của sản phẩm A khi thị trường cân bằng.

Lời giải:

a) Từ bảng đã cho ta có thể thấy với mỗi mức đơn giá, đều có duy nhất một giá trị về lượng cầu. Do vậy bảng giá trị cho ở đề bài xác định một hàm số.

Hàm số này có tập xác định D = {10; 20; 40; 70; 90} và có tập giá trị T = {338; 288; 200; 98; 50}.

b) Ta có hàm cung: $y=f\left(x\right)=\frac{x^2}{50}$.

Với x = 10 thì $y=f\left(10\right)=\frac{{10}^2}{50}=2$;

Với x = 20 thì $y=f\left(20\right)=\frac{{20}^2}{50}=8$;

Với x = 40 thì $y=f\left(40\right)=\frac{{40}^2}{50}=32$;

Với x = 70 thì $y=f\left(70\right)=\frac{{70}^2}{50}=98$;

Với x = 90 thì $y=f\left(90\right)=\frac{{90}^2}{50}=162$;

Vậy ta điền được bảng sau:

 c) Từ hai bảng giá trị của lượng cung và lượng cầu, ta tìm được giá trị x = 70 thì lượng cung và lượng cầu đều bằng 98.

Vậy thị trường của sản phẩm A cân bằng khi đơn giá của sản phẩm A là 70 000 (đồng).

Bài 4 trang 46 SBT Toán 10 Tập 1: Tìm khoảng đồng biến, nghịch biến của các hàm số sau:

a) $f\left(x\right)=\frac{1}{-x-5}$;

b) f(x) = |3x – 1|.

Lời giải:

a) Tập xác định của hàm số là: D = ℝ \ {– 5}.

+ Xét khoảng (– ∞; – 5):

Lấy hai số x₁, x₂ tùy ý thuộc (– ∞; – 5) sao cho x₁ < x₂.

Ta có: $f\left(x_1\right)-f\left(x_2\right)=\frac{1}{-x_1-5}-\frac{1}{-x_2-5}$$=\frac{-x_2-5-\left(-x_1-5\right)}{\left(-x_1-5\right)\left(-x_2-5\right)}$$=\frac{x_1-x_2}{\left(x_1+5\right)\left(x_2+5\right)}$.

Vì x₁, x₂ ∈ (– ∞; – 5) nên x₁ + 5 < 0 và x₂ + 5 < 0.

Lại có: x₁ < x₂ nên x₁ – x₂ < 0.

Do đó, f(x₁) – f(x₂) $=\frac{x_1-x_2}{\left(x_1+5\right)\left(x_2+5\right)}$ < 0 hay f(x₁) < f(x₂).

Vậy hàm số đồng biến trên khoảng (– ∞; – 5). (1)

+ Xét khoảng (– 5; + ∞):

Lấy hai số x₃, x₄ tùy ý thuộc (– 5; + ∞) sao cho x₃ < x₄.

Ta có: $f\left(x_3\right)-f\left(x_4\right)=\frac{1}{-x_3-5}-\frac{1}{-x_4-5}$$=\frac{-x_4-5-\left(-x_3-5\right)}{\left(-x_3-5\right)\left(-x_4-5\right)}$$=\frac{x_3-x_4}{\left(x_3+5\right)\left(x_4+5\right)}$.

Vì x₃, x₄ ∈ (– 5; + ∞) nên x₃ + 5 > 0 và x₄ + 5 > 0.

Lại có: x₃ < x₄ nên x₃ – x₄ < 0.

Do đó, f(x₃) – f(x₄) $=\frac{x_3-x_4}{\left(x_3+5\right)\left(x_4+5\right)}$ < 0 hay f(x₁) < f(x₂).

Vậy hàm số đồng biến trên khoảng (– 5; + ∞). (2)

Từ (1) và (2) suy ra hàm số đã cho đồng biến trên các khoảng (– ∞; – 5) và (– 5; + ∞).

b) Với 3x – 1 ≥ 0 hay x ≥ $\frac{1}{3}$, ta có: |3x – 1| = 3x – 1.

Với 3x – 1 < 0 hay x < $\frac{1}{3}$, ta có: |3x – 1| = – (3x – 1) = – 3x + 1.

Khi đó ta có: $f\left(x\right)=\left\{\begin{array}{l}3x-1khix\ge \frac{1}{3}\\ -3x+1khix<\frac{1}{3}\end{array}\right.$.

Ta xét sự đồng biến, nghịch biến của hàm số g(x) = 3x – 1 trên khoảng $\left(\frac{1}{3};+\infty \right)$ và của hàm số h(x) = – 3x + 1 trên khoảng $\left(-\infty ;\frac{1}{3}\right)$.

+ Lấy hai số x₁, x₂ tùy ý thuộc khoảng $\left(\frac{1}{3};+\infty \right)$ sao cho x₁ < x­₂:

Ta có: f(x₁) – f(x₂) = (3x₁ – 1) – (3x₂ – 1) = 3(x₁ – x₂) < 0 (do x₁ < x₂ nên x₁ – x₂ < 0).

Suy ra f(x₁) < f(x₂).

Vậy hàm số g(x) đồng biến trên $\left(\frac{1}{3};+\infty \right)$ hay f(x) đồng biến trên $\left(\frac{1}{3};+\infty \right)$. (1)

+ Lấy hai số x₃, x₄ tùy ý thuộc khoảng $\left(-\infty ;\frac{1}{3}\right)$ sao cho x₃ < x₄:

Ta có: f(x₃) – f(x₄) = (– 3x₃ + 1) – (– 3x₄ + 1) = 3(x₄ – x₃) > 0 (do x₃ < x₄ nên x₄ – x₃ > 0).

Suy ra f(x₃) > f(x₄).

Vậy hàm số h(x) nghịch biến trên $\left(-\infty ;\frac{1}{3}\right)$ hay f(x) nghịch biến khoảng $\left(-\infty ;\frac{1}{3}\right)$. (2)

Từ (1) và (2) suy ra hàm số f(x) nghịch biến trên khoảng $\left(-\infty ;\frac{1}{3}\right)$ và đồng biến trên khoảng $\left(\frac{1}{3};+\infty \right)$.

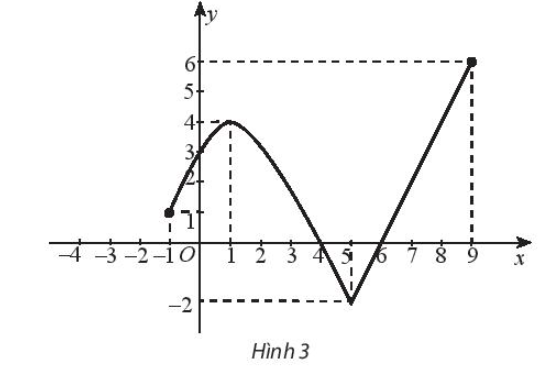
Bài 5 trang 46 SBT Toán 10 Tập 1: Tìm khoảng đồng biến, nghịch biến của hàm số có đồ thị như sau:

Lời giải:

Quan sát Hình 3 ta thấy:

- Đồ thị hàm số có dạng đi lên từ điểm có tọa độ (– 1; 1) đến điểm có tọa độ (1; 4) nên hàm số đồng biến trên khoảng (– 1; 1);

- Đồ thị hàm số có dạng đi xuống từ điểm có tọa độ (1; 4) đến điểm có tọa độ (5; – 2) nên hàm số nghịch biến trên khoảng (1; 5);

- Đồ thị hàm số có dạng đi lên từ điểm có tọa độ (5; – 2) đến điểm có tọa độ (9; 6) nên hàm số đồng biến trên khoảng (5; 9).

Vậy hàm số có đồ thị như Hình 3 đồng biến trên các khoảng (– 1; 1) và (5; 9), nghịch biến trên khoảng (1; 5).

Giải SBT Toán 10 trang 47 Tập 1

Bài 6 trang 47 SBT Toán 10 Tập 1: Vẽ đồ thị hàm số sau:

$f\left(x\right)=\left\{\begin{array}{l}-x+1khix<-1\\ 1khi-1\le x<1\\ x^{2}khix\ge 1.\end{array}\right.$

Lời giải:

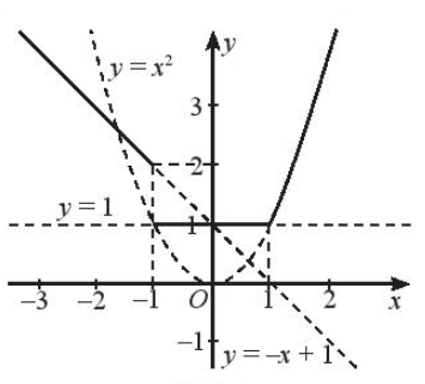
Ta vẽ đồ thị hàm số g(x) = – x + 1 trên khoảng (– ∞; – 1), đồ thị hàm số h(x) = 1 trên nửa khoảng [– 1; 1), đồ thị hàm số k(x) = x² trên nửa khoảng [1; + ∞).

Khi đó ta có đồ thị hàm số f(x) như sau:

Bài 7 trang 47 SBT Toán 10 Tập 1: Trong các đường biểu diễn được cho trong Hình 4, chỉ ra trường hợp không phải là đồ thị hàm số và giải thích tại sao?

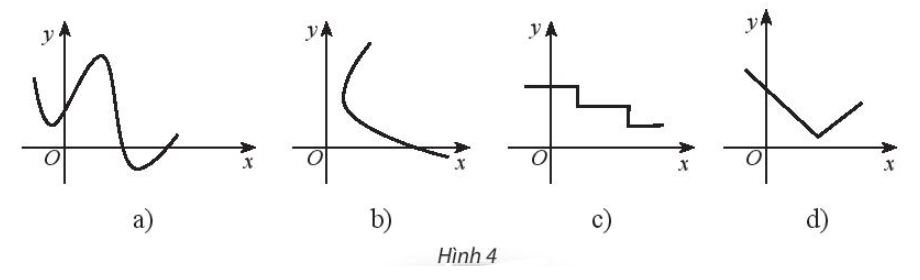
Lời giải:

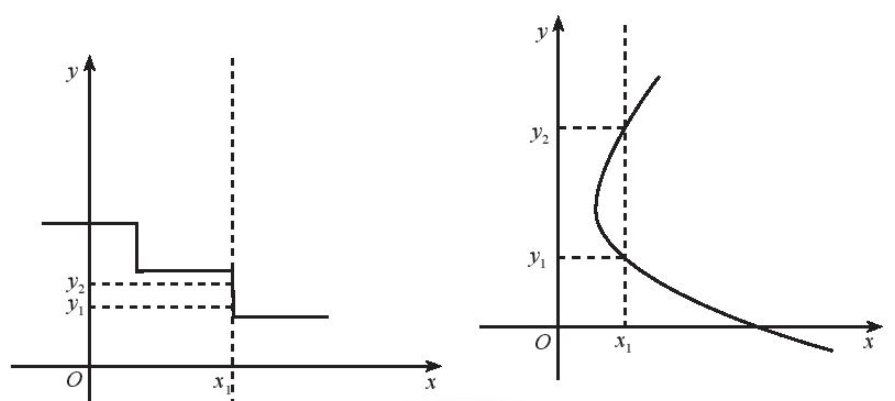
Hai đường biểu diễn ở Hình b và Hình c không phải là đồ thị hàm số vì ứng với một giá trị của x, có đến hai (hay nhiều) giá trị khác nhau của y (quan sát trên hình sau).

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 2

Bài 2: Hàm số bậc hai

Bài tập cuối chương 3

Bài 1: Giá trị lượng giác của một góc từ 0 đến 180

Lý thuyết Hàm số và đồ thị

1. Hàm số. Tập xác định và tập giá trị của hàm số

- Giả sử x và y là hai đại lượng biến thiên và x nhận giá trị thuộc tập số D.

Nếu với mỗi giá trị x thuộc D, ta xác định được một và chỉ một giá trị tương ứng y thuộc tập hợp số thực ℝ thì ta có một hàm số.

Ta gọi x là biến số và y là hàm số của x.

Tập hợp D được gọi là tập xác định của hàm số.

Tập hợp T gồm tất cả các giá trị y (tương ứng với x thuộc D) gọi là tập giá trị của hàm số.

Chú ý:

+ Ta thường dùng kí hiệu f(x) để chỉ giá trị y tương ứng với x, nên hàm số còn được viết là y = f(x).

+ Khi một hàm số được cho bằng công thức mà không chỉ rõ tập xác định thì ta quy ước:

Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

+ Một hàm số có thể được cho bởi hai hay nhiều công thức.

Ví dụ:

+ Hàm số có thể được cho bằng bảng dưới đây:

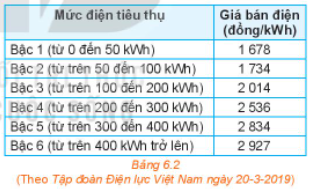
Với mỗi lượng điện tiêu thụ (kWh) thì sẽ có một số tiền phải trả tương ứng (nghìn đồng). Ta nói bảng trên biểu thị một hàm số.

+ Hàm số có thể được cho bằng công thức, ví dụ như: y = 2x – 1, y = x²,  …. với biến số là x và y là hàm số của x.

+ Hàm số được cho bởi hai công thức như $f\left(x\right)=\left\{\begin{array}{l}-2x+1 khi x\le -3\\ \frac{x+7}{2} khi x>-3 \end{array}\right..$  Nghĩa là với x ≤ ‒3 thì f(x) = ‒2x + 1, với x > ‒3 thì $f\left(x\right)=\frac{x+7}{2}$  

+ Với hàm số y = f(x) = $\frac{x+1}{x-2}$ , tập xác định của hàm số là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa tức là $\frac{x+1}{x-2}$ có nghĩa, hay x ≠ 2.

Vậy tập xác định của hàm số này là D = ℝ\{2}.

2. Đồ thị hàm số

- Cho hàm số y = f(x) có tập xác định D.

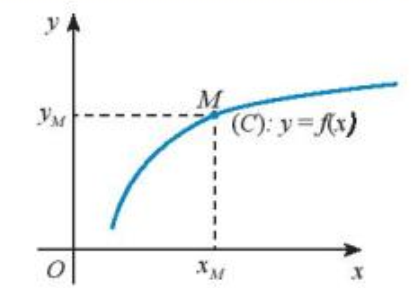
Trên mặt phẳng tọa độ Oxy, đồ thị (C) của hàm số là tập hợp tất cả các điểm M(x; y) với x ∈ D và y = f(x).

Chú ý: Điểm M(x_M; y_M) thuộc đồ thị hàm số y = f(x) khi và chỉ khi x_M ∈ D và y_M = f(x_M).

Ví dụ:

+ Cho hàm số y = f(x) = 2x – 1 có tập xác định D = ℝ.

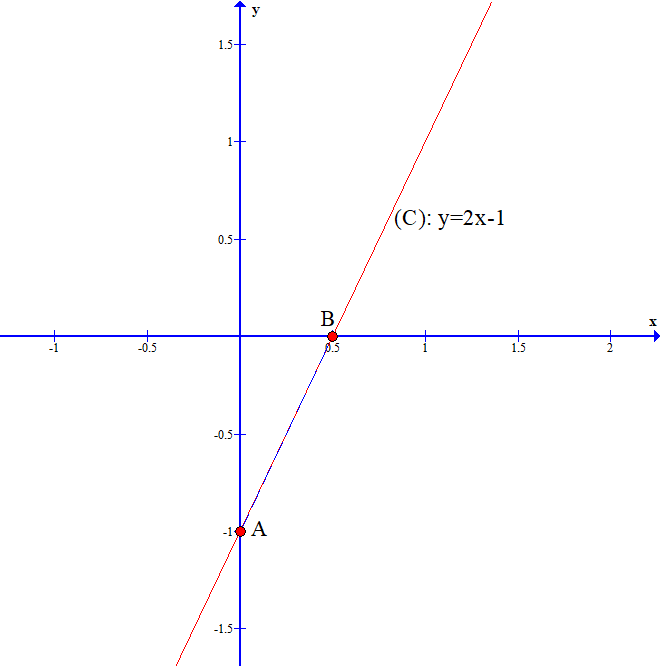
Trên mặt phẳng tọa độ Oxy, đồ thị (C) là đồ thị của hàm số y = f(x) = 2x – 1.

Khi thay x = 0 và y = ‒1 vào hàm số, ta được ‒1 = 2. 0 – 1 là mệnh đề đúng nên điểm A(0; ‒1) là điểm thuộc đồ thị (C).

Khi thay x = 0,5 và y = 0 vào hàm số, ta được 0 = 2. 0,5 – 1 là mệnh đề đúng nên điểm B(0,5; 0) là điểm thuộc đồ thị (C).

3. Hàm số đồng biến, hàm số nghịch biến

- Với hàm số y = f(x) xác định trên khoảng (a; b), ta nói:

+ Hàm số đồng biến trên khoảng (a; b) nếu

∀x₁, x₂ ∈ (a; b), x₁ < x₂ ⇒ f(x₁) < f(x₂).

+ Hàm số nghịch biến trên khoảng (a; b) nếu

∀x₁, x₂ ∈ (a; b), x₁ < x₂ ⇒ f(x₁) > f(x₂).

Nhận xét:

+ Khi hàm số đồng biến (tăng) trên khoảng (a; b) thì đồ thị của nó có dạng đi lên từ trái sang phải. Ngược lại, khi hàm số nghịch biến (giảm) trên khoảng (a; b) thì đồ thị của nó có dạng đi xuống từ trái sang phải.

Ví dụ:

+ Cho hàm số y = f(x) = 2x – 1 xác định trên ℝ.

Xét hai giá trị x₁ = 1 và x₂ = 2 đều thuộc ℝ, ta có:

f(x₁) = f(1) = 2.1 – 1 = 1.

f(x₂) = f(2) = 2.2 – 1 = 3.

Ta thấy x₁ < x₂ và f(x₁) < f(x₂) nên hàm số y = f(x) = 2x – 1 là hàm số đồng biến trên ℝ.

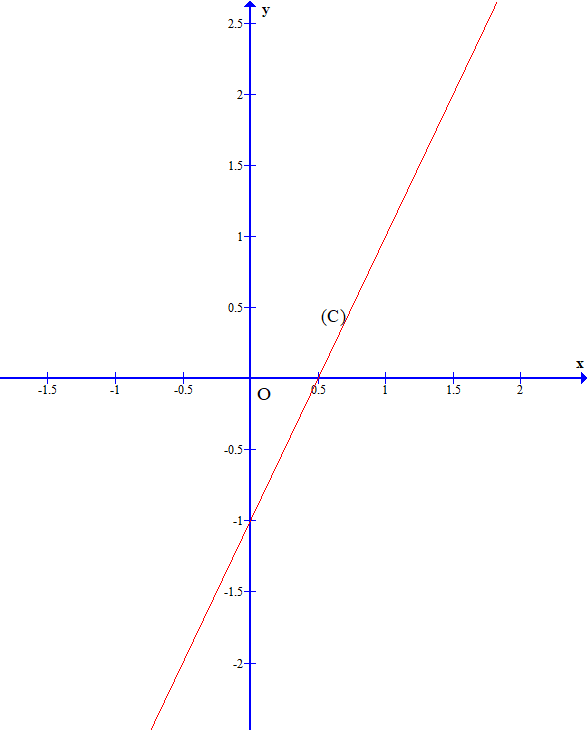
Ta thấy hàm số y = f(x) = 2x – 1 là hàm số đồng biến trên ℝ nên đồ thị của nó có dạng đi lên từ trái sang phải.

+ Cho hàm số y = f(x) = ‒ x + 2 xác định trên ℝ.

Xét 2 giá trị x₁ = 1 và x₂ = 2 đều thuộc ℝ, ta có:

f(x₁) = f(1) = ‒1 + 2 = 1.

f(x₂) = f(2) = ‒ 2 + 2 = 0.

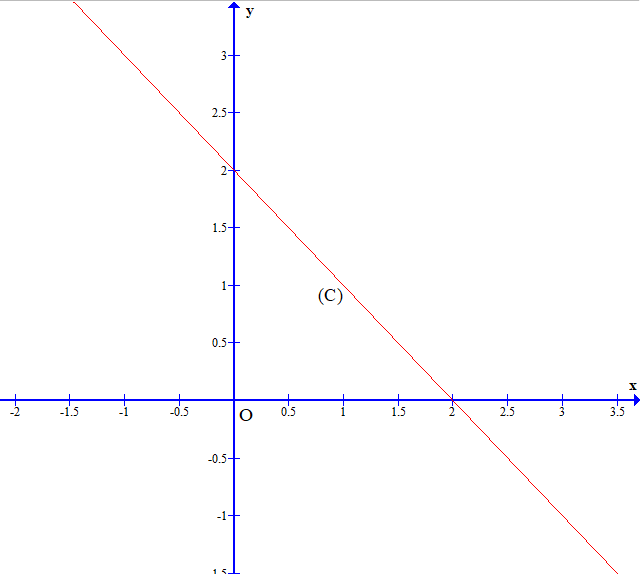
Ta thấy x₁ < x₂ và f(x₁) > f(x₂) nên hàm số y = f(x) = ‒ x + 2 là hàm số nghịch biến trên ℝ.

Ta thấy hàm số y = f(x) = ‒ x + 2 là hàm số nghịch biến trên ℝ nên đồ thị của nó có dạng đi xuống từ trái sang phải.

Ví dụ: Cho hàm số y = f(x) có tập xác định là [‒3; 3] và có đồ thị hàm số như hình vẽ.

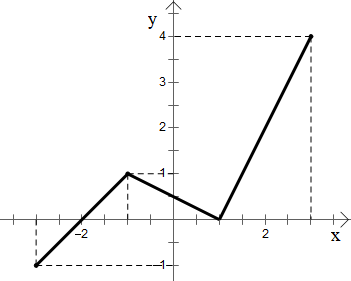
Tìm khoảng đồng biến, nghịch biến của hàm số trên.

Hướng dẫn giải

Dựa vào đồ thị nhận thấy:

- Đồ thị hàm số có dạng đi lên từ trái sang phải trên các khoảng (‒3; ‒1) và (1; 3) nên hàm số đồng biến trên khoảng (‒3; ‒1) và (1; 3);

- Đồ thị hàm số có dạng đi xuống từ trái sang phải trên khoảng (‒1; 1) nên hàm số nghịch biến trên khoảng (‒1; 1).