Giải SGK Toán 10 Bài 4 (Cánh diều): Tổng và hiệu của hai vectơ

Nguyễn Thị Thuỳ Linh Ngày: 24-08-2024 Lớp 10

14.4 K

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 4: Tổng và hiệu của hai vectơ chi tiết sách Toán 10 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 4: Tổng và hiệu của hai vectơ

Giải Toán 10 trang 83 Tập 1

Câu hỏi khởi động trang 83 Toán lớp 10: Quan sát hình ảnh hai người cùng kéo một chiếc thuyền theo hai hướng khác nhau (Hình 48). Tuy nhiên, chiếc thuyền lại không di chuyển theo cùng hướng với một trong hai người đó mà di chuyển theo hướng khác.

Quan sát hình ảnh hai người cùng kéo một chiếc thuyền theo hai hướng khác nhau

Tại sao chiếc thuyền lại di chuyển như vậy?

Lời giải:

Chiếc thuyền di chuyển theo hướng hợp lực của hai người. Chi tiết xem Luyện tập 2 trang 84.

1. Tổng của hai vectơ

Hoạt động 1 trang 83 Toán lớp 10: Một vật dịch chuyển từ A đến B và tiếp tục dịch chuyển từ B đến C (Hình 49).

Một vật dịch chuyển từ A đến B và tiếp tục dịch chuyển từ B đến C (Hình 49)

a) Biểu diễn vectơ dịch chuyển của vật từ A đến B và từ B đến C.

b) Xác định vectơ dịch chuyển tổng hợp của vật.

Lời giải:

a) Vật dịch chuyển từ A đến B theo vectơ $\vec{A B}$ , vật dịch chuyển từ B đến C theo vectơ $\vec{B C}$ .

b) Vật di chuyển từ A đến B và từ B đến C, nghĩa là điểm đầu đường đi của vật là A và điểm cuối đường đi là C, do đó vectơ dịch chuyển tổng hợp của vật là vectơ $\vec{A C}$ .

Hoạt động 2 trang 83 Toán lớp 10: Cho hai vectơ $\vec{a}, \vec{b}$ . Lấy một điểm A tùy ý.

a) Vẽ $\vec{A B} = \vec{a}, \vec{B C} = \vec{b}$ (Hình 50).

b) Tổng của hai vectơ $\vec{a}$ và $\vec{b}$ bằng vectơ nào?

Lời giải:

a) Lấy điểm A bất kì, qua A vẽ đường thẳng song song với giá của vectơ $\vec{a}$ , trên đường thẳng này về phía cùng hướng với vectơ $\vec{a}$ , lấy điểm B sao cho $|\vec{A B}| = |\vec{a}|$ .

Qua điểm B, vẽ đường thẳng song song với giá của vectơ $\vec{b}$ , trên đường thẳng này về phía cùng hướng với vectơ $\vec{b}$ , lấy điểm C sao cho $|\vec{B C}| = |\vec{b}|$ .

Vậy ta có $\vec{A B} = \vec{a}, \vec{B C} = \vec{b}$ .

Cho hai vectơ a, b . Lấy một điểm A tùy ý. Vẽ vectơ AB = vectơ a, vectơ BC= vectơ b (Hình 50).

b) Tổng của hai vectơ $\vec{a}$ và $\vec{b}$ bằng vectơ $\vec{A C}$

Giải Toán 10 trang 84 Tập 1

Luyện tập 1 trang 84 Toán lớp 10: Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh $\vec{P B} + \vec{M C} = \vec{A N}$ .

Lời giải:

Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh vectơ PB + vectơ MC = vectơ AN

Ta có: M là trung điểm của BC nên $\vec{B M} = \vec{M C}$

Khi đó: $\vec{P B} + \vec{M C} = \vec{P B} + \vec{B M} = \vec{P M}$ (1).

Lại có P, M lần lượt là trung điểm của AB và BC nên PM là đường trung bình của tam giác ABC nên PM // = $\frac{1}{2}$ AC.

Mà $A N = \frac{1}{2} A C$ (do N là trung điểm của AC)

Nên PM // AN và PM = AN.

Khi đó: $\vec{P M} = \vec{A N}$ (2).

Từ (1) và (2) suy ra: $\vec{P B} + \vec{M C} = \vec{A N}$

Hoạt động 3 trang 84 Toán lớp 10: Cho ABCD là hình bình hành (Hình 52). So sánh:

a) Hai vectơ $\vec{A D}$ và $\vec{B C}$ .

b) Vectơ tổng $\vec{A B} + \vec{A D}$ và vectơ $\vec{A C}$ .

Cho ABCD là hình bình hành (Hình 52). So sánh: Hai vectơ AD và BC

Lời giải:

a) Ta có ABCD là hình bình hành nên AD // BC và AD = BC.

Suy ra: $\vec{A D}$ = $\vec{B C}$ .

Vậy $\vec{A D}$ = $\vec{B C}$ .

b) Ta có: $\vec{A B} + \vec{A D} = \vec{A B} + \vec{B C} = \vec{A C}$

Vậy $\vec{A B} + \vec{A D} = \vec{A C}$

Luyện tập 2 trang 84 Toán lớp 10: Hãy giải thích hướng đi của thuyền ở Hình 48.

Lời giải:

Hãy giải thích hướng đi của thuyền ở Hình 48

Theo quy tắc hình bình hành, ta có $\vec{F} = \vec{F_{1}} + \vec{F_{2}}$ .

Trên Hình 48 ta có: hai người đi dọc hai bên bờ sông và cùng kéo một con thuyền với hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ . Hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ tạo nên hợp lực $\vec{F}$ là tổng của hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ , làm thuyền chuyển động theo hướng của vectơ $\vec{F}$ .

Giải Toán 10 trang 85 Tập 1

Luyện tập 3 trang 85 Toán lớp 10: Cho hình bình hành ABCD và điểm E bất kì. Chứng minh $\vec{A B} + \vec{C E} + \vec{A D} = \vec{A E}$ .

Lời giải:

Cho hình bình hành ABCD và điểm E bất kì. Chứng minh vectơ AB +vectơ CE + vectơ AD = vectơ AE

Do ABCD là hình bình hành nên $\vec{A B} + \vec{A D} = \vec{A C}$ (1).

Khi đó với E là điểm bất kì ta có:

$\vec{A B} + \vec{C E} + \vec{A D} = (\vec{A B} + \vec{A D}) + \vec{C E}$ (2) (tính chất giao hoán và kết hợp)

Từ (1) và (2) suy ra: $\vec{A B} + \vec{C E} + \vec{A D} = \vec{A C} + \vec{C E} = \vec{A E}$

Vậy $\vec{A B} + \vec{C E} + \vec{A D} = \vec{A E}$

2. Hiệu của hai vectơ

Hoạt động 4 trang 85 Toán lớp 10: Trong Hình 54, hai ròng rọc có trục quay nằm ngang và song song với nhau, hai vật có trọng lượng bằng nhau. Mỗi dây có một đầu buộc vào vật, một đầu buộc vào một mảnh nhựa cứng. Hai vật lần lượt tác động lên mảnh nhựa các lực $\vec{F_{1}}, \vec{F_{2}}$ . Nhận xét về hướng và độ dài của mỗi cặp vectơ sau:

a) $\vec{P_{1}}$ và $\vec{P_{2}}$ biểu diễn trọng lực của hai vật;

b) $\vec{F_{1}}$ và $\vec{F_{2}}$ .

(Bỏ qua trọng lượng của các dây và các lực ma sát)

Trong Hình 54, hai ròng rọc có trục quay nằm ngang và song song với nhau, hai vật có trọng lượng

Lời giải:

a) Quan sát Hình 54 ta thấy, hai vectơ $\vec{P_{1}}$ và $\vec{P_{2}}$ có cùng hướng và độ dài.

b) Hai vectơ $\vec{F_{1}}$ và $\vec{F_{2}}$ ngược hướng và cùng độ dài.

Giải Toán 10 trang 86 Tập 1

Hoạt động 5 trang 86 Toán lớp 10: Cho hai vectơ $\vec{a}, \vec{b}$ . Lấy một điểm M tùy ý.

a) Vẽ $\vec{M A} = \vec{a}, \vec{M B} = \vec{b}, \vec{M C} = - \vec{b}$ (Hình 56).

b) Tổng của hai vectơ $\vec{a}$ và $(- \vec{b})$ bằng vectơ nào?

Lời giải:

a) Lấy điểm M tùy ý, qua M vẽ đường thẳng song song với giá của vectơ $\vec{a}$ , trên đường thẳng này về phía cùng hướng với vectơ $\vec{a}$ , lấy điểm A sao cho $|\vec{M A}| = |\vec{a}|$ .

Qua M, tiếp tục vẽ đường thẳng song song với giá của vectơ $\vec{b}$ , trên đường thẳng này về phía cùng hướng với vectơ $\vec{b}$ , lấy điểm B sao cho $|\vec{M B}| = |\vec{b}|$ , về phía ngược hướng với vectơ $\vec{b}$ , lấy điểm C sao cho $|\vec{M C}| = |\vec{b}|$ .

Vậy ta vẽ được các vectơ $\vec{M A} = \vec{a}, \vec{M B} = \vec{b}, \vec{M C} = - \vec{b}$ như hình vẽ.

Cho hai vectơ a, b . Lấy một điểm M tùy ý

b) Tổng của hai vectơ $\vec{a}$ và $(- \vec{b})$ bằng vectơ $\vec{M N}$ với N là đỉnh thứ tư của hình bình hành AMCN.

Luyện tập 4 trang 86 Toán lớp 10: Cho tam giác ABC có M là trung điểm của AC, N là trung điểm của BC và AB = a. Tính độ dài vectơ $\vec{C M} - \vec{N B}$ .

Lời giải:

Cho tam giác ABC có M là trung điểm của AC, N là trung điểm của BC và AB = a

Vì N là trung điểm của BC nên $\vec{N B} = \vec{C N}$ .

Nên ta có:

$\vec{C M} - \vec{N B} = \vec{C M} - \vec{C N} = \vec{C M} + (- \vec{C N}) = \vec{C M} + \vec{N C} = \vec{N C} + \vec{C M} = \vec{N M}$

Do M và N lần lượt là trung điểm của AC và BC nên MN là đường trung bình của tam giác ABC nên MN = $\frac{1}{2}$ AB = $\frac{1}{2} a$ .

Khi đó: $|\vec{M N}| = M N = \frac{1}{2} a$

Vậy $|\vec{C M} - \vec{N B}| = |M N| = \frac{1}{2} a .$

Bài tập

Giải Toán 10 trang 87 Tập 1

Bài 1 trang 87 Toán lớp 10: Cho ba điểm M, N, P. Vectơ $\vec{u} = \vec{N P} + \vec{M N}$ bằng vectơ nào sau đây?

A. $\vec{P N}$ ;

B. $\vec{P M}$ ;

C. $\vec{M P}$ ;

D. $\vec{N M}$ .

Lời giải:

Đáp án đúng là: C.

Với ba điểm M, N, P bất kì ta có: $\vec{u} = \vec{N P} + \vec{M N} = \vec{M N} + \vec{N P} = \vec{M P}$ .

Bài 2 trang 87 Toán lớp 10: Cho ba điểm D, E, G. Vectơ $\vec{v} = \vec{D E} + (- \vec{D G})$ bằng vectơ nào sau đây?

A. $\vec{E G}$ ;

B. $\vec{G E}$ ;

C. $\vec{G D}$ ;

D. $\vec{E D}$ .

Lời giải:

Đáp án đúng là: B.

Với ba điểm D, E, G bất kì ta có:

$\vec{v} = \vec{D E} + (- \vec{D G}) = \vec{D E} + \vec{G D} = \vec{G D} + \vec{D E} = \vec{G E}$ .

Bài 3 trang 87 Toán lớp 10: Cho bốn điểm A, B, C, D. Chứng minh:

a) $\vec{A B} + \vec{C D} = \vec{A D} + \vec{C B}$ ;

b) $\vec{A B} + \vec{C D} + \vec{B C} + \vec{D A} = \vec{0}$ .

Lời giải:

a) Với bốn điểm A, B, C, D bất kì ta có:

$\vec{A B} = \vec{A D} + \vec{D B}$

Nên:

$\vec{A B} + \vec{C D} = (\vec{A D} + \vec{D B}) + \vec{C D} = \vec{A D} + (\vec{C D} + \vec{D B})$

$= \vec{A D} + \vec{C B}$

Vậy $\vec{A B} + \vec{C D} = \vec{A D} + \vec{C B}$ .

b) Ta có:

$\vec{A B} + \vec{C D} + \vec{B C} + \vec{D A}$

$= (\vec{A B} + \vec{B C}) + (\vec{C D} + \vec{D A})$ (tính chất giao hoán và kết hợp)

$= \vec{A C} + \vec{C A}$

$= \vec{0}$ .

Vậy $\vec{A B} + \vec{C D} + \vec{B C} + \vec{D A} = \vec{0}$ .

Bài 4 trang 87 Toán lớp 10: Cho hình bình hành ABCD, gọi O là giao điểm của AC và BD. Các khẳng định sau đúng hay sai?

a) $|\vec{A B} + \vec{A D}| = |\vec{A C}|$ ;

b) $\vec{A B} + \vec{B D} = \vec{C B}$ ;

c) $\vec{O A} + \vec{O B} = \vec{O C} + \vec{O D}$ .

Lời giải:

Cho hình bình hành ABCD, gọi O là giao điểm của AC và BD. Các khẳng định

+ Do ABCD là hình bình hành nên $\vec{A B} + \vec{A D} = \vec{A C}$ .

Do đó: $|\vec{A B} + \vec{A D}| = |\vec{A C}|$ . Vậy khẳng định a) đúng.

+ Ta có: $\vec{A B} + \vec{B D} = \vec{A D}$

Mà $\vec{A D} = \vec{B C}$ (do ABCD là hình bình hành)

Do đó: $\vec{A B} + \vec{B D} = \vec{A D} = \vec{B C} = - \vec{C B}$ .

Vậy khẳng định b) sai.

+ Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên O là trung điểm của AC và BD.

Khi đó ta có: $\vec{O A} = \vec{C O}; \vec{O D} = \vec{B O}$

Do đó: $\{\begin{cases} \vec{O A} + \vec{O B} = \vec{C O} + \vec{O B} = \vec{C B} = - \vec{B C} \\ \vec{O C} + \vec{O D} = \vec{O C} + \vec{B O} = \vec{B O} + \vec{O C} = \vec{B C} \end{cases}$

Suy ra: $\vec{O A} + \vec{O B} = - (\vec{O C} + \vec{O D})$ .

Vậy khẳng định c) sai.

Bài 5 trang 87 Toán lớp 10: Cho đường tròn tâm O. Giả sử A, B là hai điểm nằm trên đường tròn. Tìm điều kiện cần và đủ để hai vectơ $\vec{O A}$ và $\vec{O B}$ đối nhau.

Lời giải:

Hai vectơ $\vec{O A}$ và $\vec{O B}$ đối nhau khi chúng cùng độ dài và ngược hướng.

Ta có A, B nằm trên đường tròn tâm O nên OA, OB là bán kính, do đó: OA = OB.

Khi đó: $|\vec{O A}| = |\vec{O B}|$

Ta cần thêm điều kiện hai vectơ $\vec{O A}$ và $\vec{O B}$ ngược hướng, tức là chúng cùng phương và ngược chiều, do đó giá của $\vec{O A}$ chính là đường thẳng OA và giá của vectơ $\vec{O B}$ chính là đường thẳng OB phải song song hoặc trùng nhau.

OA và OB giao nhau tại O nên không xảy ra trường hợp song song.

Vậy đường thẳng OA trùng với đường thẳng OB, hay O, B, A thẳng hàng, hay AB là đường kính của đường tròn (O).

Cho đường tròn tâm O. Giả sử A, B là hai điểm nằm trên đường tròn. Tìm điều kiện

Vậy điều kiện cần và đủ để hai vectơ $\vec{O A}$ và $\vec{O B}$ đối nhau là AB là đường kính của đường tròn (O).

Bài 6 trang 87 Toán lớp 10: Cho ABCD là hình bình hành. Chứng minh $\vec{M B} - \vec{M A} = \vec{M C} - \vec{M D}$ với mọi điểm M trong mặt phẳng.

Lời giải:

Cho ABCD là hình bình hành. Chứng minh vectơ MB - vectơ MA = vectơ MC -vectơ MD với mọi điểm M trong mặt phẳng

Ta có:

$\vec{M B} - \vec{M A} = \vec{M B} + (- \vec{M A}) = \vec{M B} + \vec{A M} = \vec{A M} + \vec{M B} = \vec{A B}$ (1).

$\vec{M C} - \vec{M D} = \vec{M C} + (- \vec{M D}) = \vec{M C} + \vec{D M} = \vec{D M} + \vec{M C} = \vec{D C}$ (2).

Do ABCD là hình bình hành nên AB // DC và AB = DC, do đó: $\vec{A B} = \vec{D C}$ (3).

Từ (1), (2) và (3) suy ra: $\vec{M B} - \vec{M A} = \vec{M C} - \vec{M D}$ .

Bài 7 trang 87 Toán lớp 10: Cho hình vuông ABCD có cạnh a. Tính độ dài của các vectơ sau:

a) $\vec{D A} + \vec{D C}$ ;

b) $\vec{A B} - \vec{A D}$ ;

c) $\vec{O A} + \vec{O B}$ với O là giao điểm của AC và BD.

Lời giải:

Cho hình vuông ABCD có cạnh a. Tính độ dài của các vectơ sau

a) Tam giác ABD vuông tại A (hình vuông ABCD), áp dụng định lí Pythagore, ta có: BD2 = AD2 + AB2 = a2 + a2 = 2a2

$\Rightarrow B D = a \sqrt{2}$ .

Vì ABCD là hình vuông nên DA // CB và DA = CB, do đó: $\vec{D A} = \vec{C B}$

Khi đó:

$\vec{D A} + \vec{D C} = \vec{C B} + \vec{D C} = \vec{D C} + \vec{C B} = \vec{D B}$

Suy ra: $|\vec{D A} + \vec{D C}| = |\vec{D B}| = D B = a \sqrt{2}$ .

Vậy $|\vec{D A} + \vec{D C}| = a \sqrt{2}$ .

b) Ta có:

$\vec{A B} - \vec{A D} = \vec{A B} + (- \vec{A D}) = \vec{A B} + \vec{D A} = \vec{D A} + \vec{A B} = \vec{D B}$

Do đó: $|\vec{A B} - \vec{A D}| = |\vec{D B}| = D B = a \sqrt{2}$ .

Vậy $|\vec{A B} - \vec{A D}| = a \sqrt{2}$ .

c) O là giao điểm hai đường chéo của hình vuông ABCD nên O là trung điểm của AC và BD.

Do đó ta có: $\vec{O A} = \vec{C O}$

Khi đó: $\vec{O A} + \vec{O B} = \vec{C O} + \vec{O B} = \vec{C B}$ .

Suy ra $|\vec{O A} + \vec{O B}| = \vec{|C B|} = C B = a$ .

Vậy $|\vec{O A} + \vec{O B}| = a$ .

Bài 8 trang 87 Toán lớp 10: Cho ba lực $\vec{F_{1}} = \vec{O A}, \vec{F_{2}} = \vec{O B}$ và $\vec{F_{3}} = \vec{O C}$ cùng tác động vào một vật tại điểm O và vật đứng yên. Cho biết cường độ của $\vec{F_{1}}, \vec{F_{2}}$ đều là 120 N và $\hat{A O B} = 120 °$ . Tìm cường độ và hướng của lực $\vec{F_{3}}$ .

Lời giải:

Cho ba lực vectơ F1 = vectơ OA, vectơ F2 = vectơ OB và vectơ F3= vectơ OC cùng tác động vào một vật tại điểm O

Vì ba lực $\vec{F_{1}}, \vec{F_{2}}, \vec{F_{3}}$ cùng tác động vào vật tại điểm O và vật đứng yên.

Do đó: $\vec{F_{1}} + \vec{F_{2}} + \vec{F_{3}} = \vec{0}$ $\Leftrightarrow \vec{F_{3}} = - (\vec{F_{1}} + \vec{F_{2}})$ (1).

Ta cần tính $\vec{F_{1}} + \vec{F_{2}}$ .

Cường độ của $\vec{F_{1}}$ và $\vec{F_{2}}$ đều là 120 N.

$\Rightarrow |\vec{F_{1}}| = |\vec{F_{2}}| = 120 N .$

Dựng hình bình hành OADB có $\vec{F_{1}} = \vec{O A}, \vec{F_{2}} = \vec{O B}$ và $\hat{A O B} = 120 °$ .

Do đó OA = OB = 120 nên OADB là hình thoi.

Gọi E là giao điểm của hai đường chéo AB và OD thì E là trung điểm của mỗi đường.

Đường chéo OD đồng thời là tia phân giác của góc AOB.

Suy ra: $\hat{A O D} = \frac{1}{2} \hat{A O B} = \frac{1}{2} .120 ° = 60 °$ .

Xét tam giác OAD có: OA = AD (tính chất hình thoi OADB)

Suy ra tam giác OAD cân tại A.

Mà $\hat{A O D} = 60 °$ .

Do đó tam giác AOD là tam giác đều.

Suy ra: OD = OA = 120.

Do OADB là hình bình hành nên $\vec{O D} = \vec{O A} + \vec{O B}$ .

$\Rightarrow \vec{O D} = \vec{F_{1}} + \vec{F_{2}}$ (2).
Từ (1) và (2) suy ra: $\vec{F_{3}} = - (\vec{F_{1}} + \vec{F_{2}}) = - \vec{O D}$ .

Vậy lực $\vec{F_{3}}$ có hướng ngược với hướng của $\vec{O D}$ và có cường độ: $|\vec{F_{3}}| = |\vec{O D}| = 120 N .$

Bài 9 trang 87 Toán lớp 10: Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc là 10 km/h. Một chiếc ca nô chuyển động từ phía đông sang phía tây với vận tốc 40 km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông.

Lời giải:

Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc là 10 km/h. Một chiếc ca nô

Ca nô chuyển từ đông sang tây, giả sử ca nô đi theo hướng A sang C, khi đó vận tốc so với mặt nước của ca nô được biểu thị bởi $\vec{v_{1}} = \vec{A C}$ và có độ lớn $|\vec{v_{1}}| = 40 k m / h$ , vận tốc dòng chảy được biểu thị bởi $\vec{v_{2}} = \vec{A B}$ và có độ lớn $|\vec{v_{2}}| = 10 k m / h$ .

Khi đó vận tốc của ca nô so với bờ sông được biểu thị bởi $\vec{v} = \vec{v_{1}} + \vec{v_{2}}$

Ta cần tính độ lớn của vectơ $\vec{v}$ , hay chính là $|\vec{v_{1}} + \vec{v_{2}}|$

Dựng hình bình hành ACDB như hình vẽ.

Do hướng nam bắc vuông góc với hướng đông tây nên AB và AC vuông góc với nhau.

Suy ra ACDB là hình chữ nhật.

Nên AB = CD = 10, AC = BD = 40.

Sử dụng định lí Pythagore trong tam giác vuông ACD, ta có:

AD2 = AC2 + CD2 = 402 + 102 = 1700

$\Rightarrow A D = \sqrt{1700} = 10 \sqrt{17}$

Lại có do ACDB là hình bình hành nên: $\vec{A D} = \vec{A C} + \vec{A B} = \vec{v_{1}} + \vec{v_{2}}$

Do đó: $\vec{v} = \vec{A D} \Rightarrow |\vec{v}| = |\vec{A D}| = A D = 10 \sqrt{17}$ .

Vậy vận tốc của ca nô so với bờ sông là $10 \sqrt{17}$ km/h.

Lý thuyết Tổng và hiệu của hai vectơ

1. Tổng của hai vectơ

1.1. Định nghĩa

– Với ba điểm bất kì A, B, C, vectơ $\vec{AC}$ được gọi là tổng của hai vectơ $\vec{AB}$ và $\vec{BC}$ , kí hiệu là $\vec{AC}$ = $\vec{AB}$ + $\vec{BC}$ .

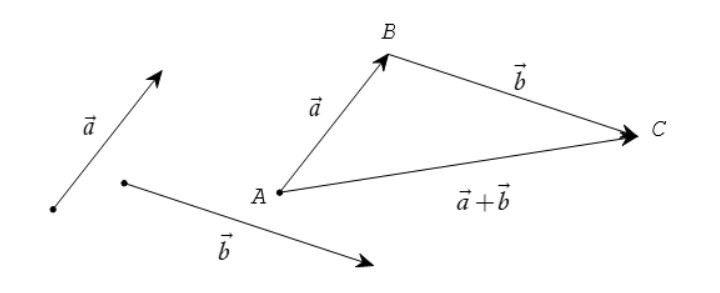
Tổng và hiệu của hai vectơ (Lý thuyết + Bài tập Toán lớp 10) – Cánh diều (ảnh 1)

– Cho hai vectơ $\vec{a}$ và $\vec{b}$ . Lấy một điểm A tùy ý, vẽ $\vec{AB}$ = $\vec{a}$ và $\vec{BC}$ = $\vec{b}$ . Vectơ $\vec{AB}$ được gọi là tổng của hai vectơ $\vec{a}$ và $\vec{b}$ . Ta kí hiệu tổng của hai vectơ $\vec{a}$ và $\vec{b}$ là $\vec{a}$ + $\vec{b}$ . Vậy $\vec{AC}$ = $\vec{a}$ + $\vec{b}$ .

Phép lấy tổng của hai vectơ còn được gọi là phép cộng vectơ.

Ví dụ: Cho hình chữ nhật ABCD tâm O. Tính:

a) $\vec{OA}$ + $\vec{DC}$

b) $\vec{BC}$ + $\vec{OA}$

Hướng dẫn giải:

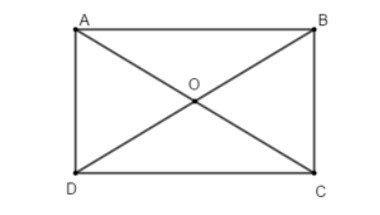
Tổng và hiệu của hai vectơ (Lý thuyết + Bài tập Toán lớp 10) – Cánh diều (ảnh 1)

a) Vì ABCD là hình chữ nhật nên AB // CD và AB = CD.

⇒ $\vec{DC}$ = $\vec{AB}$ .

⇒ $\vec{OA}$ + $\vec{DC}$ = $\vec{OA}$ + $\vec{AB}$ = $\vec{OB}$ .

b) Vì A, O, C thẳng hàng (O là trung điểm của đường chéo AC)

⇒ $\vec{OA}$ = $\vec{CO}$ .

⇒ $\vec{BC}$ + $\vec{OA}$ = $\vec{BC}$ + $\vec{CO}$ = $\vec{BO}$ .

1.2. Quy tắc hình bình hành

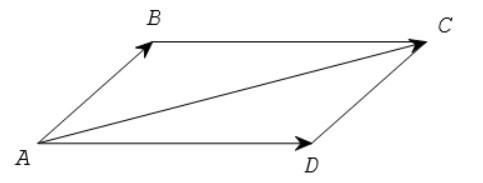
Tổng và hiệu của hai vectơ (Lý thuyết + Bài tập Toán lớp 10) – Cánh diều (ảnh 1)

Nếu ABCD là hình bình hành thì $\vec{AB}$ + $\vec{AD}$ = $\vec{AC}$ .

Ví dụ: Chứng minh quy tắc hình bình hành.

Hướng dẫn giải:

Ta có: $\vec{AD}$ = $\vec{BC}$ .

Suy ra: $\vec{AB}$ + $\vec{AD}$ = $\vec{AB}$ + $\vec{BC}$ = $\vec{AC}$ .

1.3. Tính chất

Với ba vectơ tùy ý $\vec{a}$ , $\vec{b}$ , $\vec{c}$ ta có:

$\vec{a}$ + $\vec{b}$ = $\vec{b}$ + $\vec{a}$ (tính chất giao hoán) ;

( $\vec{a}$ + $\vec{b}$ ) + $\vec{c}$ = $\vec{a}$ + ( $\vec{b}$ + $\vec{c}$ ) (tính chất kết hợp);

$\vec{a}$ + $\vec{0}$ = $\vec{0}$ + $\vec{a}$ = $\vec{a}$ (tính chất của vectơ–không).

Chú ý: Tổng ba vectơ $\vec{a}$ + $\vec{b}$ + $\vec{c}$ được xác định theo một trong hai cách sau:

( $\vec{a}$ + $\vec{b}$ ) + $\vec{c}$ hoặc $\vec{a}$ + ( $\vec{b}$ + $\vec{c}$ ).

Ví dụ: Cho 5 điểm tùy ý A, B, C, D, E. Chứng minh rằng:

a) $\vec{CD} + \vec{EC} + \vec{DA} + \vec{BE}$ = $\vec{BA}$ .

b) $\vec{AB}$ + $\vec{CD}$ + $\vec{EA}$ = $\vec{CB}$ + $\vec{ED}$ .

Hướng dẫn giải:

a) Ta có:

$\vec{CD} + \vec{EC} + \vec{DA} + \vec{BE}$

= $\vec{CD} + \vec{DA} + \vec{BE} + \vec{EC}$ (áp dụng tính chất giao hoán)

= $(\vec{CD} + \vec{DA}) + (\vec{BE} + \vec{EC})$ (áp dụng tính chất kết hợp)

= $\vec{CA} + \vec{BC}$ (áp dụng quy tắc cộng vectơ)

= $\vec{BC} + \vec{CA}$ (áp dụng tính chất giao hoán)

= $\vec{BA}$ (áp dụng quy tắc cộng vectơ) (đpcm).

Vậy $\vec{CD} + \vec{EC} + \vec{DA} + \vec{BE}$ = $\vec{BA}$ .

b) Ta có:

$\vec{AB}$ + $\vec{CD}$ + $\vec{EA}$

= $(\vec{AC} + \vec{CB}) + \vec{CD} + (\vec{ED} + \vec{DA})$ (áp dụng quy tắc cộng vectơ)

= $\vec{CB} + \vec{ED} + \vec{AC} + \vec{CD} + \vec{DA}$ (áp dụng tính chất giao hoán)

= $\vec{CB} + \vec{ED} + (\vec{AC} + \vec{CD}) + \vec{DA}$ (áp dụng tính chất kết hợp)

= $\vec{CB} + \vec{ED} + \overset{⇀}{AD} + \vec{DA}$ (áp dụng quy tắc cộng vectơ)

= $\vec{CB} + \vec{ED} + (\overset{⇀}{AD} + \vec{DA})$ (áp dụng tính chất kết hợp)

= $\vec{CB} + \vec{ED} + \vec{AA}$

= $\vec{CB} + \vec{ED} + \vec{0}$ (vectơ có điểm đầu và điểm cuối trùng nhau là vectơ–không)

= $\vec{CB} + \vec{ED}$ (áp dụng tính chất vectơ–không) (đpcm).

2. Hiệu của hai vectơ

2.1. Hai vectơ đối nhau

Định nghĩa: Vectơ có cùng độ dài và ngược hướng với vectơ $\vec{a}$ được gọi là vectơ đối của vectơ $\vec{a}$ , kí hiệu là – $\vec{a}$ . Hai vectơ $\vec{a}$ và – $\vec{a}$ được gọi là hai vectơ đối nhau.

Quy ước: Vectơ đối của vectơ $\vec{0}$ là vectơ $\vec{0}$ .

Nhận xét:

+) $\vec{a}$ + (– $\vec{a}$ ) = (– $\vec{a}$ ) + $\vec{a}$ = $\vec{0}$

+) Hai vectơ $\vec{a}$ , $\vec{b}$ là hai vectơ đối nhau khi và chỉ khi $\vec{a}$ + $\vec{b}$ = $\vec{0}$ .

+) Với hai điểm A, B, ta có: $\vec{AB} + \vec{BA} = \vec{0}$ .

Lưu ý: Cho hai điểm A, B. Khi đó hai vectơ $\vec{AB}$ và $\vec{BA}$ là hai vectơ đối nhau, tức là $\vec{BA} = - \vec{AB} .$

Chú ý:

– I là trung điểm của đoạn thẳng AB khi và chỉ khi $\vec{IA} + \vec{IB} = \vec{0}$ .

– G là trọng tâm của tam giác ABC khi và chỉ khi $\vec{GA} + \vec{GB} + \vec{GC} = \vec{0}$ .

Ví dụ: Cho hình vuông ABCD có tâm O. Tìm vectơ đối của các vectơ $\vec{AB}$ , $\vec{AO}$ .

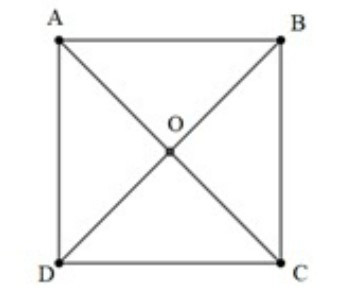
Tổng và hiệu của hai vectơ (Lý thuyết + Bài tập Toán lớp 10) – Cánh diều (ảnh 1)

Hướng dẫn giải:

+ Vì $|\vec{BA}| = |\vec{AB}|$ = AB và $\vec{BA}$ ngược hướng với $\vec{AB}$

⇒ $\vec{BA}$ = – $\vec{AB}$

Þ $\vec{BA}$ là vectơ đối của vectơ $\vec{AB}$ .

+ Vì AB = CD, AB // CD (ABCD là hình vuông)

⇒ $|\vec{AB}| = |\vec{CD}|$ và $\vec{CD}$ ngược hướng với $\vec{AB}$

⇒ $\vec{CD}$ = – $\vec{AB}$

Þ $\vec{CD}$ là vectơ đối của vectơ $\vec{AB}$ .

Vì A, O, C là ba điểm thẳng hàng và OA = OC (ABCD là hình vuông)

⇒ $\vec{AO}$ ngược hướng với $\vec{CO}$ và $|\vec{AO}| = |\vec{CO}|$

⇒ $\vec{CO}$ = – $\vec{AO}$

Þ $\vec{CO}$ là vectơ đối của $\vec{AO}$ .

Vậy $\vec{BA}$ , $\vec{CD}$ là vectơ đối của vectơ $\vec{AB}$ và $\vec{CO}$ là vectơ đối của $\vec{AO}$ .

2.2. Hiệu của hai vectơ

Hiệu của hai vectơ $\vec{a}$ và $\vec{b}$ , kí hiệu là $\vec{a}$ – $\vec{b}$ , là tổng của vectơ $\vec{a}$ và vectơ đối của vectơ $\vec{b}$ , tức là $\vec{a}$ – $\vec{b}$ = $\vec{a}$ + (– $\vec{b}$ ).