Với giải Bài 6 trang 87 SGK Toán lớp 10 Cánh diều chi tiết trong Bài 4: Tổng và hiệu của hai vectơ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SGK Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 4: Tổng và hiệu của hai vectơ
Bài 6 trang 87 Toán lớp 10: Cho ABCD là hình bình hành. Chứng minh với mọi điểm M trong mặt phẳng.
Lời giải:
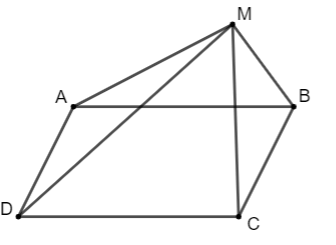
Ta có:
(1).
(2).
Do ABCD là hình bình hành nên AB // DC và AB = DC, do đó: (3).
Từ (1), (2) và (3) suy ra: .
Bài tập vận dụng:
Bài 1. Cho hình vuông ABCD tâm O. Tính tổng và .
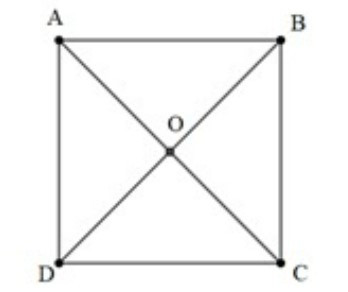
Hướng dẫn giải:
+ Vì ABCD là hình vuông nên AB // DC và AB = DC.
⇒
⇒
Áp dụng quy tắc cộng hai vectơ ta có:
Do đó, = .
+ Vì A, O, C cùng nằm trên một đường thẳng và OA = OC (O là tâm hình vuông ABCD).
⇒
⇒
Áp dụng quy tắc công hai vectơ ta có:
Vậy = .
Bài 2. Cho tam giác ABC có G là trọng tâm của tam giác.
Tính độ dài vectơ .
Hướng dẫn giải:
Vì G là trọng tâm tam giác ABC nên ta áp dụng quy tắc trọng tâm có:
⇒
Vậy độ dài vectơ là 0.
Câu 1. Cho ba điểm phân biệt A, B, C. Đẳng thức nào sau đây đúng?
A.
B.
C.
D.
Hướng dẫn giải
Đáp án đúng là: C
Xét các đáp án:
- Đáp án A. Ta có . Vậy A sai.
- Đáp án B sai vì .
- Đáp án C. Ta có . Vậy C đúng.
Xem thêm lời giải bài tập SGK Toán 10 Cánh diều hay, chi tiết khác:
Câu hỏi khởi động trang 83 Toán lớp 10: Quan sát hình ảnh hai người cùng kéo một chiếc thuyền theo hai hướng khác nhau (Hình 48). Tuy nhiên, chiếc thuyền lại không di chuyển theo cùng hướng với một trong hai người đó mà di chuyển theo hướng khác......
Hoạt động 1 trang 83 Toán lớp 10: Một vật dịch chuyển từ A đến B và tiếp tục dịch chuyển từ B đến C (Hình 49)....
Hoạt động 2 trang 83 Toán lớp 10: Cho hai vectơ . Lấy một điểm A tùy ý......
Luyện tập 1 trang 84 Toán lớp 10: Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh .....
Hoạt động 3 trang 84 Toán lớp 10: Cho ABCD là hình bình hành (Hình 52). So sánh:.....
Luyện tập 2 trang 84 Toán lớp 10: Hãy giải thích hướng đi của thuyền ở Hình 48......
Luyện tập 3 trang 85 Toán lớp 10: Cho hình bình hành ABCD và điểm E bất kì. Chứng minh ....
Hoạt động 4 trang 85 Toán lớp 10: Trong Hình 54, hai ròng rọc có trục quay nằm ngang và song song với nhau, hai vật có trọng lượng bằng nhau. Mỗi dây có một đầu buộc vào vật, một đầu buộc vào một mảnh nhựa cứng. Hai vật lần lượt tác động lên mảnh nhựa các lực . Nhận xét về hướng và độ dài của mỗi cặp vectơ sau:.....
Hoạt động 5 trang 86 Toán lớp 10: Cho hai vectơ . Lấy một điểm M tùy ý......
Luyện tập 4 trang 86 Toán lớp 10: Cho tam giác ABC có M là trung điểm của AC, N là trung điểm của BC và AB = a. Tính độ dài vectơ .......
Bài 1 trang 87 Toán lớp 10: Cho ba điểm M, N, P. Vectơ bằng vectơ nào sau đây?.....
Bài 2 trang 87 Toán lớp 10: Cho ba điểm D, E, G. Vectơ bằng vectơ nào sau đây?.....
Bài 3 trang 87 Toán lớp 10: Cho bốn điểm A, B, C, D. Chứng minh:.....
Bài 4 trang 87 Toán lớp 10: Cho hình bình hành ABCD, gọi O là giao điểm của AC và BD. Các khẳng định sau đúng hay sai?.....
Bài 5 trang 87 Toán lớp 10: Cho đường tròn tâm O. Giả sử A, B là hai điểm nằm trên đường tròn. Tìm điều kiện cần và đủ để hai vectơ và đối nhau......
Bài 6 trang 87 Toán lớp 10: Cho ABCD là hình bình hành. Chứng minh với mọi điểm M trong mặt phẳng......
Bài 7 trang 87 Toán lớp 10: Cho hình vuông ABCD có cạnh a. Tính độ dài của các vectơ sau:.....
Bài 8 trang 87 Toán lớp 10: Cho ba lực và cùng tác động vào một vật tại điểm O và vật đứng yên. Cho biết cường độ của đều là 120 N và . Tìm cường độ và hướng của lực ......
Bài 9 trang 87 Toán lớp 10: Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc là 10 km/h. Một chiếc ca nô chuyển động từ phía đông sang phía tây với vận tốc 40 km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông......
Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:
Bài 3: Khái niệm vectơ
Bài 4: Tổng và hiệu của hai vectơ
Bài 5: Tích của một số với một vectơ
Bài 6: Tích vô hướng của hai vectơ
Giải SGK Toán 10 Bài tập cuối chương 4
