Giải SGK Toán 10 Bài 6 (Cánh diều): Tích vô hướng của hai vectơ

Nguyễn Thị Thuỳ Linh Ngày: 24-08-2024 Lớp 10

3.1 K

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 6: Tích vô hướng của hai vectơ chi tiết sách Toán 10 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 6: Tích vô hướng của hai vectơ

Giải Toán 10 trang 93 Tập 1

Câu hỏi khởi động trang 93 Toán lớp 10: Trong vật lí, nếu có một lực $\vec{F}$ tác động lên một vật tại điểm O và làm cho vật đó di chuyển một quãng đường s = OM (Hình 63) thì công A của lực $\vec{F}$ được tính theo công thức $A = |\vec{F}| . |\vec{O M}| . \cos φ$ trong đó $|\vec{F}|$ gọi là cường độ của lực $\vec{F}$ tính bằng Newton (N), $|\vec{O M}|$ là độ dài của vectơ $\vec{O M}$ tính bằng mét (m), φ là góc giữa hai vectơ $\vec{O M}$ và $\vec{F}$ , còn công A tính bằng Jun (J).

Trong vật lí, nếu có một lực vectơ F tác động lên một vật tại điểm O

Trong toán học, giá trị của biểu thức $A = |\vec{F}| . |\vec{O M}| . \cos φ$ (không kể đơn vị đo) được gọi là gì?

Lời giải:

Giá trị của biểu thức $A = |\vec{F}| . |\vec{O M}| . \cos φ$ là tích vô hướng của hai vectơ $\vec{F}$ và $\vec{O M}$ .

1. Định nghĩa

Luyện tập 1 trang 93 Toán lớp 10: Cho tam giác ABC vuông tại A có $\hat{B} = 30 °$ , AB = 3 cm. Tính $\vec{B A} . \vec{B C}; \vec{C A} . \vec{C B}$ .

Lời giải:

Cho tam giác ABC vuông tại A có góc B = 30 độ, AB = 3 cm. Tính vectơ BA.vectơ BC; vectơ CA. vectơ CB

Ta có tam giác ABC vuông ở A nên $\hat{B} + \hat{C} = 90 °$

$\Rightarrow \hat{C} = 90 ° - \hat{B} = 90 ° - 30 ° = 60 °$ .

Lại có: tan B = $\frac{A C}{A B}$ ⇒ AC = AB . tan0B = 3 . tan 30° = $\sqrt{3}$ .

Và sin B = $\frac{A C}{B C}$ ⇒ BC = $\frac{A C}{\sin B} = \frac{\sqrt{3}}{\sin 30 °} = 2 \sqrt{3}$ .

Ta có: $\vec{B A} . \vec{B C} =$ $|\vec{B A}| . |\vec{B C}| . \cos (\vec{B A}, \vec{B C})$ = $3 . 2 \sqrt{3} . \cos \hat{A B C}$ = $6 \sqrt{3} . \cos 30 ° = 9$ .

$\vec{C A} . \vec{C B}$ = $|\vec{C A}| . |\vec{C B}| . \cos (\vec{C A}, \vec{C B})$ = $\sqrt{3} . 2 \sqrt{3} . \cos \hat{A C B}$ = 6 . cos 60° = 3.

Vậy $\vec{B A} . \vec{B C} = 9$ và $\vec{C A} . \vec{C B} = 3$ .

Giải Toán 10 trang 95 Tập 1

Luyện tập 2 trang 95 Toán lớp 10: Cho tam giác ABC đều cạnh a, AH là đường cao. Tính:

a) $\vec{C B} . \vec{B A}$ ;

b) $\vec{A H} . \vec{B C}$ .

Lời giải:

Cho tam giác ABC đều cạnh a, AH là đường cao. Tính

a) Tam giác ABC đều nên $\hat{A} = \hat{B} = \hat{C} = 60 °$ và AB = BC = AC = a.

Lại có: $(\vec{B C}, \vec{B A}) = \hat{A B C} = 60 °$ .

Ta có:

$\vec{C B} . \vec{B A} = (- \vec{B C}) . \vec{B A}$

$= - (\vec{B C} . \vec{B A})$

$= - (|\vec{B C}| . |\vec{B A}| . \cos (\vec{B C}, \vec{B A}))$

$= - (a . a . \cos 60 °) = \frac{- a^{2}}{2}$

Vậy $\vec{C B} . \vec{B A} = \frac{- a^{2}}{2}$ .

b) Do AH là đường cao của tam giác ABC nên AH ⊥ BC.

Do đó: $\vec{A H} ⊥ \vec{B C}$ nên $\vec{A H} . \vec{B C} = 0$ .

2. Tính chất

Giải Toán 10 trang 96 Tập 1

Luyện tập 3 trang 96 Toán lớp 10: Chứng minh rằng với hai vectơ bất kì $\vec{a}, \vec{b}$ , ta có:

${(\vec{a} + \vec{b})}^{2} = {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$ ;

${(\vec{a} - \vec{b})}^{2} = {\vec{a}}^{2} - 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$ ;

$(\vec{a} - \vec{b}) . (\vec{a} + \vec{b}) = {\vec{a}}^{2} - {\vec{b}}^{2}$ .

Lời giải:

+ Ta có:

${(\vec{a} + \vec{b})}^{2} = (\vec{a} + \vec{b}) . (\vec{a} + \vec{b})$ (bình phương vô hướng của vectơ $\vec{a} + \vec{b}$ )

$= \vec{a} . \vec{a} + \vec{a} . \vec{b} + \vec{b} . \vec{a} + \vec{b} . \vec{b}$

$= {\vec{a}}^{2} + \vec{a} . \vec{b} + \vec{a} . \vec{b} + {\vec{b}}^{2}$ (áp dụng tính chất giao hoán)

$= {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$

Vậy ${(\vec{a} + \vec{b})}^{2} = {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$ .

+ Ta có:

${(\vec{a} - \vec{b})}^{2} = (\vec{a} - \vec{b}) . (\vec{a} - \vec{b})$ (bình phương vô hướng của vectơ $\vec{a} - \vec{b}$ )

$= \vec{a} . \vec{a} - \vec{a} . \vec{b} - \vec{b} . \vec{a} + (- \vec{b}) . (- \vec{b})$

$= {\vec{a}}^{2} - \vec{a} . \vec{b} - \vec{a} . \vec{b} + {\vec{b}}^{2}$ (áp dụng tính chất giao hoán)

$= {\vec{a}}^{2} - 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$

Vậy ${(\vec{a} - \vec{b})}^{2} = {\vec{a}}^{2} - 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$ .

+ Ta có:

$(\vec{a} - \vec{b}) (\vec{a} + \vec{b})$ $= \vec{a} . \vec{a} + \vec{a} . \vec{b} + (- \vec{b}) . \vec{a} + (- \vec{b}) . \vec{b}$

$= {\vec{a}}^{2} + \vec{a} . \vec{b} - \vec{a} . \vec{b} - \vec{b} . \vec{b}$ (áp dụng tính chất giao hoán)

$= {\vec{a}}^{2} - {\vec{b}}^{2}$ .

Vậy $(\vec{a} - \vec{b}) . (\vec{a} + \vec{b}) = {\vec{a}}^{2} - {\vec{b}}^{2}$ .

3. Một số ứng dụng

Luyện tập 4 trang 96 Toán lớp 10: Sử dụng tích vô hướng, chứng minh minh định lí Pythagore: Tam giác ABC vuông tại A khi và chỉ khi BC² = AB² + AC²

Lời giải:

+ Ta chứng minh định lí thuận:

Có tam giác ABC vuông ở A, cần chứng minh BC² = AB² + AC².

Sử dụng tích vô hướng, chứng minh minh định lí Pythagore: Tam giác ABC vuông tại A khi và chỉ khi

Tam giác ABC vuông tại A nên $\hat{B A C} = 90 °$ .

Ta có: ${\vec{B C}}^{2} = {(\vec{A C} - \vec{A B})}^{2} = {\vec{A C}}^{2} + {\vec{A B}}^{2} - 2 \vec{A C} . \vec{A B}$

Suy ra: BC² = AC² + AB² – 2 . AC . AB . cos $(\vec{A C}, \vec{A B})$

= AB² + AC² – 2 . AC . AB . cosA

= AB² + AC² – 2 . AC . AB . cos 90°

= AB² + AC² – 2 . AC . AB . 0

= AB² + AC².

Vậy BC² = AB² + AC².

+ Ta chứng minh định lí đảo:

Cho tam giác ABC có BC² = AB² + AC² thì tam giác ABC vuông tại A.

Sử dụng tích vô hướng, chứng minh minh định lí Pythagore: Tam giác ABC vuông tại A khi và chỉ khi

Ta có: ${\vec{B C}}^{2} = {(\vec{A C} - \vec{A B})}^{2} = {\vec{A C}}^{2} + {\vec{A B}}^{2} - 2 \vec{A C} . \vec{A B}$

Suy ra: BC² = AC² + AB² – 2 . AC . AB . cos $(\vec{A C}, \vec{A B})$ (*)

Mà theo giả thiết ta có: BC² = AB² + AC² nên thay vào (*) ta được:

BC² = BC² – 2 . AC . AB . cos $(\vec{A C}, \vec{A B})$

Suy ra: 2 . AC . AB . cos $(\vec{A C}, \vec{A B})$ = 0

$\Leftrightarrow \cos (\vec{A C}, \vec{A B}) = 0$ hay $\cos \hat{B A C} = 0$

Do đó: $\hat{B A C} = 90 °$ .

Vậy tam giác ABC vuông tại A.

Bài tập

Giải Toán 10 trang 97 Tập 1

Bài 1 trang 97 Toán lớp 10: Nếu hai điểm M, N thỏa mãn $\vec{M N} . \vec{N M} = - 4$ thì độ dài đoạn thẳng MN bằng bao nhiêu?

A. MN = 4;

B. MN = 2;

C. MN = 16;

D. MN = 256.

Lời giải:

Đáp án đúng là: B.

Ta có:

$\vec{M N} . \vec{N M} = \vec{M N} . (- \vec{M N}) = - (\vec{M N} . \vec{M N}) = - {\vec{M N}}^{2} = - M N^{2}$

Lại có: $\vec{M N} . \vec{N M} = - 4$ , do đó: – MN² = – 4 ⇔ MN² = 4.

Suy ra MN = 2 (MN là độ dài đoạn thẳng nên MN > 0).

Vậy MN = 2.

Giải Toán 10 trang 98 Tập 1

Bài 2 trang 98 Toán lớp 10: Phát biểu nào sau đây là đúng?

A. Nếu $\vec{a}, \vec{b}$ khác $\vec{0}$ và $(\vec{a}, \vec{b}) < 90 °$ thì $\vec{a} . \vec{b} < 0;$

B. Nếu $\vec{a}, \vec{b}$ khác $\vec{0}$ và $(\vec{a}, \vec{b}) > 90 °$ thì $\vec{a} . \vec{b} > 0$

C. Nếu $\vec{a}, \vec{b}$ khác $\vec{0}$ và $(\vec{a}, \vec{b}) < 90 °$ thì $\vec{a} . \vec{b} > 0$

D. Nếu $\vec{a}, \vec{b}$ khác $\vec{0}$ và $(\vec{a}, \vec{b}) \neq 90 °$ thì $\vec{a} . \vec{b} < 0.$

Lời giải:

Đáp án đúng là: C.

Với $\vec{a}, \vec{b}$ khác $\vec{0}$ thì $(\vec{a}, \vec{b}) < 90 °$ $\Rightarrow \cos (\vec{a}, \vec{b}) > 0$

Do đó ta có: $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b}) > 0$ .

Vậy $\vec{a}, \vec{b}$ khác $\vec{0}$ và $(\vec{a}, \vec{b}) < 90 °$ thì $\vec{a} . \vec{b} > 0$ .

Bài 3 trang 98 Toán lớp 10: Tính $\vec{a} . \vec{b}$ trong mỗi trường hợp sau:

a) $|\vec{a}| = 3, |\vec{b}| = 4, (\vec{a}, \vec{b}) = 30 °$ ;

b) $|\vec{a}| = 5, |\vec{b}| = 6, (\vec{a}, \vec{b}) = 120 °$ ;

c) $|\vec{a}| = 2, |\vec{b}| = 3,$ $\vec{a}$ và $\vec{b}$ cùng hướng;

d) $|\vec{a}| = 2, |\vec{b}| = 3,$ $\vec{a}$ và $\vec{b}$ ngược hướng.

Lời giải:

a) Ta có: $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b})$ = 3 . 4 cos 30° = $6 \sqrt{3}$ .

b) Ta có: $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b})$ = 5 . 6 cos 120° = – 15.

c) Hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng nên

$\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| = 2 . 3 = 6$ .

d) Hai vectơ $\vec{a}$ và $\vec{b}$ ngược hướng nên

$\vec{a} . \vec{b} = - (|\vec{a}| . |\vec{b}|) = - (2 . 3) = - 6$ .

Bài 4 trang 98 Toán lớp 10: Cho hình vuông ABCD cạnh a. Tính các tích vô hướng sau:

a) $\vec{A B} . \vec{A C}$ ;

b) $\vec{A C} . \vec{B D}$ .

Lời giải:

Cho hình vuông ABCD cạnh a. Tính các tích vô hướng sau

a) Xét hình vuông ABCD có:

AC² = AB² + BC² = a² + a² = 2a² (định lí py – ta – go)

⇒ AC= $a \sqrt{2}$

Ta lại có đường chéo AC là tia phân giác của $\hat{B A D}$ .

Do đó: $\hat{B A C} = \frac{1}{2} \hat{B A D} = \frac{1}{2} .90 ° = 45 °$ .

Ta có:

$\vec{A B} . \vec{A C} = |\vec{A B}| . |\vec{A C}| . \cos (\vec{A B}, \vec{A C})$

$= A B . A C . \cos \hat{B A C}$

$= a . a \sqrt{2} . c o s 45^{\circ}$

=a²

Vậy $\vec{A B} . \vec{A C} {=a}^{2}$

b) ABCD là hình vuông nên hai đường chéo AC và BD vuông góc với nhau.

Do đó: $\vec{A C} ⊥ \vec{B D}$ , nên $\vec{A C} . \vec{B D} = 0$ .

Bài 5 trang 98 Toán lớp 10: Cho tam giác ABC. Chứng minh:

$A B^{2} + \vec{A B} . \vec{B C} + \vec{A B} . \vec{C A} = 0$

Lời giải:

Cho tam giác ABC. Chứng minh AB^2 + vectơ AB. vectơ BC + vectơ AB. vectơ CA =0

Ta có:

$A B^{2} + \vec{A B} . \vec{B C} + \vec{A B} . \vec{C A}$

$= A B^{2} + \vec{A B} . (\vec{B C} + \vec{C A})$

$= A B^{2} + \vec{A B} . \vec{B A}$

$= A B^{2} + \vec{A B} . (- \vec{A B})$

$= A B^{2} - {\vec{A B}}^{2}$

$= A B^{2} - A B^{2} = 0$ .

Vậy $A B^{2} + \vec{A B} . \vec{B C} + \vec{A B} . \vec{C A} = 0$ .

Bài 6 trang 98 Toán lớp 10: Cho tam giác nhọn ABC, kẻ đường cao AH. Chứng minh rằng:

a) $\vec{A B} . \vec{A H} = \vec{A C} . \vec{A H}$ ;

b) $\vec{A B} . \vec{B C} = \vec{H B} . \vec{B C}$ .

Lời giải:

Tam giác ABC nhọn nên H thuộc cạnh BC.

Cho tam giác nhọn ABC, kẻ đường cao AH. Chứng minh rằng

a) Do AH là đường cao của tam giác ABC nên AH ⊥ CB.

Do đó: $\vec{A H} . \vec{C B} = 0$ .

Ta có: $\vec{A B} . \vec{A H} - \vec{A C} . \vec{A H}$

$= \vec{A H} . \vec{A B} - \vec{A H} . \vec{A C}$ (tính chất giao hoán)

$= \vec{A H} . (\vec{A B} - \vec{A C})$

$= \vec{A H} . \vec{C B} = 0$

Do đó:

$\vec{A B} . \vec{A H} - \vec{A C} . \vec{A H} = 0$

$\Leftrightarrow \vec{A B} . \vec{A H} = \vec{A C} . \vec{A H}$

Vậy $\vec{A B} . \vec{A H} = \vec{A C} . \vec{A H}$ .

b) Ta có:

$\vec{A B} . \vec{B C} - \vec{H B} . \vec{B C}$

$= \vec{B C} . \vec{A B} - \vec{B C} . \vec{H B}$ (tính chất giao hoán)

$= \vec{B C} . (\vec{A B} - \vec{H B})$

$= \vec{B C} . (\vec{A B} - (- \vec{B H}))$

$= \vec{B C} . (\vec{A B} + \vec{B H})$

$= \vec{B C} . \vec{A H} = 0$

Suy ra:

$\vec{A B} . \vec{B C} - \vec{H B} . \vec{B C} = 0$

$\Leftrightarrow \vec{A B} . \vec{B C} = \vec{H B} . \vec{B C}$

Vậy $\vec{A B} . \vec{B C} = \vec{H B} . \vec{B C}$ .

Bài 7 trang 98 Toán lớp 10: Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 700 km/h thì gặp luồng gió thổi từ hướng đông bắc sang hướng tây nam với tốc độ 40 km/h (Hình 68). Máy bay bị thay đổi vận tốc sau khi gặp gió thổi.

Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần trăm theo đơn vị km/h).

Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 700 km/h thì gặp luồng gió thổi

Lời giải:

Giả sử vận tốc của máy bay theo hướng đông sang tây là $\vec{v_{1}}$ , vận tốc của luồng gió theo hướng đông bắc sang tây nam là $\vec{v_{2}}$ và vận tốc mới của máy bay chính là $\vec{v}$ thỏa mãn $\vec{v} = \vec{v_{1}} + \vec{v_{2}}$ . Ta cần tính độ dài vectơ $\vec{v}$ .

Theo bài ra ta có: $|\vec{v_{1}}| = 700$ km/h, $|\vec{v_{2}}| = 40$ km/h, $(\vec{v_{1}}, \vec{v_{2}}) = 45 °$ .

Biểu diễn bài toán như hình vẽ dưới đây:

Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 700 km/h thì gặp luồng gió thổi

Khi đó ta có: ABCD là hình bình hành có $\hat{A B C} = 45 °$ .

Suy ra: $\hat{D A B} = 180 ° - 45 ° = 135 °$ ; $A D = |\vec{v_{2}}| = 40$ , $A B = |\vec{v_{1}}| = 700$ .

Ta cần tính độ dài đoạn thẳng BD, đây chính là độ dài vectơ $\vec{v}$ .

Áp dụng định lí sin trong tam giác ABD, ta có:

BD²= AD² + AB² – 2 . AD . AB . cosA

= 40² + 700² – 2 . 40 . 700 . cos135°

≈ 531 197, 98

Suy ra BD ≈ 728,83 (km/h).

Vậy tốc độ mới của máy bay sau khi gặp gió thổi là 728,83 km/h.

Bài 8 trang 98 Toán lớp 10: Cho tam giác ABC có AB = 2, AC = 3, $\hat{B A C} = 60 °$ . Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn $\vec{A D} = \frac{7}{12} \vec{A C}$ .

a) Tính $\vec{A B} . \vec{A C}$ .

b) Biểu diễn $\vec{A M}, \vec{B D}$ theo $\vec{A B}, \vec{A C}$ .

c) Chứng minh AM ⊥ BD.

Lời giải:

Cho tam giác ABC có AB = 2, AC = 3, góc BAC = 60 độ . Gọi M là trung điểm của đoạn thẳng BC

a) Ta có: $\vec{A B} . \vec{A C} = |\vec{A B}| . |\vec{A C}| . \cos (\vec{A B}, \vec{A C})$

$= A B . A C . c o s \hat{B A C}$ = 2 . 3 . cos60° = 3.

b) + Do M là trung điểm của BC nên với điểm A ta có:

$\vec{A B} + \vec{A C} = 2 \vec{A M}$

$\Rightarrow \vec{A M} = \frac{1}{2} (\vec{A B} + \vec{A C})$

$= \frac{1}{2} \vec{A B} + \frac{1}{2} \vec{A C}$

Do đó: $\vec{A M} = \frac{1}{2} \vec{A B} + \frac{1}{2} \vec{A C}$ .

+ Ta có: $\vec{B D} = \vec{B A} + \vec{A D} = (- \vec{A B}) + \vec{A D}$

Mà $\vec{A D} = \frac{7}{12} \vec{A C}$

Nên

$\vec{B D} = (- \vec{A B}) + \frac{7}{12} \vec{A C}$

$= - \vec{A B} + \frac{7}{12} \vec{A C}$

Vậy $\vec{B D} = - \vec{A B} + \frac{7}{12} \vec{A C}$ .

c) Ta có:

$\vec{A M} . \vec{B D} = (\frac{1}{2} \vec{A B} + \frac{1}{2} \vec{A C}) . (- \vec{A B} + \frac{7}{12} \vec{A C})$

$= \frac{- 1}{2} {\vec{A B}}^{2} + \frac{7}{24} \vec{A B} . \vec{A C} - \frac{1}{2} \vec{A C} . \vec{A B} + \frac{7}{24} {\vec{A C}}^{2}$

$= \frac{- 1}{2} . A B^{2} + \frac{7}{24} . \vec{A B} . \vec{A C} - \frac{1}{2} \vec{A B} . \vec{A C} + \frac{7}{24} . A C^{2}$

$= \frac{- 1}{2} {.2}^{2} + \frac{7}{24} .3 - \frac{1}{2} .3 + \frac{7}{24} {.3}^{2}$ = 0

Suy ra: $\vec{A M} . \vec{B D} = 0$ .

Vậy AM ⊥ BD.

Lý thuyết Tích vô hướng của hai vectơ

1. Định nghĩa

1.1. Tích vô hướng của hai vectơ có cùng điểm đầu

– Góc giữa hai vectơ $\vec{OA}$ , $\vec{OB}$ là góc giữa hai tia OA, OB và được kí hiệu là $(\vec{OA}, \vec{OB})$

– Tích vô hướng của hai vectơ $\vec{OA}$ và $\vec{OB}$ là một số thực, kí hiệu là $\vec{OA}$ . $\vec{OB}$ , được xác định bởi công thức: $\vec{OA} . \vec{OB} = |\vec{OA}| . |\vec{OB}| . \cos (\vec{OA}, \vec{OB})$ .

Ví dụ: Cho tam giác ABC đều cạnh 2a có đường cao AH. Tính tích vô hướng của $\vec{AB} . \vec{AC}$ .

Hướng dẫn giải:

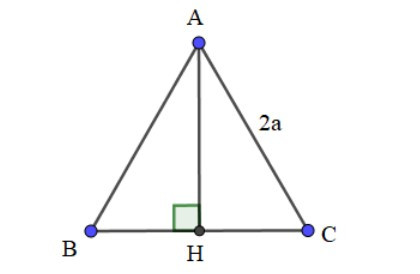
Tích vô hướng của hai vectơ (Lý thuyết + Bài tập Toán lớp 10) – Cánh diều (ảnh 1)

Vì tam giác ABC đều nên $\hat{BAC}$ = 60°

⇒ $(\vec{AB}, \vec{AC})$ = $\hat{BAC}$ = 60°

Ta có:

$\vec{AB} . \vec{AC}$ = $|\vec{AB}| . |\vec{AC}| . \cos (\vec{AB}, \vec{AC})$

⇒ $\vec{AB} . \vec{AC}$ = AB.AC.cos $\hat{BAC}$ = AB.AC.cos60° = 2a.2a. $\frac{1}{2}$ = 2a².

1.2. Tích vô hướng của hai vectơ tùy ý

Định nghĩa:

Cho hai vectơ $\vec{a}$ , $\vec{b}$ khác $\vec{0} .$ Lấy một điểm O và vẽ vectơ $\vec{OA} = \vec{a}, \vec{OB} = \vec{b}$ (Hình vẽ).

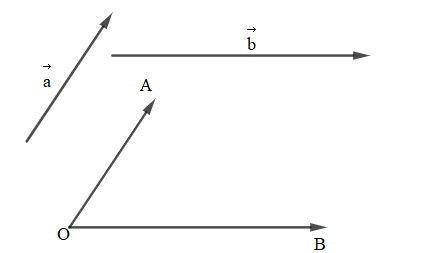
Tích vô hướng của hai vectơ (Lý thuyết + Bài tập Toán lớp 10) – Cánh diều (ảnh 1)

+ Góc giữa hai vectơ $\vec{a}$ , $\vec{b}$ , kí hiệu $(\vec{a}, \vec{b})$ , là góc giữa hai vectơ $\vec{OA}$ , $\vec{OB}$ .

+ Tích vô hướng của hai vectơ $\vec{a}$ và $\vec{b}$ , kí hiệu $\vec{a}$ . $\vec{b}$ là tích vô hướng của hai vectơ $\vec{OA}$ và $\vec{OB}$ . Như vậy, tích vô hướng của hai vectơ $\vec{a}$ và $\vec{b}$ là một số thực được xác định bởi công thức: $\vec{a}$ . $\vec{b}$ = $|\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b})$ .

Quy ước: Tích vô hướng của một vectơ bất kì với vectơ $\vec{0}$ là số 0.

Chú ý:

+) $(\vec{a}, \vec{b})$ = $(\vec{b}, \vec{a})$

+) Nếu $(\vec{a}, \vec{b})$ = 90° thì ta nói hai vectơ $\vec{a}$ , $\vec{b}$ vuông góc với nhau, kí hiệu $\vec{a}$ ⊥ $\vec{b}$ hoặc $\vec{b}$ ⊥ $\vec{a}$ . Khi đó $\vec{a}$ . $\vec{b}$ = $|\vec{a}| . |\vec{b}| . \cos 90 °$ = 0.

+) Tích vô hướng của hai vectơ cùng hướng bằng tích hai độ dài của chúng.

+) Tích vô hướng của hai vectơ ngược hướng bằng số đối của tích hai độ dài của chúng.

Ví dụ: Cho tam giác vuông cân ABC có AB = AC = a. Tính các tích vô hướng $\vec{AB} . \vec{AC}$ , $\vec{AC} . \vec{CB}$ .

Hướng dẫn giải:

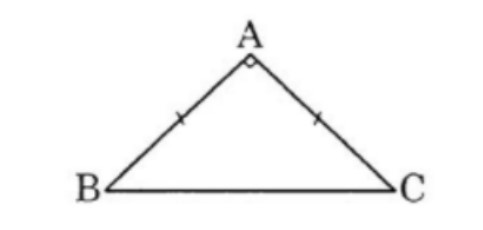
Tích vô hướng của hai vectơ (Lý thuyết + Bài tập Toán lớp 10) – Cánh diều (ảnh 1)

+ Vì tam giác ABC vuông cân, mà AB = AC

⇒ Tam giác ABC vuông cân tại A.

⇒ AB ⊥ AC

⇒ $\vec{AB} . \vec{AC}$ = $|\vec{AB}| . |\vec{AC}| . \cos 90 °$ = $|\vec{AB}| . |\vec{AC}| .0$ = 0

+ Ta có: BC = $\sqrt{{AB}^{2} + {AC}^{2}}$ = $\sqrt{a^{2} + a^{2}}$ = a $\sqrt{2}$ .

⇒ $\vec{AC} . \vec{CB}$ = $|\vec{AC}| . |\vec{CB}| . \cos (\vec{AC}, \vec{CB})$ = a. a $\sqrt{2}$ .cos135° = a. a $\sqrt{2}$ . $(\frac{- \sqrt{2}}{2})$ = –a².

2. Tính chất

Với hai vectơ bất kì $\vec{a}$ , $\vec{b}$ và số thực k tùy ý, ta có:

+) $\vec{a}$ . $\vec{b}$ = $\vec{b}$ . $\vec{a}$ (tính chất giao hoán);

+) $\vec{a} . (\vec{b} + \vec{c}) = \vec{a} . \vec{b} + \vec{a} . \vec{c}$ (tính chất phân phối);

+) $(k \vec{a}) \vec{b} = k (\vec{a} . \vec{b}) = \vec{a} . (k \vec{b})$ ;

+) ${\vec{a}}^{2}$ ≥ 0, ${\vec{a}}^{2}$ = 0 ⟺ $\vec{a}$ = $\vec{0}$ .

Trong đó, kí hiệu $\vec{a}$ . $\vec{a}$ = ${\vec{a}}^{2}$ và biểu thức này được gọi là bình phương vô hướng của vectơ $\vec{a}$ .

Ví dụ: Cho 4 điểm A, B, C, D bất kì. Chứng minh: $\vec{AB} . \vec{CD} + \vec{BC} . \vec{AD} + \vec{CA} . \vec{BD} = 0$ .

Hướng dẫn giải:

Ta có:

$\vec{AB} . \vec{CD}$ = $\vec{AB} . (\vec{CA} + \vec{AD})$ = $\vec{AB} . \vec{CA} + \vec{AB} . \vec{AD}$ (tính chất phân phối)

$\vec{BC} . \vec{AD}$ = $(\vec{BA} + \vec{AC}) . \vec{AD}$ = $\vec{BA} . \vec{AD} + \vec{AC} . \vec{AD}$ = $- \vec{AB} . \vec{AD} + \vec{AC} . \vec{AD}$ (tính chất phân phối)

$\vec{CA} . \vec{BD}$ = $\vec{CA} . (\vec{BA} + \vec{AD})$ = $\vec{CA} . \vec{BA} + \vec{CA} . \vec{AD}$ = $- \vec{CA} . \vec{AB} - \vec{AC} . \vec{AD}$ (tính chất phân phối)

$\Rightarrow \vec{AB} . \vec{CD} + \vec{BC} . \vec{AD} + \vec{CA} . \vec{BD}$

$= \vec{AB} . \vec{CA} + \vec{AB} . \vec{AD} - \vec{AB} . \vec{AD} + \vec{AC} . \vec{AD} - \vec{CA} . \vec{AB} - \vec{AC} . \vec{AD}$

= $(\vec{AB} . \vec{CA} - \vec{CA} . \vec{AB}) + (\vec{AB} . \vec{AD} - \vec{AB} . \vec{AD}) + (\vec{AC} . \vec{AD} - \vec{AC} . \vec{AD})$ (tính chất giao hoán và kết hợp)

= 0

⟺ $\vec{AB} . \vec{CD} + \vec{BC} . \vec{AD} + \vec{CA} . \vec{BD} = 0$ (đpcm).

3. Một số ứng dụng

3.1. Tính độ dài của đoạn thẳng

Nhận xét:

Với hai điểm A, B phân biệt, ta có: ${\vec{AB}}^{2} = {|\vec{AB}|}^{2}$ .

Do đó độ dài đoạn thẳng AB được tính như sau: AB = $\sqrt{{\vec{AB}}^{2}}$

3.2. Chứng minh hai đường thẳng vuông góc

Nhận xét:

+ Cho hai vectơ bất kì $\vec{a}$ và $\vec{b}$ khác vectơ $\vec{0}$ . Ta có: $\vec{a}$ . $\vec{b}$ = 0 ⟺ $\vec{a}$ ⊥ $\vec{b}$ .

Hai đường thẳng AB và CD vuông góc với nhau khi và chỉ khi $\vec{AB} . \vec{CD} = 0.$ + Hai đường thẳng a và b vuông góc khi và chỉ khi $\vec{u} . \vec{v} = 0$ , trong đó $\vec{u}$ ≠ 0, $\vec{v}$ ≠ 0, giá của vectơ $\vec{u}$ song song hoặc trùng với đường thẳng a và giá của vectơ $\vec{v}$ song song hoặc trùng với đường thẳng b.

Ví dụ: Cho hai vectơ $\vec{a}$ và $\vec{b}$ vuông góc với nhau và $|\vec{a}| = 1$ , $|\vec{b}| = \sqrt{2}$ . Chứng minh hai vectơ 2 $\vec{a}$ – $\vec{b}$ và $\vec{a}$ + $\vec{b}$ vuông góc với nhau.

Hướng dẫn giải:

Vì $\vec{a}$ và $\vec{b}$ vuông góc với nhau ⟺ $\vec{a}$ . $\vec{b}$ = 0

Ta có:

$(2 \vec{a} - \vec{b}) (\vec{a} + \vec{b})$ = $2 {\vec{a}}^{2} + 2 \vec{a} . \vec{b} - \vec{a} . \vec{b} - {\vec{b}}^{2}$ = $2 {\vec{a}}^{2} + \vec{a} . \vec{b} - {\vec{b}}^{2}$ = $2 {|\vec{a}|}^{2} + \vec{a} . \vec{b} - {|\vec{b}|}^{2}$