Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài tập cuối chương 4 chi tiết sách Toán 10 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài tập cuối chương 4

Giải Toán 10 trang 99 Tập 1

Bài 1 trang 99 Toán lớp 10: Cho tam giác ABC có AB = 3, AC = 4, $\widehat{BAC}=120°$. Tính (làm tròn kết quả đến hàng đơn vị):

a) Độ dài cạnh BC và độ lớn góc B;

b) Bán kính đường tròn ngoại tiếp;

c) Diện tích của tam giác;

d) Độ dài đường cao xuất phát từ A;

e) $\overrightarrow{AB}.\overrightarrow{AC},\overrightarrow{AM}.\overrightarrow{BC}$ với M là trung điểm của BC.

Lời giải:

a) + Áp dụng định lí côsin trong tam giác ABC ta có:

BC2 = AB2 + AC­2 – 2 . AB . AC . cos$\widehat{BAC}$

        = 32 + 42 – 2 . 3. 4 . cos 120°

        = 9 + 16 – (– 12)

        = 37

Suy ra: $BC=\sqrt{37}\approx 6$.

+ Ta có: $\cos B=\frac{A{B}^2+B{C}^2-A{C}^2}{2.AB.BC}$$=\frac{3^2+6^2-4^2}{\mathrm{2.3.6}}=\frac{29}{36}$

Suy ra $\widehat{B}\approx 36°$.

b) Áp dụng định lí sin trong tam giác ABC ta có: $\frac{BC}{\sin A}=2R$

Suy ra: $R=\frac{BC}{2\sin A}=\frac{6}{2.\sin 120°}=2\sqrt{3}\approx 3$.

Vậy bán kính đường tròn ngoại tiếp tam giác ABC là R ≈ 3.

c) Diện tích tam giác ABC là:

$S=\frac{1}{2}AB.AC.\sin A$$=\frac{1}{2}\mathrm{.3.4.}\sin 120°=3\sqrt{3}\approx 5$.

d) Kẻ đường cao AH.

Ta có diện tích tam giác ABC là: $S=\frac{1}{2}AH.BC$

Suy ra: $AH=\frac{2S}{BC}=\frac{2.5}{6}\approx 2$.

e)

+ Ta có:

$\overrightarrow{AB}.\overrightarrow{AC}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|.\cos \left(\overrightarrow{AB},\overrightarrow{AC}\right)$

$=AB.AC.\cos \widehat{BAC}$

= 3 . 4 . cos 120° = – 6.

Do đó: $\overrightarrow{AB}.\overrightarrow{AC}=-6$.

+ Do M là trung điểm của BC nên ta có: $\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}$.

Suy ra: $\overrightarrow{AM}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)$.

Khi đó: $\overrightarrow{AM}.\overrightarrow{BC}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right).\overrightarrow{BC}$

$=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right).\left(\overrightarrow{BA}+\overrightarrow{AC}\right)$

$=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right).\left(\left(-\overrightarrow{AB}\right)+\overrightarrow{AC}\right)$

$=\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{AB}\right).\left(\overrightarrow{AC}-\overrightarrow{AB}\right)$

$=\frac{1}{2}\left({\overrightarrow{AC}}^2-{\overrightarrow{AB}}^2\right)$

$=\frac{1}{2}\left(AC-AB\right)=\frac{1}{2}\left(4-3\right)=\frac{1}{2}$

Vậy $\overrightarrow{AM}.\overrightarrow{BC}=\frac{1}{2}$

Bài 2 trang 99 Toán lớp 10: Không dùng máy tính cầm tay, hãy tính giá trị của các biểu thức sau:

A = (sin 20° + sin 70°)² + (cos 20° + cos 110°)², 

B = tan 20° + cot 20° + tan 110° + cot 110°.

Lời giải:

+ Ta có: 

A = (sin 20° + sin 70°)² + (cos 20° + cos 110°)²

= [sin(90° – 70°) + sin 70°]² + [cos(90° – 70°) + cos(180° – 70°)]²

= (cos70° + sin 70°)² + [sin 70° + (– cos 70°)]²

= (cos 70° + sin 70°)² + (sin 70° – cos 70°)²

= cos² 70° + 2 . cos 70° . sin 70° + sin² 70° + sin² 70° – 2 . sin 70° . cos 70° + cos² 70°

= 2(cos² 70° + sin² 70°) 

= 2 . 1 = 2

Vậy A = 2. 

+ Ta có: 

B = tan 20° + cot 20° + tan 110° + cot 110°

= tan (90° – 70°) + cot(90° – 70°) + tan (180° – 70°) + cot (180° – 70°)

= cot 70° + tan 70° + (– tan 70°) + (– cot 70°)

= (cot 70° – cot 70°) + (tan 70° – tan 70°)

= 0 + 0 = 0 

Vậy B = 0. 

Bài 3 trang 99 Toán lớp 10: Không dùng thước đo góc, làm thế nào để biết số đo góc đó.

Bạn Hoài vẽ góc xOy và đố bạn Đông làm thế nào để có thể biết được số đo góc của góc này khi không có thước đo góc. Bạn Đông làm như sau: (Hình 70)

- Chọn các điểm A, B lần lượt thuộc các tia Ox và Oy sao cho OA = OB = 2 cm; 

- Đo độ dài đoạn thẳng AB được AB = 3,1 cm. 

Từ các dữ kiện trên bạn Đông tính được cos$\widehat{xOy}$, từ đó suy ra độ lớn góc xOy. 

Em hãy cho biết số đo góc xOy ở Hình 69 bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị).

Lời giải:

* Tính góc xOy bạn Hoài vẽ:  

Áp dụng hệ quả của định lí côsin trong tam giác ABO ta có: 

$$\begin{gathered} \cos O=\frac{O{A}^2+O{B}^2-A{B}^2}{2.OA.OB} \\ =\frac{2^2+2^2-{\left(3,1\right)}^2}{\mathrm{2.2.2}} \\ =-\frac{161}{800} \end{gathered}$$

Do đó: $\widehat{O}\approx 102°$. 

Vậy từ các dự kiện bạn Đông tính được, ta suy ra $\widehat{xOy}\approx 102°$. 

Bài 4 trang 99 Toán lớp 10: Có hai trạm quan sát A và B ven hồ và một trạm quan sát C ở giữa hồ. Để tính khoảng cách từ A và từ B đến C, người ta làm như sau (Hình 71):

- Đo góc BAC được 60°, đo góc ABC được 45°; 

- Đo khoảng cách AB được 1 200 m. 

Khoảng cách từ trạm C đến các trạm A và B bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)? 

Lời giải:

Ba vị trí A, B, C tạo thành 3 đỉnh của tam giác ABC. 

Ta có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong tam giác ABC) 

Suy ra: $\widehat{C}=180°-\left(\widehat{A}+\widehat{B}\right)=180°-\left(60°+45°\right)=75°$. 

Áp dụng định lí sin trong tam giác ABC ta có: $\frac{AB}{\sin C}=\frac{BC}{\sin A}=\frac{AC}{\sin B}$

Do đó: $AC=\frac{AB.\sin B}{\sin C}=\frac{1200.\sin 45°}{\sin 75°}\approx 878$ (m); 

$BC=\frac{AB.\sin A}{\sin C}=\frac{1200.\sin 60°}{\sin 75°}\approx 1076$ (m). 

Vậy khoảng cách từ trạm C đến trạm A khoảng 878 m và từ trạm C đến trạm B khoảng 1 076 m. 

Bài 5 trang 99, 100 Toán lớp 10: Một người đứng ở bờ sông, muốn đo độ rộng của khúc sông chảy qua vị trí đang đứng (khúc sông tương đối thẳng, có thể xem hai bờ song song với nhau).

Từ vị trí đang đứng A, người đó đo được góc nghiêng α = 35° so với bờ sông tới một vị trí C quan sát được ở phía bờ bên kia. Sau đó di chuyển dọc bờ sông đến vị trí B cách A một khoảng d = 50 m và tiếp tục đo được góc nghiêng β = 65° so với bờ bên kia tới vị trí C đã chọn (Hình 72). Hỏi độ rộng của khúc sông chảy qua vị trí người đó đang đứng là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Lời giải:

Dựng AD vuông góc với hai bên bờ sông, khi đó AD là độ rộng của khúc sông chạy qua vị trí của người đó đang đứng. Ta cần tính khoảng cách AD. 

Xét tam giác ABC ta có: $\widehat{CAB}+\widehat{ACB}=65°$ (tính chất góc ngoài tại đỉnh B của tam giác)

Suy ra $\widehat{ACB}=65°-\widehat{CAB}=65°-35°=30°$. 

Lại có $\widehat{ABC}=180°-65°=115°$. 

Áp dụng định lí sin trong tam giác ABC ta có: $\frac{AB}{\sin \widehat{ACB}}=\frac{AC}{\sin \widehat{ABC}}$.

Suy ra $AC=\frac{AB.\sin \widehat{ABC}}{\sin \widehat{ACB}}=\frac{50.\sin 115°}{\sin 30°}\approx 90,6$. 

Ta có: $\widehat{DAC}=90°-35°=55°$. 

Tam giác ADC vuông tại D nên $\cos \widehat{DAC}=\frac{AD}{AC}$.

$\Rightarrow AD=AC.\cos \widehat{DAC}=90,6.\cos 55°\approx \mathrm{52,0}$ (m).

Vậy độ rộng của khúc sông chảy qua vị trí người đó đang đứng là 52,0 m. 

Giải Toán 10 trang 100 Tập 1

Bài 6 trang 100 Toán lớp 10: Để đo khoảng cách giữa hai vị trí M, N ở hai phía ốc đảo, người ta chọn vị trí O bên ngoài ốc đảo sao cho: O không thuộc đường thẳng MN; các khoảng cách OM, ON và góc MON là đo được (Hình 74). Sau khi đo, ta có OM = 200 m, ON = 500 m, $\widehat{MON}=135°$ .

Khoảng cách giữa hai vị trí M, N là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)? 

Lời giải:

Ba vị trí O, M, N tạo thành ba đỉnh của tam giác. 

Tam giác OMN có OM = 200 m, ON = 500 m và $\widehat{MON}=135°$. 

Áp dụng định lí côsin trong tam giác OMN ta có: 

MN² = OM² + ON² – 2 . OM . ON . cos$\widehat{MON}$

        = 200² + 500² – 2 . 200 . 500 . cos135°

≈ 431421 

Suy ra: MN ≈ 657 m.

Vậy khoảng cách giữa hai ví trí M, N khoảng 657 m.

Bài 7 trang 100 Toán lớp 10: Chứng minh:

a) Nếu ABCD là hình bình hành thì $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{CE}=\overrightarrow{AE}$ với E là điểm bất kì; 

b) Nếu I là trung điểm của đoạn thẳng AB thì $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{IN}=2\overrightarrow{MN}$ với M, N là hai điểm bất kì; 

c) Nếu G là trọng tâm của tam giác ABC thì $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}-3\overrightarrow{MN}=3\overrightarrow{NG}$ với M, N là hai điểm bất kì. 

Lời giải:

a) 

Vì ABCD là hình bình hành nên $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$. 

Với E là điểm bất kì ta có: 

$\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{CE}=\overrightarrow{AC}+\overrightarrow{CE}=\overrightarrow{AE}$. 

Vậy $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{CE}=\overrightarrow{AE}$ với E là điểm bất kì. 

b) 

Vì I là trung điểm của AB nên với điểm M bất kì ta có: $\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$. 

Do đó, với điểm N bất kì, ta có: 

$$\begin{gathered} \overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{IN}=2\overrightarrow{MI}+2\overrightarrow{IN} \\ =2\left(\overrightarrow{MI}+\overrightarrow{IN}\right)=2\overrightarrow{MN} \end{gathered}$$

Vậy $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{IN}=2\overrightarrow{MN}$ với M, N là hai điểm bất kì. 

c) 

Do G là trọng tâm của tam giác ABC nên với điểm M bất kì ta có: 

$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$. 

Khi đó với điểm N bất kì ta có: 

$$\begin{gathered} \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}-3\overrightarrow{MN}=3\overrightarrow{MG}-3\overrightarrow{MN} \\ =3\left(\overrightarrow{MG}+\left(-\overrightarrow{MN}\right)\right)=3\left(\overrightarrow{MG}+\overrightarrow{NM}\right) \\ =3\left(\overrightarrow{NM}+\overrightarrow{MG}\right)=3\overrightarrow{NG} \end{gathered}$$

Vậy $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}-3\overrightarrow{MN}=3\overrightarrow{NG}$ với M, N là hai điểm bất kì. 

Bài 8 trang 100 Toán lớp 10: Cho hình bình hành ABCD có AB = 4, AD = 6, $\widehat{BAD}=60°$ (Hình 74).

a) Biểu thị các vectơ $\overrightarrow{BD},\overrightarrow{AC}$ theo $\overrightarrow{AB},\overrightarrow{AD}$. 

b) Tính các tích vô hướng $\overrightarrow{AB}.\overrightarrow{AD},\overrightarrow{AB}.\overrightarrow{AC},\overrightarrow{BD}.\overrightarrow{AC}$. 

c) Tính độ dài các đường chéo BD, AC. 

Lời giải:

a) Ta có: $\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}=-\overrightarrow{AB}+\overrightarrow{AD}$. 

Do ABCD là hình bình hành nên $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$. 

b) Ta có: $\overrightarrow{AB}.\overrightarrow{AD}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AD}\right|.\cos \left(\overrightarrow{AB},\overrightarrow{AD}\right)$

$=AB.AD.\cos \widehat{BAD}$ = 4 . 6 . cos60° = 12. 

Do đó: $\overrightarrow{AB}.\overrightarrow{AD}=12$. 

Ta cũng có: $\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{AB}.\left(\overrightarrow{AB}+\overrightarrow{AD}\right)$

$={\overrightarrow{AB}}^2+\overrightarrow{AB}.\overrightarrow{AD}$ = AB² + 12 = 4² + 12 = 28. 

Do đó: $\overrightarrow{AB}.\overrightarrow{AC}=28$. 

Lại có: $\overrightarrow{BD}.\overrightarrow{AC}=\left(-\overrightarrow{AB}+\overrightarrow{AD}\right).\left(\overrightarrow{AB}+\overrightarrow{AD}\right)$

$=\left(\overrightarrow{AD}-\overrightarrow{AB}\right).\left(\overrightarrow{AD}+\overrightarrow{AB}\right)$

$={\overrightarrow{AD}}^2-{\overrightarrow{AB}}^2$

= AD² – AB² = 6² – 4² = 20. 

Vậy $\overrightarrow{BD}.\overrightarrow{AC}=20$

c) Áp dụng định lí côsin trong tam giác ABD có: 

BD² = AB² + AD² – 2 . AB . AD . cosA

        = 4² + 6² – 2 . 4 . 6 . cos 60° = 28

$\Rightarrow BD=\sqrt{28}=2\sqrt{7}$

Ta có:

$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$$\Rightarrow {\left(\overrightarrow{AC}\right)}^2={\left(\overrightarrow{AB}+\overrightarrow{AD}\right)}^2$

$\iff {\overrightarrow{AC}}^2={\overrightarrow{AB}}^2+2.\overrightarrow{AB}.\overrightarrow{AD}+{\overrightarrow{AD}}^2$

$\iff A{C}^2=A{B}^2+2\overrightarrow{AB}.\overrightarrow{AD}+A{D}^2$

Suy ra: AC² = 4² + 2 . 12 + 6² = 76

$\Rightarrow AC=\sqrt{76}=2\sqrt{19}$

Bài 9 trang 100 Toán lớp 10: Hai lực $\overrightarrow{F_1},\overrightarrow{F_2}$ cho trước cùng tác dụng lên một vật tại điểm O và tạo với nhau một góc $\left(\overrightarrow{F_1},\overrightarrow{F_2}\right)=\alpha$ làm cho vật di chuyển theo hướng từ O đến C (Hình 75). Lập công thức tính cường độ của hợp lực $\overrightarrow{F}$ làm cho vật di chuyển theo hướng từ O đến C (giả sử chỉ có đúng hai lực $\overrightarrow{F_1},\overrightarrow{F_2}$ làm cho vật di chuyển).

Lời giải:

Ta thấy, AOBC là hình bình hành. 

Do đó: $\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}$

Suy ra: $\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}$ (1).

Ta cần tính cường độ của hợp lực $\overrightarrow{F}$ hay chính là tính $\left|\overrightarrow{F}\right|$. 

Từ (1) suy ra ${\left(\overrightarrow{F}\right)}^2={\left(\overrightarrow{F_1}+\overrightarrow{F_2}\right)}^2$.

$\iff {\overrightarrow{F}}^2={\overrightarrow{F_1}}^2+2.\overrightarrow{F_1}.\overrightarrow{F_2}+{\overrightarrow{F_2}}^2$

$\iff {\left|\overrightarrow{F}\right|}^2={\left|\overrightarrow{F_1}\right|}^2+2.\overrightarrow{F_1}.\overrightarrow{F_2}+{\left|\overrightarrow{F_2}\right|}^2$ (2)

Ta lại có: $\overrightarrow{F_1}.\overrightarrow{F_2}=\left|\overrightarrow{F_1}\right|.\left|\overrightarrow{F_2}\right|.\cos \left(\overrightarrow{F_1},\overrightarrow{F_2}\right)$$=\left|\overrightarrow{F_1}\right|.\left|\overrightarrow{F_2}\right|.\cos \alpha$ (3).

Từ (2) và (3) suy ra: ${\left|\overrightarrow{F}\right|}^2={\left|\overrightarrow{F_1}\right|}^2+2.\left|\overrightarrow{F_1}\right|.\left|\overrightarrow{F_2}\right|.\cos \alpha +{\left|\overrightarrow{F_2}\right|}^2$

$\Rightarrow \left|\overrightarrow{F}\right|=\sqrt{{\left|\overrightarrow{F_1}\right|}^2+2.\left|\overrightarrow{F_1}\right|.\left|\overrightarrow{F_2}\right|.\cos \alpha +{\left|\overrightarrow{F_2}\right|}^2}$

Vậy công thức tính cường độ của hợp lực $\overrightarrow{F}$ làm cho vật di chuyển theo hướng từ O đến C là $\left|\overrightarrow{F}\right|=\sqrt{{\left|\overrightarrow{F_1}\right|}^2+2.\left|\overrightarrow{F_1}\right|.\left|\overrightarrow{F_2}\right|.\cos \alpha +{\left|\overrightarrow{F_2}\right|}^2}$.

Lý thuyết Toán 10 Chương 4: Hệ thức lượng trong tam giác. Vectơ

1. Giá trị lượng giác của một góc từ 0° đến 180°

1.1 Định nghĩa

       

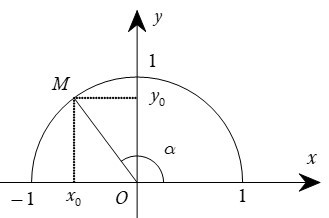
Với mỗi góc α (0 ≤ α ≤ 180°) ta xác định một điểm M (x₀, y₀) trên nửa đường tròn đơn vị sao cho góc $\widehat{\mathrm{xOM}}$= α. Khi đó ta có định nghĩa:

+) sin của góc α, kí hiệu là sinα, được xác định bởi: sinα = y₀;

+) côsin của góc α, kí hiệu là cosα, được xác định bởi: cosα = x₀;

+) tang của góc α, kí hiệu là tanα, được xác định bởi: tanα = $\frac{{\mathrm{y}}_0}{{\mathrm{x}}_0}$(x₀ ≠ 0);

+) côtang của góc α, kí hiệu là cotα, được xác định bởi: cotα = $\frac{{\mathrm{x}}_0}{{\mathrm{y}}_0}$(y₀ ≠ 0).

Các số sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của góc α.

Chú ý:

tanα = $\frac{\mathrm{sin\alpha }}{\mathrm{cos\alpha }}$(α ≠ 90°);

cotα = $\frac{\mathrm{cos\alpha }}{\mathrm{sin\alpha }}$(0 < α < 180°).

sin(90° – α) = cosα (0° ≤ α ≤ 90°);

cos(90° – α) = sinα (0° ≤ α ≤ 90°);

tan(90° – α) = cotα (0° ≤ α ≤ 90°);

cot(90° – α) = tanα (0° ≤ α ≤ 90°).

1.2. Tính chất

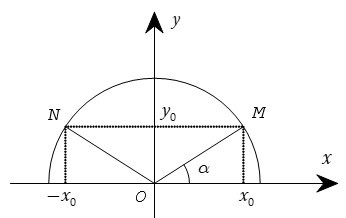
Trên hình bên ta có dây cung NM song song với trục Ox và nếu $\widehat{\mathrm{xOM}}$ = α thì $\widehat{\mathrm{xON}}$ = 180^o – α. Với 0° ≤ α ≤ 180° thì:

sin(180° – α) = sinα,

cos(180° – α) = – cosα,

tan(180° – α) = – tanα (α ≠ 90°),

cot(180° – α) = – cotα (α ≠ 0°, α ≠ 180°).

1.3. Giá trị lượng giác của các góc đặc biệt

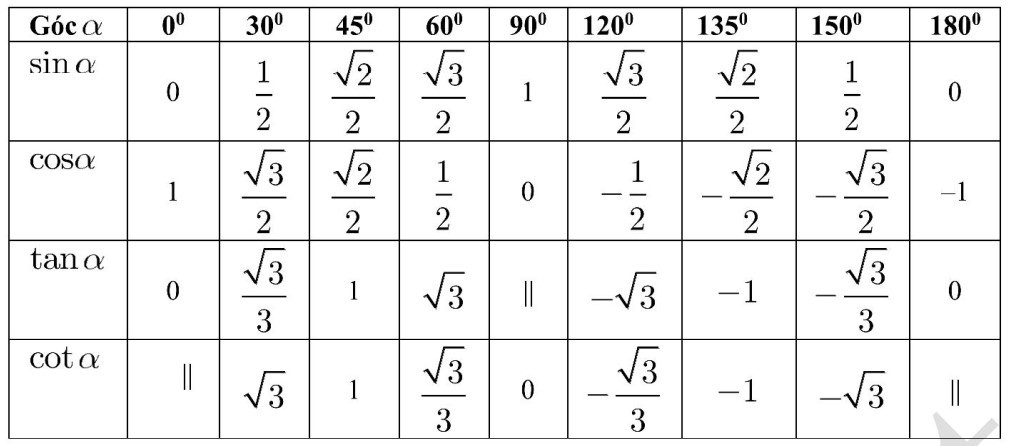
Chú ý: Cách sử dụng máy tính cầm tay để tính giá trị lượng giác:

– Ta có thể tìm giá trị lượng giác (đúng hoặc gần đúng) của một góc từ 0° đến 180° bằng cách sử dụng các phím: sin, cos, tan trên máy tính cầm tay.

2. Định lí côsin

Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó:

a² = b² + c² – 2bccosA,

b² = c² + a² – 2cacosB,

c² = a² + b² – 2abcosC.

Lưu ý:

cosA = $\frac{{\mathrm{b}}^2+{\mathrm{c}}^2-{\mathrm{a}}^2}{2\mathrm{bc}}$,

cosB = $\frac{{\mathrm{c}}^2+{\mathrm{a}}^2-{\mathrm{b}}^2}{2\mathrm{ca}}$,

cosC = $\frac{{\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2}{2\mathrm{ab}}$.

3. Định lí sin

Cho tam giác ABC có BC = a, CA = b, AB = c và bán kính đường tròn ngoại tiếp là R. Khi đó:

$\frac{\mathrm{a}}{\mathrm{sinA}}=\frac{\mathrm{b}}{\mathrm{sinB}}=\frac{\mathrm{c}}{\mathrm{sinC}}=2\mathrm{R}$

Lưu ý:

a = 2RsinA,

b = 2RsinB,

c = 2RsinC.

4. Tính diện tích tam giác

Công thức tính diện tích tam giác:

Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó, diện tích S của tam giác ABC là:

S = $\frac{1}{2}$bc.sinA = $\frac{1}{2}$ca.sin = $\frac{1}{2}$ab.sinC

Công thức Heron:

Công thức toán học Heron được sử dụng để tính diện tích của một tam giác theo độ dài ba cạnh như sau:

Cho tam giác ABC có BC = a, CA = b, AB = c, $\mathrm{p}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$. Khi đó, diện tích S của tam giác ABC là:

$\mathrm{S}=\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}$.

Trong đó p là nửa chu vi tam giác ABC.

5. Vectơ

Định nghĩa: Vectơ là một đoạn thẳng có hướng.

Vectơ có điểm đầu A, điểm cuối B được kí hiệu là $\overrightarrow{\mathrm{AB}}$ và đọc là “vectơ AB”. Để vẽ được vectơ $\overrightarrow{\mathrm{AB}}$ ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu nút B.

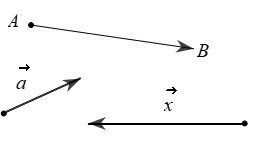
Đối với vectơ $\overrightarrow{\mathrm{AB}}$, ta gọi:

– Đường thẳng d đi qua hai điểm A và B là giá của vectơ $\overrightarrow{\mathrm{AB}}$.

– Độ dài đoạn thẳng AB là độ dài của vectơ $\overrightarrow{\mathrm{AB}}$, kí hiệu là $\left|\overrightarrow{\mathrm{AB}}\right|$.

Vectơ còn được kí hiệu là $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$, $\overrightarrow{\mathrm{x}}$, $\overrightarrow{\mathrm{y}}$ khi không cần chỉ rõ điểm đầu và điểm cuối của nó. Độ dài của vectơ $\overrightarrow{\mathrm{a}}$ được kí hiệu là $\left|\overrightarrow{\mathrm{a}}\right|$ 

Ví dụ: Vectơ $\overrightarrow{\mathrm{AB}}$ có độ dài là 5, ta có thể viết như sau: $\left|\overrightarrow{\mathrm{AB}}\right|$ = 5.

6. Vectơ cùng phương, vectơ cùng hướng

Định nghĩa:

– Hai vectơ cùng phương: Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

– Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng.

7. Hai vectơ bằng nhau

Hai vectơ $\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{CD}}$ bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu: $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{CD}}.$ 

Nhận xét:

– Hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu $\overrightarrow{\mathrm{a}}$ = $\overrightarrow{\mathrm{b}}$.

– Khi cho trước vectơ $\overrightarrow{\mathrm{a}}$ và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho $\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{a}}.$ 

8. Vectơ–không

Ta biết rằng mỗi vectơ có một điểm đầu và một điểm cuối và hoàn toàn được xác định khi biết điểm đầu và điểm cuối của nó.

Bây giờ với một điểm A bất kì ta quy ước có một vectơ đặc biệt mà điểm đầu và điểm cuối đều là A. Vectơ này được kí hiệu là $\left|\overrightarrow{0}\right|$ và được gọi là vectơ – không.

Định nghĩa: Vectơ–không là vectơ có điểm đầu và điểm cuối trùng nhau, kí hiệu là $\overrightarrow{0}$

Ta quy ước $\overrightarrow{0}$ cùng phương và cùng hướng với mọi vectơ và $\left|\overrightarrow{0}\right|$ = 0.

Nhận xét: Hai điểm A, B trùng nhau khi và chỉ khi $\overrightarrow{\mathrm{AB}}$= $\overrightarrow{0}$.

9. Tổng của hai vectơ

9.1. Định nghĩa

– Với ba điểm bất kì A, B, C, vectơ $\overrightarrow{\mathrm{AC}}$ được gọi là tổng của hai vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{BC}}$, kí hiệu là $\overrightarrow{\mathrm{AC}}$ = $\overrightarrow{\mathrm{AB}}$ + $\overrightarrow{\mathrm{BC}}$.

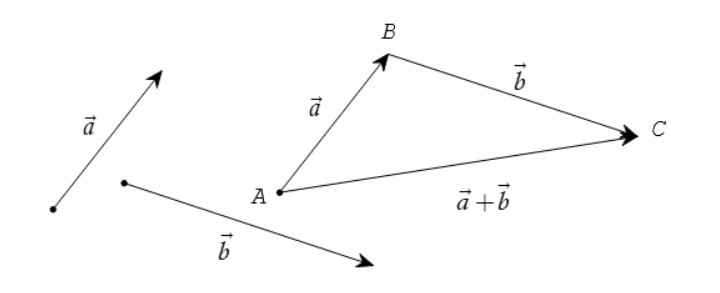
Phép lấy tổng của hai vectơ còn được gọi là phép cộng vectơ.

9.2. Quy tắc hình bình hành

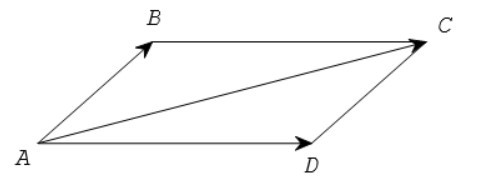
Nếu ABCD là hình bình hành thì $\overrightarrow{\mathrm{AB}}$+$\overrightarrow{\mathrm{AD}}$= $\overrightarrow{\mathrm{AC}}$.

9.3. Tính chất

Với ba vectơ tùy ý $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$, $\overrightarrow{\mathrm{c}}$ ta có:

$\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$ = $\overrightarrow{\mathrm{b}}$ + $\overrightarrow{\mathrm{a}}$ (tính chất giao hoán) ;

($\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$) + $\overrightarrow{\mathrm{c}}$ = $\overrightarrow{\mathrm{a}}$ + ($\overrightarrow{\mathrm{b}}$ + $\overrightarrow{\mathrm{c}}$) (tính chất kết hợp);

$\overrightarrow{\mathrm{a}}$ + $\overrightarrow{0}$ = $\overrightarrow{0}$ + $\overrightarrow{\mathrm{a}}$ = $\overrightarrow{\mathrm{a}}$ (tính chất của vectơ–không).

Chú ý: Tổng ba vectơ $\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$ + $\overrightarrow{\mathrm{c}}$ được xác định theo một trong hai cách sau:

($\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$) + $\overrightarrow{\mathrm{c}}$ hoặc $\overrightarrow{\mathrm{a}}$ + ($\overrightarrow{\mathrm{b}}$ + $\overrightarrow{\mathrm{c}}$).

10. Hiệu của hai vectơ

10.1. Hai vectơ đối nhau

Định nghĩa: Vectơ có cùng độ dài và ngược hướng với vectơ $\overrightarrow{\mathrm{a}}$ được gọi là vectơ đối của vectơ $\overrightarrow{\mathrm{a}}$, kí hiệu là –$\overrightarrow{\mathrm{a}}$. Hai vectơ $\overrightarrow{\mathrm{a}}$ và –$\overrightarrow{\mathrm{a}}$ được gọi là hai vectơ đối nhau.

Quy ước: Vectơ đối của vectơ $\overrightarrow{0}$ là vectơ $\overrightarrow{0}$.

Nhận xét:

+) $\overrightarrow{\mathrm{a}}$ + (–$\overrightarrow{\mathrm{a}}$) = (–$\overrightarrow{\mathrm{a}}$) + $\overrightarrow{\mathrm{a}}$ = $\overrightarrow{0}$

+) Hai vectơ $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$ là hai vectơ đối nhau khi và chỉ khi $\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$ = $\overrightarrow{0}$.

+) Với hai điểm A, B, ta có: $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BA}}=\overrightarrow{0}$.

Lưu ý: Cho hai điểm A, B. Khi đó hai vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{BA}}$ là hai vectơ đối nhau, tức là $\overrightarrow{\mathrm{BA}}=-\overrightarrow{\mathrm{AB}}.$  

Chú ý:

– I là trung điểm của đoạn thẳng AB khi và chỉ khi $\overrightarrow{\mathrm{IA}}+\overrightarrow{\mathrm{IB}}=\overrightarrow{0}$.

– G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}=\overrightarrow{0}$.

10.2. Hiệu của hai vectơ

Hiệu của hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$, kí hiệu là $\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$, là tổng của vectơ $\overrightarrow{\mathrm{a}}$và vectơ đối của vectơ $\overrightarrow{\mathrm{b}}$, tức là $\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$ = $\overrightarrow{\mathrm{a}}$ + (–$\overrightarrow{\mathrm{b}}$).

Phép lấy hiệu của hai vectơ được gọi là phép trừ hai vectơ.

Nhận xét: Với ba điểm bất kì A, B, O ta có: $\overrightarrow{\mathrm{AB}}$ = $\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}$.

11. Tích của vectơ với một số

Cho một số k ≠ 0 và vectơ $\overrightarrow{\mathrm{a}}$ ≠ $\overrightarrow{0}$. Tích của một số k với vectơ $\overrightarrow{\mathrm{a}}$ là một vectơ, kí hiệu là k$\overrightarrow{\mathrm{a}}$, được xác định như sau:

+ cùng hướng với $\overrightarrow{\mathrm{a}}$ nếu k > 0, ngược hướng với $\overrightarrow{\mathrm{a}}$ nếu k < 0;

+ có độ dài bằng $\left|\mathrm{k}\right|$.$\left|\overrightarrow{\mathrm{a}}\right|$

Quy ước: 0$\overrightarrow{\mathrm{a}}$ = $\overrightarrow{0}$, k$\overrightarrow{0}$ = $\overrightarrow{0}$

Phép lấy tích của một số với một vectơ gọi là phép nhân một số với một vectơ.

Tính chất

Với hai vectơ bất kì $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$ và hai số thực h, k, ta có:

+) k($\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$) = k$\overrightarrow{\mathrm{a}}$ + k$\overrightarrow{\mathrm{b}}$; k($\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$) = k$\overrightarrow{\mathrm{a}}$ – k$\overrightarrow{\mathrm{b}}$;

+) (h + k)$\overrightarrow{\mathrm{a}}$ = h$\overrightarrow{\mathrm{a}}$ + k$\overrightarrow{\mathrm{a}}$;

+) h(k$\overrightarrow{\mathrm{a}}$) = (hk)$\overrightarrow{\mathrm{a}}$;

+) 1$\overrightarrow{\mathrm{a}}$ = $\overrightarrow{\mathrm{a}}$; (–1)$\overrightarrow{\mathrm{a}}$ = –$\overrightarrow{\mathrm{a}}$.

Nhận xét: k$\overrightarrow{\mathrm{a}}$ = $\overrightarrow{0}$ khi và chỉ khi k = 0 hoặc $\overrightarrow{\mathrm{a}}$ = $\overrightarrow{0}$.

– Nếu I là trung điểm của đoạn thẳng AB thì $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}=2\overrightarrow{\mathrm{MI}}$ với điểm M bất kì.

– Nếu G là trọng tâm của tam giác ABC thì $\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}+\overrightarrow{\mathrm{MC}}=3\overrightarrow{\mathrm{MG}}$ với điểm M bất kì.

– Điều kiện cần và đủ để hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ ($\overrightarrow{\mathrm{b}}$ ≠ 0) cùng phương là có một số thực k để $\overrightarrow{\mathrm{a}}$ = k$\overrightarrow{\mathrm{b}}$.

– Điều kiện cần và đủ để ba điểm phân biệt A, B, C thẳng hàng là có số thực k để $\overrightarrow{\mathrm{AB}}=\mathrm{k}\overrightarrow{\mathrm{AC}}$.

Nhận xét: Trong mặt phẳng, cho hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ không cùng phương. Với mỗi vectơ $\overrightarrow{\mathrm{c}}$ có duy nhất cặp số (x; y) thoả mãn $\overrightarrow{\mathrm{c}}=\mathrm{x}\overrightarrow{\mathrm{a}}+\mathrm{y}\overrightarrow{\mathrm{b}}$.

12. Tích vô hướng của hai vectơ

12.1. Tích vô hướng của hai vectơ có chung điểm đầu

– Góc giữa hai vectơ $\overrightarrow{\mathrm{OA}}$, $\overrightarrow{\mathrm{OB}}$ là góc giữa hai tia OA, OB và được kí hiệu là $\left(\overrightarrow{\mathrm{OA}},\overrightarrow{\mathrm{OB}}\right)$

– Tích vô hướng của hai vectơ $\overrightarrow{\mathrm{OA}}$ và $\overrightarrow{\mathrm{OB}}$ là một số thực, kí hiệu là $\overrightarrow{\mathrm{OA}}$.$\overrightarrow{\mathrm{OB}}$, được xác định bởi công thức: $\overrightarrow{\mathrm{OA}}.\overrightarrow{\mathrm{OB}}=\left|\overrightarrow{\mathrm{OA}}\right|.\left|\overrightarrow{\mathrm{OB}}\right|.\cos \left(\overrightarrow{\mathrm{OA}},\overrightarrow{\mathrm{OB}}\right)$.

12.2. Tích vô hướng của hai vectơ tùy ý

Định nghĩa:

Cho hai vectơ $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$ khác $\overrightarrow{0}.$ Lấy một điểm O và vẽ vectơ $\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{a}},\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{b}}$ (Hình vẽ).

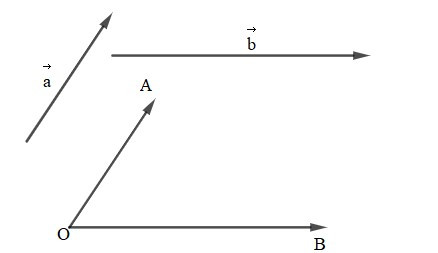
+ Góc giữa hai vectơ $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$, kí hiệu $\left(\overrightarrow{\mathrm{a}},\overrightarrow{\mathrm{b}}\right)$, là góc giữa hai vectơ $\overrightarrow{\mathrm{OA}}$, $\overrightarrow{\mathrm{OB}}$.

+ Tích vô hướng của hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$, kí hiệu $\overrightarrow{\mathrm{a}}$.$\overrightarrow{\mathrm{b}}$ là tích vô hướng của hai vectơ $\overrightarrow{\mathrm{OA}}$ và $\overrightarrow{\mathrm{OB}}$. Như vậy, tích vô hướng của hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ là một số thực được xác định bởi công thức: $\overrightarrow{\mathrm{a}}$.$\overrightarrow{\mathrm{b}}$ = $\left|\overrightarrow{\mathrm{a}}\right|.\left|\overrightarrow{\mathrm{b}}\right|.\cos \left(\overrightarrow{\mathrm{a}},\overrightarrow{\mathrm{b}}\right)$.

Quy ước: Tích vô hướng của một vectơ bất kì với vectơ $\overrightarrow{0}$ là số 0.

Chú ý:

+) $\left(\overrightarrow{\mathrm{a}},\overrightarrow{\mathrm{b}}\right)$ = $\left(\overrightarrow{\mathrm{b}},\overrightarrow{\mathrm{a}}\right)$

+) Nếu $\left(\overrightarrow{\mathrm{a}},\overrightarrow{\mathrm{b}}\right)$ = 90° thì ta nói hai vectơ $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$ vuông góc với nhau, kí hiệu $\overrightarrow{\mathrm{a}}$ ⊥ $\overrightarrow{\mathrm{b}}$ hoặc $\overrightarrow{\mathrm{a}}$ ⊥ $\overrightarrow{\mathrm{b}}$. Khi đó $\left|\overrightarrow{\mathrm{a}}\right|$.$\overrightarrow{\mathrm{b}}$ = $\left|\overrightarrow{\mathrm{a}}\right|.\left|\overrightarrow{\mathrm{b}}\right|.\cos 90°$= 0.

+) Tích vô hướng của hai vectơ cùng hướng bằng tích hai độ dài của chúng.

+) Tích vô hướng của hai vectơ ngược hướng bằng số đối của tích hai độ dài của chúng.

12.3. Tính chất

Với hai vectơ bất kì $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$ và số thực k tùy ý, ta có:

+) $\overrightarrow{\mathrm{a}}$.$\overrightarrow{\mathrm{b}}$ = $\overrightarrow{\mathrm{b}}$.$\overrightarrow{\mathrm{a}}$ (tính chất giao hoán);

+) $\overrightarrow{\mathrm{a}}.\left(\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{c}}\right)=\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{c}}$ (tính chất phân phối);

+) $\left(\mathrm{k}\overrightarrow{\mathrm{a}}\right)\overrightarrow{\mathrm{b}}=\mathrm{k}\left(\overrightarrow{\mathrm{a}}.\overrightarrow{\mathrm{b}}\right)=\overrightarrow{\mathrm{a}}.\left(\mathrm{k}\overrightarrow{\mathrm{b}}\right)$;

+) ${\overrightarrow{\mathrm{a}}}^2$ ≥ 0, ${\overrightarrow{\mathrm{a}}}^2$ = 0 ⟺ $\overrightarrow{\mathrm{a}}$ = $\overrightarrow{0}$.

Trong đó, kí hiệu $\overrightarrow{\mathrm{a}}$.$\overrightarrow{\mathrm{a}}$ = ${\overrightarrow{\mathrm{a}}}^2$ và biểu thức này được gọi là bình phương vô hướng của vectơ $\overrightarrow{\mathrm{a}}$.

Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:

Bài 6: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây

Bài 2: Hoán vị. Chỉnh hợp

Bài 3: Tổ hợp