Với giải Hoạt động 1 trang 83 SGK Toán lớp 10 Cánh diều chi tiết trong Bài 4: Tổng và hiệu của hai vectơ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SGK Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 4: Tổng và hiệu của hai vectơ

Hoạt động 1 trang 83 Toán lớp 10: Một vật dịch chuyển từ A đến B và tiếp tục dịch chuyển từ B đến C (Hình 49).

a) Biểu diễn vectơ dịch chuyển của vật từ A đến B và từ B đến C.

b) Xác định vectơ dịch chuyển tổng hợp của vật.

Lời giải:

a) Vật dịch chuyển từ A đến B theo vectơ $\overrightarrow{AB}$, vật dịch chuyển từ B đến C theo vectơ $\overrightarrow{BC}$.

b) Vật di chuyển từ A đến B và từ B đến C, nghĩa là điểm đầu đường đi của vật là A và điểm cuối đường đi là C, do đó vectơ dịch chuyển tổng hợp của vật là vectơ $\overrightarrow{AC}$ .

Lý thuyết Tổng của hai vectơ

1.1. Định nghĩa

– Với ba điểm bất kì A, B, C, vectơ $\overrightarrow{\mathrm{AC}}$ được gọi là tổng của hai vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{BC}}$, kí hiệu là $\overrightarrow{\mathrm{AC}}$ = $\overrightarrow{\mathrm{AB}}$ + $\overrightarrow{\mathrm{BC}}$.

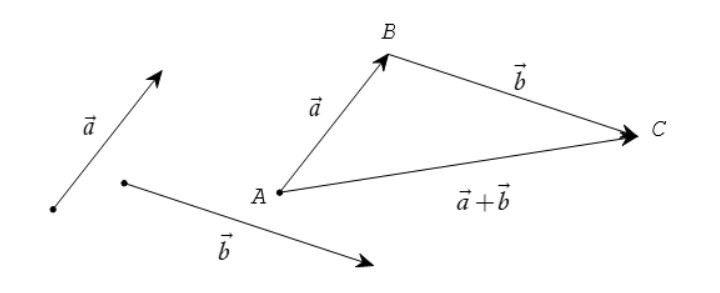
– Cho hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$. Lấy một điểm A tùy ý, vẽ $\overrightarrow{\mathrm{AB}}$= $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{BC}}$= $\overrightarrow{\mathrm{b}}$. Vectơ $\overrightarrow{\mathrm{AB}}$ được gọi là tổng của hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$. Ta kí hiệu tổng của hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ là $\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$. Vậy $\overrightarrow{\mathrm{AC}}$ = $\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$.

Phép lấy tổng của hai vectơ còn được gọi là phép cộng vectơ.

Ví dụ: Cho hình chữ nhật ABCD tâm O. Tính:

a) $\overrightarrow{\mathrm{OA}}$+ $\overrightarrow{\mathrm{DC}}$

b) $\overrightarrow{\mathrm{BC}}$ + $\overrightarrow{\mathrm{OA}}$

Hướng dẫn giải:

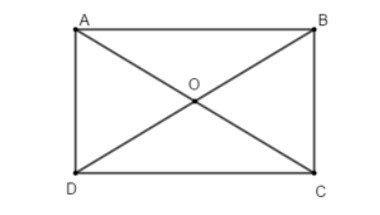
a) Vì ABCD là hình chữ nhật nên AB // CD và AB = CD.

⇒ $\overrightarrow{\mathrm{DC}}$ = $\overrightarrow{\mathrm{AB}}$.

⇒ $\overrightarrow{\mathrm{OA}}$+ $\overrightarrow{\mathrm{DC}}$ = $\overrightarrow{\mathrm{OA}}$+ $\overrightarrow{\mathrm{AB}}$= $\overrightarrow{\mathrm{OB}}$.

b) Vì A, O, C thẳng hàng (O là trung điểm của đường chéo AC)

⇒ $\overrightarrow{\mathrm{OA}}$= $\overrightarrow{\mathrm{CO}}$.

⇒ $\overrightarrow{\mathrm{BC}}$ + $\overrightarrow{\mathrm{OA}}$= $\overrightarrow{\mathrm{BC}}$ + $\overrightarrow{\mathrm{CO}}$ = $\overrightarrow{\mathrm{BO}}$.

1.2. Quy tắc hình bình hành

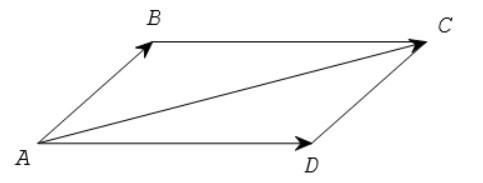
Nếu ABCD là hình bình hành thì $\overrightarrow{\mathrm{AB}}$+$\overrightarrow{\mathrm{AD}}$= $\overrightarrow{\mathrm{AC}}$.

Ví dụ: Chứng minh quy tắc hình bình hành.

Hướng dẫn giải:

Ta có: $\overrightarrow{\mathrm{AD}}$= $\overrightarrow{\mathrm{BC}}$.

Suy ra: $\overrightarrow{\mathrm{AB}}$+$\overrightarrow{\mathrm{AD}}$= $\overrightarrow{\mathrm{AB}}$+ $\overrightarrow{\mathrm{BC}}$= $\overrightarrow{\mathrm{AC}}$.

1.3. Tính chất

Với ba vectơ tùy ý $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$, $\overrightarrow{\mathrm{c}}$ ta có:

$\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$ = $\overrightarrow{\mathrm{b}}$ + $\overrightarrow{\mathrm{a}}$ (tính chất giao hoán) ;

($\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$) + $\overrightarrow{\mathrm{c}}$ = $\overrightarrow{\mathrm{a}}$ + ($\overrightarrow{\mathrm{b}}$ + $\overrightarrow{\mathrm{c}}$) (tính chất kết hợp);

$\overrightarrow{\mathrm{a}}$ + $\overrightarrow{0}$ = $\overrightarrow{0}$ + $\overrightarrow{\mathrm{a}}$ = $\overrightarrow{\mathrm{a}}$ (tính chất của vectơ–không).

Chú ý: Tổng ba vectơ $\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$ + $\overrightarrow{\mathrm{c}}$ được xác định theo một trong hai cách sau:

($\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$) + $\overrightarrow{\mathrm{c}}$ hoặc $\overrightarrow{\mathrm{a}}$ + ($\overrightarrow{\mathrm{b}}$ + $\overrightarrow{\mathrm{c}}$).

Ví dụ: Cho 5 điểm tùy ý A, B, C, D, E. Chứng minh rằng:

a) $\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{EC}}+\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{BE}}$ = $\overrightarrow{\mathrm{BA}}$.

b) $\overrightarrow{\mathrm{AB}}$+ $\overrightarrow{\mathrm{CD}}$+ $\overrightarrow{\mathrm{EA}}$= $\overrightarrow{\mathrm{CB}}$ + $\overrightarrow{\mathrm{ED}}$.

Hướng dẫn giải:

a) Ta có:

$\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{EC}}+\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{BE}}$ 

= $\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{BE}}+\overrightarrow{\mathrm{EC}}$              (áp dụng tính chất giao hoán)

= $\left(\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{DA}}\right)+\left(\overrightarrow{\mathrm{BE}}+\overrightarrow{\mathrm{EC}}\right)$        (áp dụng tính chất kết hợp)

= $\overrightarrow{\mathrm{CA}}+\overrightarrow{\mathrm{BC}}$  (áp dụng quy tắc cộng vectơ)

= $\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}$  (áp dụng tính chất giao hoán)

= $\overrightarrow{\mathrm{BA}}$ (áp dụng quy tắc cộng vectơ) (đpcm).

Vậy $\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{EC}}+\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{BE}}$ = $\overrightarrow{\mathrm{BA}}$.

b) Ta có:

$\overrightarrow{\mathrm{AB}}$+ $\overrightarrow{\mathrm{CD}}$+ $\overrightarrow{\mathrm{EA}}$

= $\left(\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CB}}\right)+\overrightarrow{\mathrm{CD}}+\left(\overrightarrow{\mathrm{ED}}+\overrightarrow{\mathrm{DA}}\right)$         (áp dụng quy tắc cộng vectơ)

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}+\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{DA}}$               (áp dụng tính chất giao hoán)

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}+\left(\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CD}}\right)+\overrightarrow{\mathrm{DA}}$  (áp dụng tính chất kết hợp)

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}+\stackrel{\rightharpoonup }{\mathrm{AD}}+\overrightarrow{\mathrm{DA}}$             (áp dụng quy tắc cộng vectơ)

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}+\left(\stackrel{\rightharpoonup }{\mathrm{AD}}+\overrightarrow{\mathrm{DA}}\right)$           (áp dụng tính chất kết hợp)

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}+\overrightarrow{\mathrm{AA}}$ 

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}+\overrightarrow{0}$      (vectơ có điểm đầu và điểm cuối trùng nhau là vectơ–không)

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}$            (áp dụng tính chất vectơ–không) (đpcm).