Với Công thức tính thế năng Vật lí lớp 10 chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ các công thức tính suất điện động từ đó biết cách làm bài tập Vật lí 10. Mời các bạn đón xem:

Công thức tính thế năng 2024 mới nhất 

1. Khái niệm thế năng

- Thế năng tồn tại dưới dạng năng lượng dự trữ khi vật ở một độ cao so với mốc thế năng hay vật bị biến dạng và đều có khả năng sinh công.

- Có hai dạng thế năng:

+ Thế năng trọng trường (thế năng hấp dẫn): phụ thuộc vị trí tương đối của vật so với mặt đất.

Em bé ngồi trên cầu trượt, em bé có thế năng trọng trường

+ Thế năng đàn hồi: phụ thuộc độ biến dạng của vật so với trạng thái chưa biến dạng.

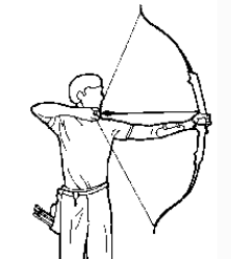
Thế năng đàn hồi dự trữ trong dây cung khi bị kéo căng

2. Công thức thế năng

- Khi một vật có khối lượng m đặt ở độ cao z so với mặt đất (trong trọng trường của Trái Đất) thì thế năng trọng trường của vật được định nghĩa bằng công thức:

W_t = mgz

Trong đó:  m: khối lượng của vật (kg)

g: gia tốc trọng trường (m/s²).

z: Độ cao của vật so với gốc thế năng (m)

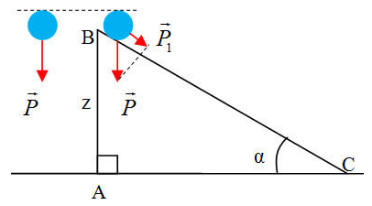
+ Thế năng ở ngay trên mặt đất bằng 0 (vì z = 0). Vì vậy, mặt đất được chọn là mốc (hay gốc) thế năng.

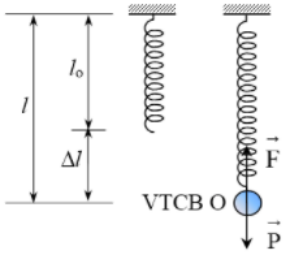
- Thế năng đàn hồi của một lò xo ở trạng thái có biến dạng Dℓ là:

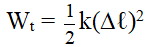
     Trong đó k: Độ cứng của lò xo (N/m)

Dℓ: Độ biến dạng của lò xo(m).

W_t: Thế năng đàn hồi (J).

3. Kiến thức mở rộng

- Từ công thức thế năng trọng trường, ta có thể tính:

+ Khối lượng của vật: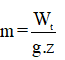 

+ Độ cao của vật so với gốc thế năng: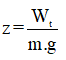 

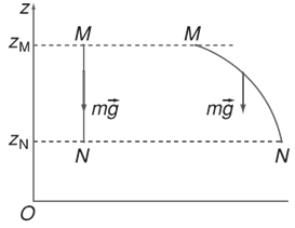
- Liên hệ giữa biến thiên thế năng và công của trọng lực:

      Khi một vật chuyển động trong trọng trường từ vị trí M đến vị trí N thì công của trọng lực của vật có giá trị bằng hiệu thế năng trọng trường tại M và tại N.

A_MN= W_t1 – W_t2= ∆W_t = mgz_M - mgz_N

   Trong đó: A₁₂: công của trọng lực chuyển từ vị trí 1 sang vị trí 2

W_t1 – W_t2= : độ giảm thế năng

Chú ý: Nếu A_MN > 0 thì  ∆W_t > 0: thế năng của vật giảm 

     Nếu A₁₂ < 0 thì  ∆W_t < 0: thế năng của vật tăng

- Từ công thức thế năng đàn hồi, ta có thể tính:

+ Độ cứng của lò xo: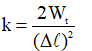 

+ Độ biến dạng của lò xo: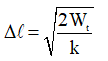 

- Công của lực đàn hồi thực hiện khi lò xo biến dạng và đầu lò xo có gắn quả nặng di chuyển từ vị trí x₁ đến vị trí x₂bằng độ giảm thế năng đàn hồi:

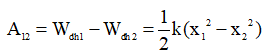
Trong đó: W_đh1 là thế năng đàn hồi của lò xo tại vị trí x₁ (J)

       W_đh2 là thế năng đàn hồi của lò xo tại vị trí x₂ (J)

        A₁₂ là công của lực đàn hồi (J)

=> Công của lực đàn hồi chỉ phụ thuộc các vị trí đầu và cuối của biến dạng. Lực đàn hồi cũng là lực thế.

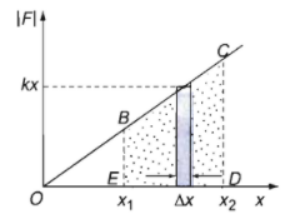
Đồ thị để tính công của lực đàn hồi

4. Bài tập thế năng

Bài 1: Hai vật có khối lượng là m và 2m đặt ở hai độ cao lần lượt là 2h và h. Tỉ số giữa thế năng trọng trường của vật thứ nhất so với vật thứ hai là?

Lời giải

Thế năng của vật 1 có giá trị là: W_t1 = m.g.2.h = 2mgh

Thế năng của vật 2 có giá trị là: W_t2 = m.g.2.h = 2mgh

=> Tỉ số giữa thế năng trọng trường của vật thứ nhất so với vật thứ hai là:

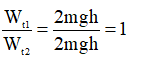
Bài 2: Một người kéo một lực kế, số chỉ của lực kế là 400N, độ cứng của lò xo lực kế là 1000N/m. Công do người thực hiện bằng bao nhiêu?

Lời giải

 Lực đàn hồi cũng chính là số chỉ của lực kế: F = |k∆l| = 400N

=> Độ biến dạng của lò xo so với vị trí ban đầu: 

Chọn mốc thế năng tại vị trí ban đầu (lò xo không dãn – không nén)

=> Công do người thực hiện chính bằng thế năng đàn hồi của lò xo:

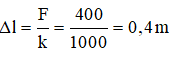
Bài 3: Một xe có khối lượng m = 2,8 kg chuyển động theo quỹ đạo cong như hình vẽ. Độ cao của các điểm A, B, C, D, E được tính đối với mặt đất và có các giá trị: h_A = 6 m, h_B = 3 m, h_C = 4 m, h_D = 1,5 m, h_E = 7 m. Lấy g = 10 m/s².

Tính độ biến thiên thế năng của xe trong trọng lượng khi nó di chuyển:

a. Từ A đến B.

b. Từ B đến C.

c. Từ A đến D.

d. Từ A đến E.

Lời giải

a. Từ A đến B:

ΔW_t = m.g.(h_B- h_A ) = 2,8.10.(3-6)= -84J

b. Từ B đến C:

ΔW_t = m.g.(h_C - h_B ) = 2,8.10.(4-3)= 28J

c. Từ A đến D:

ΔW_t = m.g.(h_D - h_A ) = 2,8.10.(1,5-6)= -126J ⇒ thế năng giảm.

d. Từ A đến E:

ΔW_t = m.g.(h_E - h_A ) = 2,8.10.(7-6) = 28J

Bài 4: Một vật có khối lượng 3 kg được đặt ở vị trí trong trọng trường và có thế năng tại đó W_t1 = 500 J. Thả vật rơi tự do đến mặt đất có thế năng W_t2 = -900 J.

a. Hỏi vật đã rơi từ độ cao nào so với mặt đất.

b. Xác định vị trí ứng với mức không của thế năng đã chọn.

c. Tìm vận tốc của vật khi vật qua vị trí này.

Lời giải

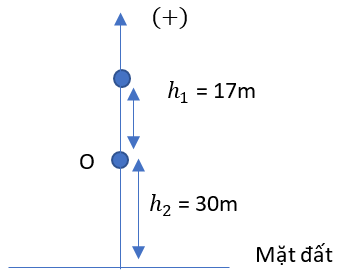
Theo đề bài có thế năng tại mặt đất là -900J => Mặt đất không được chọn làm mốc thế năng

Giả sử mốc thế năng được chọn tại vị trí O cách mặt đất độ cao là h₂ (m)

Chọn chiều dương hướng lên trên.

a. Ta có: W_t2 = m.g.h₂ => h₂ = 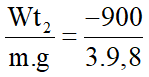 = -30(m)

=> Mặt đất thấp hơn mốc thế năng 30m theo chiều âm.

Tại vị trí có W_t1 = 500J ở độ cao so với mốc thế năng là

W_t1 = m.g.h₁ => h₁ = 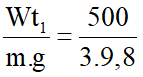 ≈ 17(m)

=> Tổng độ cao của vật so với mặt đất là h = h₁ + h₂ = 30 + 17 = 47(m)

b. Vị trí ứng với mốc thế năng chọn là 17(m)

c. Vận tốc tại vị trí chọn mốc thế năng

Ta có: v² - v₀² = 2.g.h₁ => v =  = 18,25m/s

Bài 5: Một vật có khối lượng m = 6 kg được đặt ở một vị trí trong trọng trường và có thế năng tại vị trí đó bằng W_t1 = 720 J. Thả tự do cho vật rơi tới mặt đất, tại đó thế năng của vật bằng W_t2 = - 240 J. Lấy g = 10 m/s².

a. Hỏi vật đã rơi từ độ cao nào so với mặt đất?

b. Hãy xác định gốc thế năng đã được chọn ở đâu.

c. Tìm vận tốc vật khi đi qua vị trí gốc thế năng.

Lời giải

Theo đề bài có thế năng tại mặt đất là -240J => Mặt đất không được chọn làm mốc thế năng

Giả sử mốc thế năng được chọn tại vị trí O cách mặt đất độ cao là h₂ (m)

Chọn chiều dương hướng lên trên.

a. Ta có:

W_t2 = m.g.h₂ => h₂ = 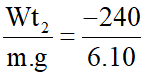 = -4(m)

=> Mặt đất thấp hơn mốc thế năng 4m theo chiều âm.

Tại vị trí có W_t1 = 720J ở độ cao so với mốc thế năng là

W_t1 = m.g.h₁ => h₁ = 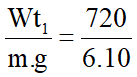 ≈ 12(m)

=> Tổng độ cao của vật so với mặt đất là h = h₁ + h₂ = 4 + 12 = 16(m)

b. Vị trí ứng với mốc thế năng chọn là 12(m)

c. Vận tốc tại vị trí chọn mốc thế năng

Ta có: v² - v₀² = 2.g.h₁ => v = 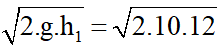 ≈ 15,5 m/s

Bài 6: Một cần cẩu nâng một thùng hàng có khối lượng 420 kg từ mặt đất lên độ cao 3 m ( tính theo di chuyển khối tâm của thùng), sau đó đổi hương và hạ thùng này xuống sàn một ôtô tải ở độ cao 1,25 m so với mặt đất.

a. Tìm thế năng của thùng trong trọng trương khi ở độ cao 3 m. Tính công của lực phát động ( lực căng của dây cáp) để nâng thùng hàng lên độ cao này.

b. Tìm độ biến thiên thế năng khi hạ thùng từ độ cao 3 m xuống sàn ôtô. Công của trọng lực có phụ thuộc cách di chuyển thùng giữa hai vị trí đó hay không? Tại sao?

Lời giải

a. Thế năng của thùng: W_t = mgz = 420.10.3 = 12600 (J).

Coi thùng được nâng đều, lực phát động có độ lớn bằng trọng lực. Độ giảm thế năng bằng công của trọng lực:

W_t - 0 = - A_P.

Công của lực phát động: A_F = - A_P = W_t = 12600 (J).

b. Độ biến thiên thế năng khi hạ thùng xuống sàn ôtô:

W = W₂ - W₁ = mg(h₂ - h₁ ) = 420.10.(1,25-3) = -7350 (J)

Trong trường hợp này thế năng giảm.

Công của trọng lực không phụ thuộc vào cách di chuyển thùng giữa hai vị trí vì trọng lực là lực thế, công của nó chỉ phụ thuộc vào mực chênh lệch độ cao giữa hai vị trí đầu và cuối mà không phụ thuộc vào dạng đường đi.

Bài 7: Một người đứng yên trên cầu ném một hòn đá có khối lượng 50 g lên cao theo phương thẳng đứng. Hòn đá lên đến độ cao 6 m (tính từ điểm ném) thì dừng và rơi trở xuống mặt nước thấp hơn điểm ném 2 m.

1) Tìm thế năng của vật trong trọng trường ở vị trí cao nhất nếu chọn:

a. Điểm ném vật làm mốc.

b. Mặt nước làm mốc.

2) Tính công do trọng lực thực hiện khi hòn đá đi từ điểm ném lên đến điểm cao nhất và khi nó rơi từ điểm cao nhất tới mặt nước. Công này có phụ thuộc vào việc chọn hai mốc khác nhau ở câu 1 hay không?

Lời giải

1) Chọn trục tọa độ Oy hướng thẳng đứng từ dưới lên.

a. Điểm ném làm mốc, vị trí cao nhất có tọa độ h = 6 m.

⇒ W_t = mgh = 2,94 (J).

b. Mặt nước làm mốc, vị trí cao nhất có tọa độ:

h’ = h + 2 = 6 + 2 = 8 m.

W_t' = mgh’ = 3,92 (J).

2)

- Công do trọng lực thực hiện khi vật chuyển động từ điểm ném đến vị trí cao nhất:

   + Điểm ném làm mốc: A₁₂ = W_t1 - W_t2 = 0 - 2,94 = -2,94 (J).

   + Mặt nước làm mốc: A₁₂ = W '_t1 - W '_t = (0 + 0,98)- 3,92 = - 2,94 (J).

Ta nhận thấy công của trọng lực không phụ thuộc vào việc chọn gốc toạn độ mà chỉ phụ thuộc mức chênh lệch giữa hai độ cao. Dấu trừ chứng tỏ trọng lực thực hiện công âm khi vật di chuyển từ thấp lên cao.

- Công do trọng lực thực hiện khi vật rơi từ điểm cao nhất tới mặt nước:

   + Điểm ném làm mốc: A₂₃ = W_t2 - W_t3 = 2,94 - (0-0,98) = 3,92 (J).

   + Mặt nước làm mốc: A₂₃ = W '_t2- W '_t3 = 3,92 - 0 = 3,92 (J).