Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Con lắc đơn là gì? Công thức tính chu kì, tần số góc của dao động và bài tập, tài liệu bao gồm có định nghĩa, công thức tính và các dạng bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Vật lí sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Con lắc đơn là gì? Công thức tính chu kì, tần số góc của dao động và bài tập
1. Khái niệm về con lắc đơn
Con lắc đơn là một hệ bao gồm một vật nhỏ có khối lượng m, được treo ở đầu một sợi dây không dãn, khối lượng của nó nhỏ không đáng kể, chiều dài là l, đầu trên của sợi dây được treo vào một điểm cố định.
2. Vị trí cân bằng của con lắc đơn
Vị trí cân bằng của con lắc đơn chính là vị trí dây treo có phương thẳng đứng. Hoặc khi kéo nhẹ quả cầu cho dây treo lệch ra khỏi vị trí cân bằng một góc rồi thả tay ra, ta thấy sự dao động của con lắc quanh vị trí cân bằng trong mặt phẳng đứng đi qua điểm treo và vị trí ban đầu của vật. Từ đó ta hãy xem dao động của con lắc đơn đó có phải là dao động điều hòa hay không.
3. Phương trình dao động của con lắc đơn
Điều kiện để con lắc đơn dao động điều hòa là góc lệch cực đại của dây treo:
α0 < hoặc = 10º
- Phương trình dao động của con lắc: s =s0.cos(ωt +φ)
- Phương trình dao động theo li độ góc: α = α0.cos(ωt +φ)
4. Phương trình vận tốc và gia tốc
- Phương trình vận tốc của dao động: v = s' = ω . So . sin(ω . t + φ + π/2)
=> vmax = ω. So khi vật qua vị trí cân bằng.
(v/vmax)^2 + (s/So)2 = 1 hoặc (v/vmax)^2 + ( α/ αo)^2 = 1
- Phương trình gia tốc
Trong quá trình chuyển động của con lắc, nó chịu 2 gia tốc là: gia tốc hướng tâm và gia tốc tiếp tuyến.
Phương trình gia tốc tiếp tuyến là: att = v' = -ω ^ 2.So.cos(ω.t + phi) = - ω^2. s
Phương trình gia tốc hướng tâm: aht = v^2/ l
Vậy ta có gia tốc tổng hợp là:
ath = căn (aht2 + att2)
Nhận xét: Trong quá trình dao động, gia tốc nhỏ nhất của con lắc luôn lớn hơn 0.
5. Công thức tính chu kỳ và tần số
Chu kỳ: (Đơn vị tính: s)
Tần số: (Đơn vị tính: Hz)
6. Công thức tính năng lượng của con lắc đơn
Các công thức tính năng lượng của con lắc đơn dao động điều hòa là:
Lưu ý:
7. Công thức tính vận tốc và lực căng dây
Khi vật ở vị trí có li độ góc alpha, các lực tác dụng lên vật gồm: trọng lực P = mg và lực căng T của sợi dây. Hợp của hai lực này chính là lực hướng tâm, vật chuyển động trên quỹ đạo tròn có bán kính R = 1. Ta có:
P + T = Fht
v = căn 2gl(cos alpha - cos alphao) => vmax = căn 2gl.(1 - cos alphao)
Công thức tính lực căng dây của con lắc đơn
T = mg.(3.cos alpha - 2.cos alphao)
=> Tmax = mg(3 - 2.cos alphao). (Khi vật đi ngang qua vị trí cân bằng)
=> Tmin = mg.cos alphao (Khi vật ở vị trí biên)
8. Ứng dụng: Xác định gia tốc rơi tự do
Trong lĩnh vực địa chất, các nhà địa chất quan tâm đến những tính chất đặc biệt của lớp bề mặt Trái Đất và thường xuyên phải đo gia tốc trọng trường ở một nơi nào đó. Sau đây là một ví dụ.
Dùng một con lắc có chiều dài l tính đến tâm của quả cầu. Đo thời gian của một số dao động toàn phần, từ đó suy ra chu kì T. Sau đó ta tính g ttheo công thức g = 4pi2.l/T2. Lặp lại thí nghiệm nhiều lần, mỗi lần rút ngắn chiều dài con lắc đi một đoạn. Lấy giá trị trung bình g ở các lần đo, ta được gia tốc rơi tự do tại nơi đó.
9. Bài tập vận dụng
Bài tập 1: Tại cùng một nơi trên mặt đất, một con lắc có chiều dài lần lượt là l+10(cm), l(cm) và l-10(cm) thì con lắc dao động điều hòa với chu kì lần lượt là 3, và T. Giá trị của T là
A. T = 7,48 s. B. T = 1,63 s. C.T = 2,00 s. D. T =2,65 s.
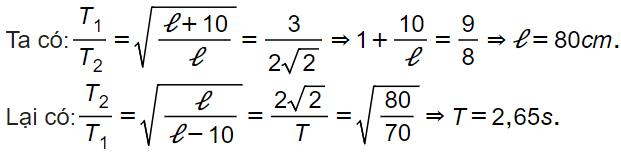
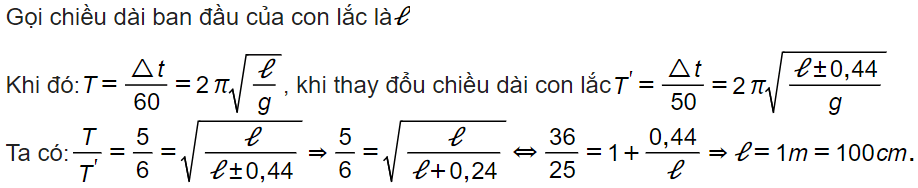
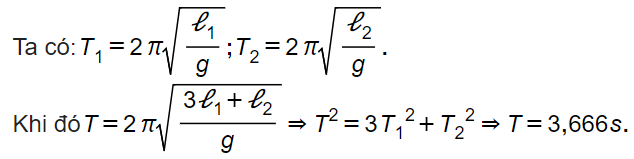
A. 148 cm. B. 133 cm. C. 108 cm. D. 97,2 cm.
Lời giải chi tiết
![]()
Chọn D.
Bài tập 5: [Trích đề thi đại học năm 2013]. Một con lắc đơn có chiều dài 121 cm dao động điều hòa tại nơi có gia tốc trọng trường g. Lấy . Chu kì dao động của con lắc là
A. 0,5 s. B. 2 s. C. 1 s. D. 2,2 s.
Lời giải chi tiết
![]()
Chọn D.
Bài tập 6: [Trích đề thi đại học năm 2009]. Tại nơi có gia tốc trọng trường g = 9,8 m/s, một con lắc đơn và một con lắc lò xo nằm ngang dao động điều hòa với cùng tần số. Biết con lắc đơn có chiều dài 49 cm và lò xo có độ cứng 10 N/m. Khối lượng vật nhỏ của con lắc lò xo là
A. 0,125 kg. B. 0,500 kg. C. 0,750 kg. D. 0,250 kg.
Lời giải chi tiết
![]()
Chọn B.
Bài tập 7: Một con lắc đơn có chiều dài dao động điều hòa tại một nơi có gia tốc trọng trường là . Con lắc thực hiện được bao nhiêu dao động trong thời gian là 12 phút.
A. 250. B. 400. C. 500. D. 450.
Lời giải chi tiết

Chọn D.
Bài tập 8: Một con lắc đơn có chiều dài dao động điều hòa với chu kì T tại nơi có gia tốc trọng trường là g. Con lắc đơn có chiều dài dao động điều hòa tại nơi có gia tốc trọng trường với chu kì T' là
![]()
Lời giải chi tiết
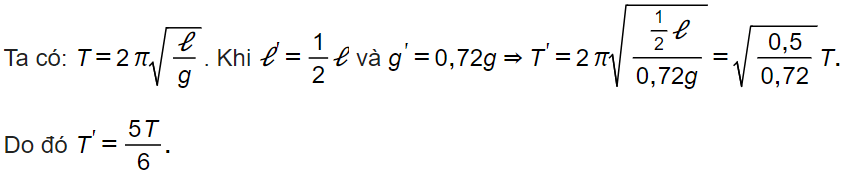
Chọn B.
Bài tập 9: Một con lắc đơn có chu kì T = 0,77 s. Nếu thay đổi chiều dài một lượng là 24 cm thì chu kì của con lắc là T' = 1,155 s. Gia tốc trọng trường tại nơi làm thí nghiệm trên là
![]()
Lời giải chi tiết
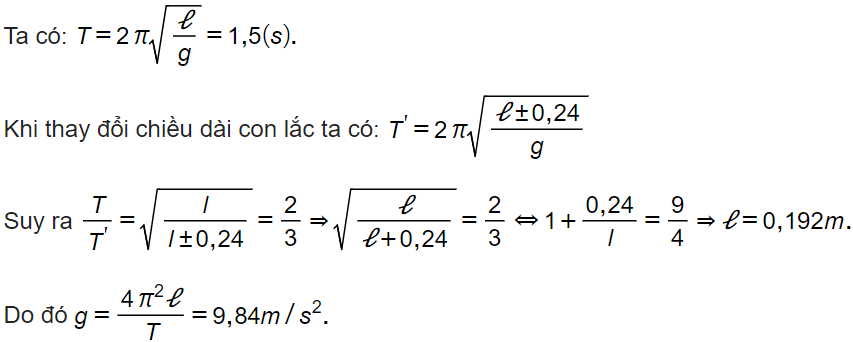
Chọn C.