Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Dao động điều hòa: Lý thuyết và 20 bài tập vận dụng, tài liệu bao gồm có định nghĩa, công thức tính và các dạng bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Vật lí sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi. 

Dao động điều hòa: Lý thuyết và 20 bài tập vận dụng

1. Khái niệm.

     - Dao động cơ: là chuyển động qua lại quanh một vị trí cân bằng ( vị trí hợp lực tác dụng lên vật bằng không). VD: chuyển động đung đưa của chiếc lá,...

     - Dao động tuần hoàn: là dao động cơ mà sau những khoảng thời gian bằng nhau vật trở lại vị trí cũ theo hướng cũ. Khi vật trở lại vị trí cũ theo hướng cũ thì vật thực hiện được một dao động toàn phần. Thời gian vật thực hiện một dao động toàn phần là một chu kỳ T. Số dao động toàn phần vật thực hiện được trong 1s là tần số f.

     - VD: dao động của con lắc đồng hồ. Vị trí B: là vị trí cân bằng của con lắc.

       +) Quá trình từ B → C → B: vật trở về cùng một vị trí nhưng không cùng chiều nên không phải là một dao động toàn phần.

       +) Quá trình B → C → B → A → B: là một dao động toàn phần.

    Dao động điều hòa: là dao động trong đó li đô (vị trí) của vật là một hàm côsin (hay sin) của thời gian.

2. Phương trình dao động điều hòa.

    Điểm P dao động điều hòa trên một đoạn thẳng từ -A đến A luôn có thể coi là hình chiếu của một điểm M chuyển động tròn đều với tốc độ góc ω, trên đường tròn có đường kính là đoạn thẳng đó.

    CM:

    Giả sử t = 0 vật ở vị trí M₀ được xác đinh bằng góc φ

    Tại thời điểm t vị trí của M là (ωt + φ)

    Khi đó hình chiều P của M có tọa độ :

    x = A cos⁡(ωt + φ)

    Phương trình trên được gọi là phương trình của dao động điều hòa.

    Trong đó:

    x: Li độ của vật.

    A: Biên độ của vật ( giá trị lớn nhất của li độ).

    ω: tốc độ góc trong chuyển động tròn đều hay tần số góc trong dao động điều hòa.

    ωt + φ: pha dao động tại thời điểm t.

    φ: pha ban đầu ( pha dao động tại thời điểm ban đầu).

3. Vận tốc, gia tốc của vật dao động điều hòa

    - Vận tốc v = x' = -Aω sin⁡(ωt + φ) = ωA cos⁡(ωt + φ + π/2)

    → Độ lớn v_max = ωA tại vị trí cân bằng x = 0; v = 0 tại vị trí biên x = ±A

    - Gia tốc a = v' = x"= -ω²A = -ω² A cos⁡(ωt + φ) = ω² A cos⁡(ωt+φ + π)

    → Độ lớn a_max = ω² A tại vị trí biên x = ±A; a = 0 tại vị trí cân bằng x = 0

    Nhận xét:

    - Mối quan hệ giữa các giá trị tức thời x, v, a.

       +) Vận tốc v sớm pha hơn li độ x một góc π/2:

       +) Gia tốc a sớm pha hơn vận tốc v một góc π/2:

       +) Gia tốc a và li độ x ngược pha: a = -ω²x

    - Đồ thị của dao động điều hòa: đều là một đường hình sin.

4. Các dạng bài tập Dao động điều hòa

Dạng 1: Xác định các đại lượng trong dao động điều hòa

Phương pháp

Xác định các đại lượng như biên độ A, vận tốc góc ω, chu kỳ, tần số, pha ban đầu, ... bằng cách đồng nhất với phương trình chuẩn của dao động điều hòa.

- Dao động điều hòa là dao động mà li độ của vật được biểu thị bằng hàm cosin hay sin theo thời gian.

Hoặc là nghiệm của phương trình vi phân: x’’ + ω²x = 0 có dạng như sau:

x = Acos(ωt + φ)

Trong đó:

x: Li độ, li độ là khoảng cách từ vật đến vị trí cân bằng ( Đơn vị độ dài)

A: Biên độ (li độ cực đại) ( Đơn vị độ dài)

ω: Vận tốc góc (rad/s)

ωt + φ: Pha dao động (rad/s) tại thời điểm t, cho biết trạng thái dao động của vật ( gồm vị trí và chiều )

φ: Pha ban đầu (rad) tại thời điểm t = 0s, phụ thuộc vào cách chọn gốc thời gian, gốc tọa độ.

φ, A là những hằng số dương;

- Phương trình vận tốc v (m/s)

v = x’ = v = - Aωsin(ωt + φ) = ωAcos(ωt + φ + π/2 )

→ v_max = ωA Tại vị trí cân bằng x = 0

v_min = 0 Tại 2 biên x = 2 hoặc x = -2.

Nhận xét: Trong dao động điều hoà vận tốc sớm pha hơn li độ góc π/2.

- Phương trình gia tốc a (m/s²)

a = v’ = x’’ = a = - ω²Acos(ωt + φ) = - ω²x = ω²Acos(ωt + φ + π/2)

→ a_max = ω²A tại 2 biên

a_min = 0 tại vtcb x = 0

Nhận xét: Trong dao động điều hoà gia tốc sớm pha hơn vận tốc góc π/2 và ngược pha với li độ.

- Chu kỳ: 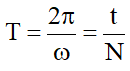 . Trong đó (t: thời gian; N là số dao động thực hiện trong khoảng thời gian t)

“Thời gian để vật thực hiện được một dao động hoặc thời gian ngắn nhất để trạng thái dao động lặp lại như cũ.”

- Tần số: 

“Tần số là số dao động vật thực hiện được trong một giây (số chu kỳ vật thực hiện trong một giây).”

Dạng 2: Mối quan hệ giữa x, v, a, f trong dao động điều hòa

Phương pháp

Dựa vào độ lệch pha giữa 2 đại lượng dao động điều hòa, ta thiết lập nên được mối quan hệ không phụ thuộc thời gian giữa chúng cho dưới bảng sau. Sử dụng các mối quan hệ này để giải quyết những bài toán tìm giá trị tức thời của x, v, a, F khi đã cho 1 trong các đại lượng x, v, a , F.

* Đồ thị biểu diễn các mối quan hệ độc lập với thời gian:

* Hệ thức độc lập:

Chú ý: Việc áp dụng các phương trình độc lập về thời gian sẽ giúp chúng ta giải toán vật lý rất nhanh, do đó, học sinh cần học thuộc dựa vào mối quan hệ của từng đại lượng trong các công thức với nhau và phải vận dụng thành thạo cho các bài toán xuôi ngược khác nhau.

Với hai thời điểm t₁, t₂ vật có các cặp giá trị x₁, v₁ và x₂, v₂ thì ta có hệ thức tính ω, A và T như sau:

* Vật ở VTCB: x = 0; |v|_Max = ωA; |a|_Min = 0.

   Vật ở biên: x = ± A; |v|_Min = 0; |a|_Max = ω²A.

* Sự đổi chiều và đổi dấu của các đại lượng:

   + x, a và F đổi chiều khi qua VTCB, v đổi chiều ở biên.

   + x, a, v và F biến đổi cùng T, f và

• Dạng 3: Viết phương trình dao động điều hòa

• Phương pháp

   

  - Tìm A:

  Trong đó:

  - L là chiều dài quỹ đạo của dao động

  - S là quãng đường vật đi được trong một chu kỳ

  - Tìm ω:

  - Tìm φ

  Cách 1: Dựa vào t = 0 ta có hệ sau:

  

  (Lưu ý: v.φ < 0)

  Cách 2: Sử dụng vòng tròn lượng giác (VLG)

  Góc Φ là góc hợp bởi giữa trục Ox và OM tại thời điểm ban đầu.

  

  Bước 3: Thay kết quả vào phương trình: x = Acos(ωt + Φ ) được phương trình dao động điều hòa của vật.

• Dạng 4: Tìm thời điểm vật qua vị trí x lần thứ n

• Phương pháp

  - Phương trình dao động có dạng: x = Acos(ωt + φ) cm.

  - Phương trình vận tốc có dạng: v = -ωAsin(ωt + φ) cm/s.

  Phương pháp chung:

  a) Khi vật qua li độ x₁ thì:

  x₁ = Acos(ωt + φ) ⇒ cos(ωt + φ) =  = cosb ⇒ ωt + φ = ±b + k2π

  +  với k ∈ N khi b – φ > 0 (v < 0) vật qua x₀ theo chiều âm.

  +  với k ∈ N* khi –b – φ < 0 (v > 0) vật qua x₀ theo chiều dương.

  Kết hợp với điều kiện của bài toán ta loại bớt đi một nghiệm.

  Lưu ý : Ta có thể dựa vào “ mối liên hệ giữa DĐĐH và CĐTĐ ”. Thông qua các bước sau:

  

  • Bước 1: Vẽ đường tròn có bán kính R = A (biên độ) và trục Ox nằm ngang.

  • Bước 2: – Xác định vị trí vật lúc t = 0 thì 

                - Xác định vị trí vật lúc t (x₁ đã biết)

  • Bước 3: Xác định góc quét Δφ =  = ?

  • Bước 4: 

  b) Khi vật đạt vận tốc v₁ thì:

  

  Lưu ý:

  + Đề ra thường cho giá trị n nhỏ, còn nếu n lớn thì tìm quy luật để suy ra nghiệm thứ n.

  + Có thể giải bài toán bằng cách sử dụng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều.

  + Dùng sơ đồ này có thể giải nhanh về thời gian chuyển động, quãng đường đi được trong thời gian Δt, quãng đường đi tối đa, tối thiểu….

  + Có thể áp dụng được cho dao động điện, dao động điện từ.

  + Khi áp dụng cần có kỹ năng biến đổi thời gian đề cho Δt liên hệ với chu kỳ T. và chú ý chúng đối xứng nhau qua gốc tọa độ.

• Dạng 5: Tìm li độ của vật tại thời điểm t

• a) Tìm li độ và hướng chuyển động.

  Vật chuyển động về vị trí cân bằng là nhanh dần (không đều) và chuyển động ra xa vị trí cân bằng là chậm dần (không đều).

  Cách 1:

  

  + v(t₀) > 0: Vật đi theo chiều dương (x đang tăng).

  + v(t₀) < 0: Vật đi theo chiều âm (x đang giảm).

  Cách 2:

  Xác định vị trí trên vòng lượng giác ở thời điểm t₀: ϕ = ωt₀ + φ.

  

  Hạ M xuống trục Ox ta được vị trí của vật ở thời điểm t₀.

  Nếu véctơ quay thuộc nửa trên vòng tròn lượng giác thì hình chiếu chuyển động theo chiều âm (li độ đang giảm).

  Nếu véctơ quay thuộc nửa dưới vòng tròn lượng giác thì hình chiếu chuyển động theo chiều dương (li độ đang tăng).

  Vậy li độ dao động điều hòa: x = A.cosϕ(t₀) = A.cos(ωt₀ + φ)

  Vận tốc dao động điều hòa: v = x’ = -ωAsin ϕ(t₀) = - ωAsin(ωt₀ + φ).

• Dạng 6: Tìm quãng đường, quãng đường lớn nhất, nhỏ nhất (smax, smin) vật đi được

• Phương pháp

  a) Loại 1: Bài toán xác định quãng đường vật đi được trong khoảng thời gian Δt.

  Chú ý:

      + Trong thời gian t = 1T vật đi được quãng đường S = 4A

      + Trong thời gian nửa chu kỳ T vật đi được quãng đường S = 2A

  Bước 1: Xác định vị trí hoặc thời điểm t1, t2 cho trước trên đường tròn. Tìm Δt, Δt = t₂ - t₁.

  Bước 2: Tách Δt = n.T + t* ⇔ Δφ = n.vong + φ*

  Bước 3: Tìm quãng đường. S = n.4.A + S*.

  Căn cứ vào vị trí và chiều chuyển động của vật tại t₁ và t₂ để tìm ra S₃

  

  b) Loại 2: Bài toán xác định S_max - S_min vật đi được trong khoảng thời gian Δt (Δt < T/2 )

  

  Nhận xét:

      + Quãng đường max đối xứng qua VTCB

      + Quãng đường min thì đối xứng qua biên

  BẢNG TÍNH NHANH CÁC GIÁ TRỊ CỰC ĐẠI – CỰC TIỂU CỦA QUÃNG ĐƯỜNG

  Δt	T/6	T/4	T/3	T/2	2T/3	3T/4	5T/6	T
  Smax	A	A√2	A√3	2A	2A + A	2A + A√2	2A + A√3	4A
  Smin	2A - A√3	2A - A√2	A	2A	4A - A√3	4A - A√2	3A	4A

• Dạng 7: Tốc độ trung bình và vận tốc trung bình trong dao động điều hòa

•  Phương pháp

  a) Tổng quát:

  v− = S/t

  Trong đó:

  - S: quãng đường đi được trong khoảng thời gian t

  - t: là thời gian vật đi được quãng đường S

  b. Bài toán tính tốc độ trung bình cực đại của vật trong khoảng thời gian t:

  v_max− = S_max/t

  c. Bài toán tính tốc độ trung bình nhỏ nhất vật trong khoảng thời gian t.

  v_min− = S_min/t

  d. Vận tốc trung bình

  v_tb = Δx/t

  Trong đó:

  Δx: là độ biến thiên độ dời của vật

  t: thời gian để vật thực hiện được độ dời Δx

• Dạng 8: Phương pháp đường tròn hỗn hợp trong dao động điều hòa

•  Phương pháp

  Cùng một dao động: x = Acos(ωt + φ)

  v = v_maxcos(ωt + φ + π/2 ), v_max = Aω.

  a = a_maxcos(ωt + φ + π ), a_max = Aω².

  F = F_maxcos(ωt + φ + π), F_max = m.a_max = mω²A.

  Biểu diễn các đại lượng dao động điều hòa trên cùng một đường tròn có 2 cách là đa điểm hoặc đa trục. Tùy vào từng bài toán mà ta áp dụng đường tròn nào cho phù hợp.

  

• Dạng 9: Tìm thời gian ngắn nhất, lớn nhất vật đi qua li độ, vật có vận tốc, gia tốc

• a) Bài toán tính khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ x₁ đến x₂

  Phương pháp 1: Phương pháp đường tròn lượng giác (khi x có giá trị đặc biệt)

  Ta dùng mối liên hệ giữa DĐĐH và CĐTĐ đều để tính. Khi vật dao động điều hoà từ x₁ đến x₂ thì tương ứng với vật chuyển động tròn đều từ M đến N (chú ý x₁ và x₂ là hình chiếu vuông góc của M và N lên trục Ox.

  Thời gian ngắn nhất vật dao động đi từ x₁ đến x₂ bằng thời gian vật chuyển động tròn đều từ M đến N

  

  Ta vận dụng:

  

  Ta làm theo các bước sau:

  * Bước 1: Vẽ đường tròn có bán kính R = A (biên độ) và trục Ox nằm ngang

  

  * Bước 2 :

  – Xác định vị trí vật lúc t = 0 thì 

  – Xác định vị trí vật lúc t (x_t đã biết)

  * Bước 3 : Xác định góc quét Δφ = ?

  * Bước 4 : 

  Phương pháp 2:

  

  Ngoài ra, nếu vị trí x* là những vị trí đặc biệt, ví dụ như  … thì ta phải ghi nhớ bảng phân bố thời gian và những thời gian đặc biệt nó sẽ giúp chúng ta giải bài toán trắc nghiệm rất nhanh chóng và chính xác.

  Các khoảng thời gian ngắn nhất đặc biệt:

  

  Vật 2 lần liên tiếp đi qua  thì  .

• Dạng 11: Bài toán liên quan đến số lần hai vật gặp nhau

• Phương pháp

  a) Dạng bài toán liên quan đến số lần hai vật gặp nhau.

  Phương pháp:

  Cách nhớ nhanh số lần hai vật gặp nhau của 2 vật dao động điều hòa có cùng tần số góc nhưng không cùng biên độ.

  Hai vật phải cùng vị trí cân bằng O, biểu diễn bằng hai đường tròn đồng tâm (hình vẽ). Khi gặp nhau thì hình chiếu của hai vecto quay  biểu diễn chúng trên trục hoành trùng nhau. Tức là MN luôn vuông góc với trục Ox tại thời điểm gặp nhau.

  

  Giả sử lần gặp nhau ban đầu hai chất điểm ở vị trí có tọa độ x vào thời điểm t₁.

  Vì hai dao động cùng tần số nên tại mọi thời điểm góc MON luôn không đổi và bằng:  (trong đó φ₁, φ₂ lần lượt là pha ban đầu dao động của vật M và vật N) và tam giác MON luôn cùng quanh O với tốc độ góc ω. Do đó từ vòng tròn lượng giác, ta nhận thấy rằng cứ sau khoảng thời gian T/2 thì ∆MON lại có cạnh MN vuông góc với OX, tức là hai vật lại gặp nhau.

  + Vậy khoảng thời gian liên tiếp để chúng gặp nhau là T/2.

  * Đầu tiên ta tìm khoảng thời gian nhỏ nhất từ lúc t = 0 đến khi hai vật gặp nhau bằng hình học:

  Sử dụng định lý Hàm số cosin trong tam giác MON ta tính được cạnh MN

  

  Sử dụng định lý hàm số sin (hoặc dùng định lý hàm số côsin) ta tìm được góc α

  

  Như vậy ta tìm được pha dao động của N tại thời điểm gặp nhau:

   (vì sau một nữa vòng ta lại có thời điểm gặp nhau, lấy dấu (+) nếu vật 2 nhanh pha hơn vật 1, lấy dấu (-) cho trường hợp vật 2 chậm pha hơn vật 1)

  Ta có:  , ta tìm được nghiệm t dương nhỏ nhất là tm.

  Vậy số lần gặp nhau sau thời thời gian t được xác định như sau:

  Phân tích: t = t_m + n.T/2 + ∆t_m (0 < ∆t_m < T/2).

  Vậy số lần gặp nhau là: n + 1 lần.

  b. Các trường hợp gặp nhau của hai vật dao động cùng tần số, khác biên độ.

  Phương pháp:

  Có hai vật dao động điều hòa trên hai đường thẳng song song, sát nhau, với cùng một chu kì. Vị trí cân bằng của chúng sát nhau.

  

  Biên độ dao động tương ứng của chúng là A₁ và A₂ (giả sử A₁ > A₂). Tại thời điểm t = 0, chất điểm thứ nhất có li độ x₁ chuyển động theo chiều dương, chất điểm thứ hai có li độ x₂ chuyển động theo chiều dương.

  1. Hỏi sau bao lâu thì hai chất điểm gặp nhau? Chúng gặp nhau tại li độ nào?

  2. Với điều kiện nào thì khi gặp nhau, hai vật chuyển động cùng chiều? Ngược chiều? Tại biên?

  Có thể xảy ra các khả năng sau (với  , c là độ dài của cạnh MN):

  

  c. Các trường hợp đặc biệt:

  Hai vật dao động cùng tần số, vuông pha nhau (độ lệch pha  )

  - Đồ thị biểu diễn sự phụ thuộc giữa chúng có dạng elip.

  - Kết hợp với:  , suy ra: 

  Đặc biệt: Khi A = A₁ = A₂ (hai vật có cùng biên độ hoặc một vật ở hai thời điểm khác nhau), ta có:  (lấy dấu + khi k lẻ và dấu – khi k chẵn).

• Dạng 12: Bài toán Hai vật dao động điều hòa khác tần số cùng biên độ

• Phương pháp

  a) Xác định khoảng thời gian ngắn nhất để 2 vật cùng trở lại trạng thái lúc đầu:

  Gọi n₁ và n₂ là số dao động toàn phần mà 2 vật thực hiện được cho đến lúc trở lại trạng thái đầu.

  Thời gian từ lúc xuất phát đến lúc trở lại trạng thái đầu là: Δt = n₁T₁ = n₂T₂. (n₁, n₂ ∈ N*).

  Tìm n_1min, n_2min thoả mãn biểu thức trên ⇒ giá trị Δt_min cần tìm.

  b) Xác định khoảng thời gian ngắn nhất để 2 vật vị trí có cùng li độ.

  Xác định pha ban đầu φ của hai vật từ điều kiện đầu x₀ và v.

  Giả sử T₁ > T₂ nên vật 2 đi nhanh hơn vật 1, chúng gặp nhau tại x₁

   

  

• Dạng 13: Tìm số lần vật đi qua vị trí có li độ x, có vận tốc v từ thời điểm t1 đến t2

• Phương pháp

  * Giải phương trình lượng giác được các nghiệm

  * Từ t₁ < t ≤ t₂ ⇒ Phạm vi giá trị của (với k ∈ Z)

  * Tổng số giá trị của k chính là số lần vật đi qua vị trí đó.

  Lưu ý:

  + Có thể giải bài toán bằng cách sử dụng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều.

  + Trong mỗi chu kỳ (mỗi dao động) vật qua mỗi vị trí biên 1 lần còn các vị trí khác 2 lần.

5. Bài tập vận dụng

Câu 1. Một chất điểm tham gia đồng thời 2 dao động điều hòa cùng phương trên trục Ox có phương trình x₁ = 2√3sinωt (cm) và x₂ = A₂cos(ωt + φ₂) (cm). Phương trình dao động tổng hợp x = 2cos(ωt + φ)(cm), với φ₂ - φ = π/3. Biên độ và pha ban đầu của dao động thành phần 2 là:

A. A₂ = 4 cm; φ₂ = π/6

B. A₂ = 4 cm; φ₂ = π/3

C. A₂ = 2√3 cm; φ₂ = π/4

D. A₂ = 4√3 cm; φ₂ = π/3

Lời giải:

Viết lại phương trình dao động của thành phần 1:

Câu 2. Cho hai dao động điều hoà cùng phương: x₁ = 2cos(4t + φ₁)cm và x₂ = 2cos(4t + φ₂)cm. Với 0 ≤ φ₂ - φ₁ ≤ π. Biết phương trình dao động tổng hợp x = 2 cos (4t + π/6) cm. Pha ban đầu φ₁ là:

A. π/2      B. -π/3     C. π/6       D. -π/6

Lời giải:

Câu 3. Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số có phương trình li độ x = 3cos(πt – 5π/6) (cm). Biết dao động thứ nhất có phương trình li độ x₁ = 5cos(πt + π/6) (cm). Dao động thứ hai có phương trình li độ là

A. x₂ = 8cos(πt + π/6) cm

B. x₂ = 2cos(πt + π/6) cm

C. x₂ = 2cos(πt – 5π/6) cm

D. x₂ = 8cos(πt – 5π/6) cm

Lời giải:

Nhận xét: ta thấy biên độ và pha đều cho rõ ràng nên cách giải nhanh nhất là dùng máy tính.

Câu 4. Một chất điểm tham gia đồng thời hai dao động có các phương trình: x₁ = A₁cos(ωt + π/2) (cm); x₂ = 5 cos(ωt + φ)(cm). Phương trình dao động tổng hợp là x = 5√3cos(ωt + π/3). Giá trị của A₁ bằng

A. 5,0 cm hoặc 2,5 cm.

B. 2,5√3 cm hoặc 2,5 cm

C. 5,0 cm hoặc 10 cm

D. 2,5√3 cm hoặc 10 cm

Lời giải:

Áp dụng định lý hàm số cosin cho tam giác OA₁A

Câu 5. Một chất điểm tham gia đồng thời hai dao động có các phương trình: x₁ = A₁cos(ωt + π/2) (cm); x₂ = 5 cos(ωt + φ)(cm). Phương trình dao động tổng hợp là x = 5√3cos(ωt + π/3). Giá trị của A₁ bằng

A. 5,0 cm hoặc 2,5 cm.

B. 2,5√3 cm hoặc 2,5 cm

C. 5,0 cm hoặc 10 cm

D. 2,5√3 cm hoặc 10 cm

Lời giải:

Câu 6. Cho hai dao động điều hoà cùng phương: x₁ = 2cos(4t + φ₁)cm và x₂ = 2cos(4t + φ₂)cm. Với 0 ≤ φ₂ - φ₁ ≤ π. Biết phương trình dao động tổng hợp x = 2cos(4t + π/6) cm. Pha ban đầu φ₁ là:

A. π/2     B. -π/3     C. π/6     D. -π/6

Lời giải:

Chọn D

Câu 7. Hai dao động cùng phương lần lượt có phương trình x₁ = A₁cos(πt + π/6)(cm) và x₂ = 6cos(πt - π/2) (cm). Dao động tổng hợp của hai dao động này có phương trình x = Acos(πt + φ) (cm). Thay đổi A₁ cho đến khi biên độ A đạt giá trị cực tiểu thì

A. φ = -π/6 rad     B. φ = π rad

C. φ = -π/3 rad      D. φ = 0 rad

Lời giải:

Vẽ giản đồ như hình vẽ.

Theo định lí hàm sin:

⇒ A đạt giá trị cực tiểu khi sin(π/6 - φ) = 1

Do đó φ = -π/3

Câu 8. Cho hai phương trình dao động điều hòa cùng phương cùng tần số có phương trình x₁ = A₁cos(4πt - π/6) cm và x₂ = A₂cos(4πt - π) cm. Phương trình dao động tổng hợp x = 9cos(4πt - φ) cm. Biết biên độ A₂ có giá trị cực đại. Giá trị của A₁ và phương trình dao động tổng hợp là:

A. x = 9√2cos(4πt - π/4) cm

B. x = 9√2cos(4πt + 3π/4) cm

C. x = 9cos(4πt - 2π/3) cm

D. x = 9cos(4πt + π/3) cm

Lời giải:

Vẽ giản đồ vectơ

Dựa vào giản đồ vectơ. Áp đụng định lý hàm số sin

Từ (1) ⇒ khi α = 90°: A₂ = A/(1/2) = 2A = 18 cm

Tam giác OAA₂ vuông tại A, nên ta có:

Xác định pha ban đầu tổng hợp

Dựa vào giản đồ vec tơ: φ = π/2 + π/6 = 2π/3

Vậy phương trình dao động tổng hợp là: C. x = 9cos(4πt - 2π/3) cm

Câu 9. Hai dao động điều hoà cùng phương, cùng tần số có phương trình dao động x₁ = A₁cos(ωt + π/3) cm và x₂ = A₂cos(ωt - π/2) cm. Phương trình dao động tổng hợp của hai dao động này là: x = 6cos(ωt + φ) cm. Biên độ A₁ thay đổi được. Thay đổi A₁ để A₂có giá trị lớn nhất. Tìm A_2max?

A. 16 cm     B. 14 cm     C. 18 cm     D. 12 cm

Lời giải:

Độ lệch pha giữa 2 dao động: Δφ = 5π/6 rad không đổi.

Biên độ của dao động tổng hợp A = 6 cm cho trước.

Biểu diễn bằng giản đồ vectơ như hình vẽ

Ta có:

Vì α, A không đổi nên A₂ sẽ lớn nhất khi sinβ lớn nhất tức là góc β = 90°.

Khi đó

Câu 10. Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, theo các phương trình x₁ = 3cos(4t + π/2) cm và x₂ = A₂cos(4t) cm. Biết khi động năng của vật bằng một phần ba năng lượng dao động thì vật có tốc độ 8√3 cm/s. Biên độ A₂ bằng

A. 1,5 cm      B. 3 cm      C. 3√2 cm     D. 3√3 cm.

Lời giải:

Ta có

Câu 11. Một vật thực hiện đồng thời 3 dao động điều hòa cùng phương cùng tần số có phương trình là x₁, x₂, x₃. Biết x₁₂ = 6cos(πt + π/6) cm; x₂₃ = 6cos(πt + 2π/3) cm; x₁₃ = 6√2cos(πt + π/4) cm. Khi li độ của dao động x₁ đạt giá trị cực đại thì li độ của dao động x₃ là:

A. 0 cm       B. 3 cm     C. 3√2 cm     D. 3√6 cm

Lời giải:

Ta thấy x₃ sớm pha hơn x₁ góc π/2 ⇒ x₁ max thì x₃ = 0.

Câu 12. Hai vật dao động điều hòa với phương trình x₁ = A₁cos20πt (cm), x₂ = A₂cos20πt (cm). Tính từ thời điểm ban đầu, thì cứ sau 0,125s thì khoảng cách 2 vật lại bằng A₁. Biên độ A₂ là

Lời giải:

+ Điều kiện để khoảng cách giữa hai vật là A₁ thì A₂ > A₁, lúc đó phương trình khoảng cách: Δx = x₂ – x₁ = (A₂ – A₁)cos20πt₁    (⋇)

+ Ở thời điểm t₁ + 0,125s có:

(A₂ – A₁)cos20π(t₁ + 0,125) = A₁ ⇔ (A₂ – A₁)cos(20πt₁ + 2,5π) = A₁      (⋇⋇)

+ Từ (⋇) và (⋇⋇): tan20πt₁ = 1 ⇒ tan20πt₁ = √2/2 thay vào (⋇) ta có được: 

Câu 13. Hai chất điểm M và N dao động điều hòa cùng chu kì T = 4s dọc theo hai đường thẳng song song kề nhau và song song với trục Ox. Vị trí cân bằng của M và N đều ở trên cùng một đường thẳng qua gốc tọa độ và vuông góc với Ox. Trong quá trình dao động, khoảng cách lớn nhất giữa M và N theo phương Ox là 10 cm. Tại thời điểm t₁ hai vật đi ngang qua nhau, hỏi sau thời gian ngắn nhất là bao nhiêu kể từ thời điểm t₁ khoảng cách giữa chúng bằng 5√2 cm

A. 1 s     B. 1/3 s      C. 1/2 s      D. 1/6 s

Lời giải:

+ Chọn gốc thời gian là thời điểm hai vật đi ngang qua nhau thì phương trình khoảng cách giữa hai vật có thể chọn Δx = x₂ - x₁ = 10sin(0,5πt) cm

+ Thời gian ngắn nhất để hai vật cách nhau 5 cm là thời gian ngắn nhất đi từ Δx = 0 đến Δx = 5 cm là: T/8 = 1/2 s.

Câu 14. Cho hai phương trình dao động điều hòa cùng phương cùng tần số có phương trình x₁ = A₁cos(4πt - π/6) cm và x₂ = A₂cos(4πt - π) cm. Phương trình dao động tổng hợp x = 9cos(4πt - φ) cm. Biết biên độ A₂ có giá trị cực đại. Giá trị của A₁; A₂ và φ là:

A. A₁ = 9√3 cm; A₂ = 18 cm; φ = -2π/3 rad

B. A₁ = 9 cm; A₂ = 9√3 cm; φ = π/3 rad

C. A₁ = 9√3 cm; A₂ = 9 cm; φ = 2π/3 rad

D. A₁ = 9 cm; A₂ = 18 cm; φ = -π/3 rad

Lời giải:

Độ lệch pha giữa thành phần tổng hợp với

Thành phần thứ hai: φ - φ₂ = -π/3 + π/2 = π/6

Theo định lý hàm sin:

Ta lại có: A₁² = A² + A₂² - 2AA₂cos(φ - φ₂) ⇔ A₂² - 2A₁A₂cos(π/6) = 0

⇒ A₂ = √3A₁ = 10√3 cm. Chọn A.

Câu 15. (ĐH 2014) Cho hai dao động điều hòa cùng phương với các phương trình lần lượt là x₁ = A₁cos(ωt + 0,35) cm và x₂ = A₂cos(ωt - 1,57) cm . Dao động tổng hợp của hai dao động này có phương trình là x = 20cos(ωt + φ). Giá trị cực đại của (A₁ + A₂) gần giá trị nào nhất sau đây?

A. 25 cm     B. 20 cm     C. 40 cm     D. 35 cm

Lời giải:

Theo bài ra:

Áp dụng định lí hàm số sin:

⇒ ΔOMB cân tại M

. Chọn D

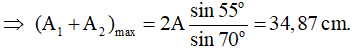
Câu 16. (Trích đề thi thử chuyên Hà Tĩnh lần 2 năm 2013): Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số có biên độ bằng trung bình cộng của hai biên độ thành phần và lệch pha so với dao động thành phần thứ nhất là 90°. Độ lệch pha của hai dao động thành phần đó là:

A. 120°     B. 126,9°     C. 105°     D. 143,1°

Lời giải:

Áp dụng định lý hàm sin:

Chọn B

Câu 17: Một vật thực hiện đồng thời 3 dao động điều hòa cùng phương cùng tần số có phương trình là x₁, x₂, x₃. Biết x₁₂ = 6cos(πt + π/6) cm; x₂₃ = 6cos(πt + 2π/3) cm; x₁₃ = 6√2cos(πt + 5π/12) cm. Tính x biết x² = x₁² + x₃²

A. 6√2 cm     B. 12 cm      C. 24 cm     D. 6√3 cm

Lời giải:

Sử dụng máy tính fx 570Es (plus) ta được:

Chọn A

Câu 18. Cho ba vật dao động điều hòa cùng tần số, cùng khối lượng, dao động trên những trục song song kề nhau và song song với trục Ox với phương trình lần lượt x₁ = Acos(ωt + φ₁) cm, x₂ = Acos(ωt + φ₂) cm và x₃ = Acos(ωt + φ₃) cm. Biết tại mọi thời điểm thì động năng của chất điểm thứ nhất luôn bằng thế năng của chất điểm thứ hai và li độ của ba chất điểm thỏa mãn hệ thức -x₁² = x₂.x₃. Tại thời điểm mà khoảng cách giữa x₂ và x₃ bằng 2A/√3 thì tỉ số giữa động năng của chất điểm thứ nhất so với chất điểm thứ ba là

A. 9/11     B. 11/9     C. 9/4     D. 4/9

Lời giải:

+ Ta có E_đ1 = E_t2 ⇔ mω²(A² - x₁²) = mω²x₂² ⇔ x₁² + x₂² = A²

+ Tại mọi thời điểm : -x₁² = x₂.x₃ ⇒ x₂² - A² = x₂x₃ ⇔ x₂(x₂ - x₃) = A²

+ Khi khoảng cách giữa hai chất điểm 2 và 3 là 2A/√3 ta có :

Chọn A

Câu 19. Một chất điểm tham gia đồng thời ba dao động điều hòa có phương trình x₁ = 2cos(ωt) cm; x₂ = 2cos(ωt + φ₂) cm và x₃ = 2cos(ωt + φ₃) cm với φ₃ ≠ φ₂ và 0 ≤ φ₃; φ₂ ≤ π. Dao động tổng hợp của x₁ và x₂ có biên độ là 2 cm, dao động tổng hợp của x₁ và x₃ có biên độ 2√3 cm. Độ lệch pha giữa hai dao động x₂ và x₃ là

A. 5π/6      B. π/3     C. π/2      D. 2π/3

Lời giải:

Nhận thấy biên độ các dao động thành phần bằng nhau nên:

Chọn B

Câu 20. Hai vật dao động điều hòa cùng phương, cùng tần số có phương trình lần lượt là x₁ = A₁cos(ωt + φ₁) và x₂ = A₂cos(ωt + φ₂). Gọi x₍₊₎ = x₁ + x₂ và x_(-) = x₁ - x₂. Biết rằng biên độ dao động của x₍₊₎ gấp 3 lần biên độ dao động của x_(-). Độ lệch pha cực đại giữa x₁ và x₂ gần nhất với giá trị nào sau đây ?

A. 50°     B. 40°     C. 30°     D. 60°

Lời giải:

+ Ta có:

+ Mà: A₍₊₎ = 3A_(-) ⇒ 20A₁A₂cosΔφ = 8(A₁² + A₂²) ≥ 16A₁₂

Vậy giá trị gần nhất với Δφ_max là 40°. Chọn B

Câu 21. (Chuyên Lương Văn Tụy – Ninh Bình lần 2/2016) Ba chất điểm M₁, M₂ và M₃ dao động điều hòa trên ba trục tọa độ song song cách đều nhau với các gốc tọa độ tương ứng O₁, O₂ và O₃ như hình vẽ. Khoảng cách giữa hai trục tọa độ liên tiếp là a = 2 cm. Biết rằng phương trình dao động của M₁ và M₂ là x₁ = 3cos2πt (cm) và x₂ = 1,5cos(2πt + π/3) (cm). Ngoài ra, trong quá trình dao động, ba chất điểm luôn luôn thẳng hàng với nhau. Khoảng cách lớn nhất giữa hai chất điểm M₁ và M₃ gần giá trị nào nhất sau đây?

A. 6,56 cm

B. 5,20 cm

C. 5,57 cm

D. 5,00 cm

Lời giải:

+ Điều kiện để 3 chất điểm luôn thẳng hàng là: x₂ = (x₁ + x₃)/2

+ Khoảng cách cực đại giữa hai chất điểm M₁ và M₃ là:

Chọn A

Câu 22. Một vật tham gia đồng thời hai dao động điều hoà cùng phương, cùng tần số và có dạng phương trình x₁ = √3cos(4t + φ₁) cm, x₂ = 2cos(4t + φ₂) cm với 0 ≤ φ₁ − φ₂ ≤ π. Biết phương trình dao động tổng hợp x = cos(4t + π/6) cm. Giá trị φ₁ là

A. 2π/3     B. –π/6       C. π/6     D. −2π/3

Lời giải:

Ta có 1 = 3 + 4 + 2(√3).2.cosΔφ

⇒ Δφ = 5π/6 = φ₁ - φ₂

⇒ φ₂ = φ₁ - 5π/6

Câu 23. Cho hai dao động điều hoà cùng phương có phương trình dao động lần lượt là x₁ = 3√3sin(5πt + π/2)(cm) và x₂ = 3√3sin(5πt - π/2)(cm). Biên độ dao động tổng hợp của hai dao động trên bằng

A. 0 cm     B. 3 cm     C. 63 cm     D. 33 cm

Lời giải:

Hai dao động trên ngược pha nhau vì Δφ = φ₂-φ₁ = -π nên biên độ dao động tổng hợp sẽ là: A = |A₂ - A₁| = 0.

Câu 24. Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là x₁ = 3cos10t (cm) và x₂ = 4sin(10t + π/2)(cm). Gia tốc của vật có độ lớn cực đại bằng

A. 7 m/s²     B. 3 m/s²     C. 6 m/s²     D. 13 m/s²

Lời giải:

Đưa phương trình li độ của dao động thứ 2 về dạng chuẩn theo cos: x₂ = 4sin(10t + π/2) = 4cos(10t)

Từ đây ta thấy rằng: hai dao động trên cùng pha vì thế biên độ dao động tổng hợp: A = A₁ + A₂ = 3 + 4 = 7 (cm)

Gia tốc có độ lớn cực đại: a_max = ω²A = 100.7 = 700 cm/s² = 7 m/s²

Câu 25. Dao động của một chất điểm có khối lượng 100 g là tổng hợp của hai dao động điều hòa cùng phương, có phương trình li độ lần lượt là x₁ = 5cos(10t) và x₂ = 10cos(10t) (x₁ và x₂ tính bằng cm, t tính bằng s). Mốc thế năng ở vị trí cân bằng. Cơ năng của chất điểm bằng

A. 0,1125 J     B. 225 J     C. 112,5 J     D. 0,225 J

Lời giải:

Hai dao động trên cùng pha vì thế biên độ dao động tổng hợp: A = A₁ + A₂ = 5 + 10 = 15 cm

Cơ năng của chất điểm: E = (1/2).m.ω²A² = (1/2). 0,1. 10².0,15² = 0,1125 J

Câu 26. Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là x₁ = 4cos(10t + π/4)(cm) và x₂ = 3cos(10t - 3π/4)(cm). Độ lớn vận tốc của vật ở vị trí cân bằng là

A. 100 cm/s     B. 50 cm/s

C. 80 cm/s     D. 10 cm/s

Lời giải:

Ta có: Δφ = φ₂-φ₁ = (-3π/4)-π/4 = -π ⇒ hai dao động trên ngược pha

Biên độ dao động tổng hợp: A = |A₁ - A₂| = 1 cm

Vận tốc của ở VTCB là: v_VTCB = v_max = ωA = 10.1 = 10 cm/s . Chọn D

Câu 27. Dao động của một vật là tổng hợp của hai dao động cùng phương có phương trình lần lượt là x₁ = Acosωt và x₂ = Asinωt. Biên độ dao động của vật là

A. √3A     B. A     C. √2A     D. 2A

Lời giải:

Chuyển phương trình của thành phần thứ 2 về dạng chuẩn theo cos: x₂ = Asinωt = Acos(ωt - π/2)

Câu 28. Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số có biên độ bằng nhau và bằng A nhưng pha ban đầu lệch nhau π/3 rad. Dao động tổng hợp có biên độ là

A. 1 A     B. √2A     C. 2A     D. √3A

Lời giải:

Biên độ dao động tổng hợp:

Theo bài ra thì hai dao động lệch pha nhau π/3 nên cos(φ₁ - φ₂) = cos(π/3) = 1/2

Vì thế biên độ dao động sẽ là:

Câu 29. Một vật thực hiện đồng thời 2 dao động điều hoà cùng phương, cùng tần số có phương trình: x₁ = √3cos(ωt - π/2) cm, x₂ = cos(ωt) cm. Phương trình dao động tổng hợp:

A. x = 2√2cos(4πt - π/4) cm

B. x = 2√2cos(4πt + 3π/4) cm

C. x = 2cos(4πt - π/3) cm

D. x = 2cos(4πt + π/3) cm

Lời giải:

Câu 30. Một vật tham gia đồng thời ba dao động điều hòa cùng phương với các phương trình: x₁ = 5cos5πt (cm); x₂ = 3cos(5πt + π/2) (cm) và x₃ = 8cos(5πt - π/2) (cm). Xác định phương trình dao động tổng hợp của vật.

A. x = 5√2cos(5πt - π/4) cm

B. x = 5√2cos(5πt + 3π/4) cm

C. x = 5cos(5πt - π/3) cm

D. x = 5cos(5πt + 2π/3) cm

Lời giải:

Cách 1: Ta có: x₁ = 3sin(5πt + π/2) (cm) = 3cos5πt (cm)

x₂ và x₃ ngược pha nên: A₂₃ = 8 - 3 = 5 ⇒ x₂₃ = 5cos(5πt - π/2) (cm)

x₁ và x₂₃ vuông pha. Vậy: x = x₁ + x₂ + x₃ = 5√2cos(5πt - π/4) (cm)

Cách 2: Với máy FX570ES:

Câu 31. Dao động tổng hợp của hai dao động điều hòa cùng phương có biểu thức x = 5√3cos(6πt + π/2) (cm). Dao động thứ nhất có biểu thức là x₁ = 5cos(6πt + π/3)(cm). Tìm biểu thức của dao động thứ hai.

A. x₂ = 5√2cos(6πt - π/4) cm

B. x₂ = 5√2cos(6πt + 3π/4) cm

C. x₂ = 5cos(6πt - π/3) cm

D. x₂ = 5cos(6πt + 2π/3) cm

Lời giải:

Cách 1:

Cách 2: Với máy FX570ES :