Với giải Bài 2 trang 25 Toán 9 Tập 1 Cánh diều chi tiết trong Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn
Bài 2 trang 25 Toán 9 Tập 1: Giải hệ phương trình sau bằng phương pháp cộng đại số:
a. ;
b. ;
c. ;
d. .
Lời giải:
a.
Cộng từng vế hai phương trình (1) và (2), ta nhận được phương trình:
, tức là
Thế vào phương trình (2), ta nhận được phương trình: (3)
Giải phương trình (3), ta có: .
Vậy hệ phương trình đã cho có nghiệm .
b.
Nhân hai vế của phương trình (2) với 2 và giữ nguyên phương trình (1), ta được hệ phương trình sau:
Trừ từng vế hai phương trình (3) và (4), ta nhận được phương trình: (5)
Giải phương trình (5), ta có:
Thế giá trị vào phương trình (2), ta được phương trình: (6)
Giải phương trình (6):
Vậy hệ phương trình đã cho có nghiệm .
c.
Chia hai vế của phương trình (1) với và giữ nguyên phương trình (2), ta được hệ phương trình sau:
Trừ từng vế của phương trình (3) và (4), ta nhận được phương trình: (5)
Do đó phương trình (5) có vô số nghiệm.
Vậy hệ phương trình đã cho có vô số nghiệm.
d.
Chia hai vế của phương trình (2) với và giữ nguyên phương trình (1), ta được hệ phương trình sau:
Trừ từng vế của phương trình (3) và (4), ta nhận được phương trình: (5)
Do đó phương trình (5) vô nghiệm.
Vậy hệ phương trình đã cho có vô nghiệm.
Sơ đồ tư duy Giải hệ hai phương trình bậc nhất hai ẩn
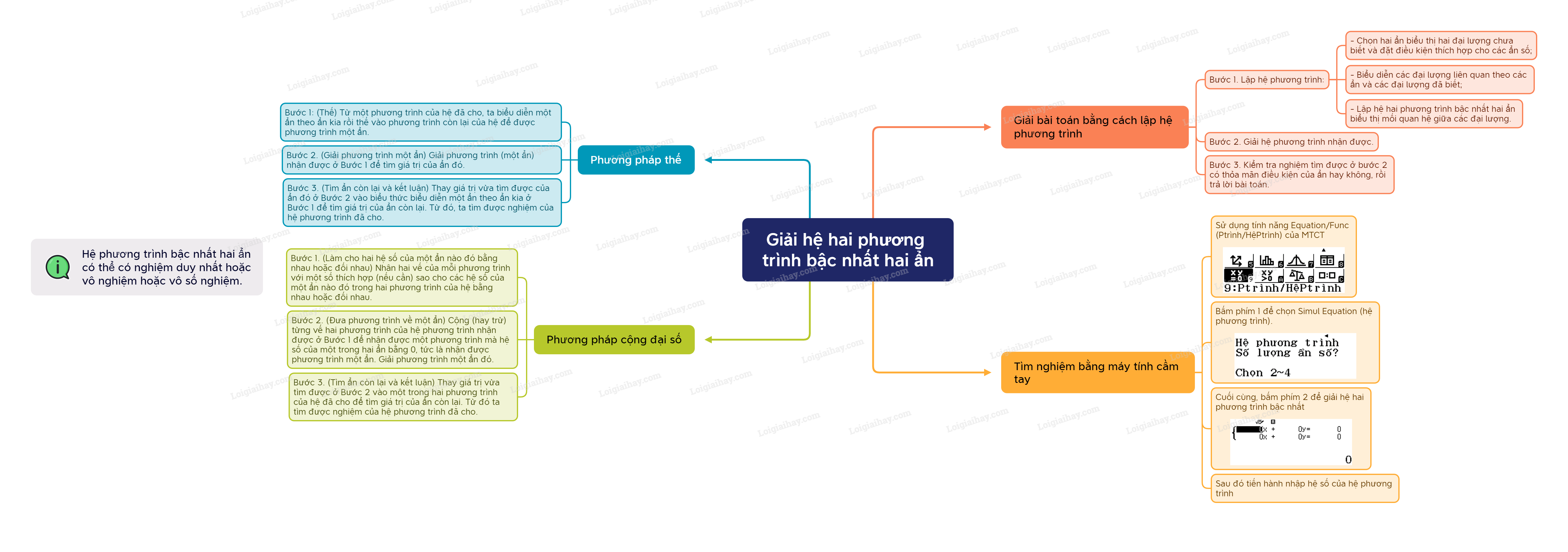
Xem thêm lời giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:
Luyện tập 3 trang 21 Toán 9 Tập 1: Giải phương trình: .....
Luyện tập 4 trang 21 Toán 9 Tập 1: Giải hệ phương trình: .....
Luyện tập 5 trang 23 Toán 9 Tập 1: Giải bài toán ở phần mở đầu.......
Luyện tập 6 trang 24 Toán 9 Tập 1: Sử dụng máy tính cầm tay để tìm nghiệm của hệ phương trình:.....
Xem thêm các bài giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:
§2. Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn
§3. Giải hệ hai phương trình bậc nhất hai ẩn