Giải SGK Toán 9 Bài 2 (Cánh diều): Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

Van Anh Ngày: 23-09-2024 Lớp 9

816

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 2: Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn chi tiết sách Toán 9 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 2: Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

Khởi động trang 12 Toán 9 Tập 1: Một lạng thịt bò chứa 26g protein, một lạng thịt cá chứa 22g protein. Bác An dự định chỉ bổ sung 70g protein từ thịt bò và thịt cá trong một ngày.

Toán 9 Bài 2 (Cánh diều): Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn (ảnh 1)

Số lạng thịt bò và số lạng thịt cá mà bác An ăn trong một ngày cần thỏa mãn điều kiện ràng buộc gì để đáp ứng nhu cầu bổ sung protein của bác An?

Lời giải:

Ta thấy số lạng thịt bò và số lạng thịt cá nhân với lượng protein phải bằng 70g protein bác An muốn bổ sung

1. Phương trình bậc nhất hai ẩn

Hoạt động 1 trang 12 Toán 9 Tập 1: Trong bài toán ở phần mở đầu, ta gọi $x, y$ lần lượt là số lạng thịt bò và số lạng thịt cá mà bác An ăn trong một ngày. Viết hệ thức liên hệ giữa $x$ và $y$ để đáp ứng nhu cầu bổ sung protein của bác An.

Lời giải:

+ Lượng protein mà $x$ lạng thịt bò bác An ăn trong một ngày cung cấp là: $26 x$ (g);

+ Lượng protein mà $y$ lạng thịt các bác An ăn trong một ngày cung cấp là: $22 y$ (g);

+ Để đáp ứng nhu cầu bổ sung protein của bác An, $x$ và $y$ cần thỏa mãn: $26 x + 22 y = 70$ .

Luyện tập 1 trang 12 Toán 9 Tập 1: Nêu hai ví dụ về phương trình bậc nhất hai ẩn.

Lời giải:

Ví dụ: $2 x + 3 y = 1; x + y = - 2$ .

Hoạt động 2 trang 13 Toán 9 Tập 1: Cho phương trình bậc nhất hai ẩn $x, y$ :

$3 x - 2 y = 6 (1)$

Tính giá trị của biểu thức ở vế trái của phương trình (1) tại $x = 4; y = 3$ . Giá trị đó có bằng 6 hay không?

Lời giải:

Tại $x = 4; y = 3$ biểu thức $3 x - 2 y$ có giá trị bằng:

$3.4 - 2.3 = 12 - 6 = 6$ .

Luyện tập 2 trang 13 Toán 9 Tập 1: Nêu hai nghiệm của phương trình: $6 x - 5 y = 11$ .

Lời giải:

Hai nghiệm của phương trình đã cho là: $(1; - 1); (2; \frac{1}{5})$

2. Hệ hai phương trình bậc nhất hai ẩn

Hoạt động 3 trang 16 Toán 9 Tập 1: Hai bạn Dũng, Huy vào siêu thị mua vở và bút bi để ủng hộ các bạn học sinh vùng lũ lụt. Bạn Dũng mua 5 quyển vở và 3 chiếc bút bi với tổng số tiền phải trả là 39 000 đồng. Bạn Huy mua 6 quyển vở và 2 chiếc bút bi với tổng số tiền phải trả là 42 000 đồng. Giả sử giá của mỗi quyển vở là $x$ đồng $(x > 0)$ , giá của mỗi chiếc bút bi là $y$ đồng $(y > 0)$ .

a. Viết hai phương trình bậc nhất hai ẩn $x, y$ lần lượt biểu thị tổng số tiền phải trả của bạn Dũng, bạn Huy.

b. Cặp số $(x; y) = (6 000; 3 000)$ có phải là nghiệm của từng phương trình bậc nhất đó hay không? Vì sao?

Lời giải:

+ Bạn Dũng phải trả số tiền cho 5 quyển vở là: $5 x$ (đồng);

+ Bạn Dũng phải trả số tiền cho 3 chiếc bút bi là: $3 y$ (đồng);

Suy ra Số tiền bạn Dũng phải trả là: $5 x + y = 39000$ .

+ Bạn Huy phải trả số tiền cho 6 quyển vở là: $6 x$ (đồng);

+ Bạn Huy phải trả số tiền cho 2 chiếc bút bi là: $2 y$ (đồng);

Suy ra Số tiền bạn Huy phải trả là: $6 x + 2 y = 42000$ .

+ Thay cặp số $(x; y) = (6000; 3000)$ vào phương trình $5 x + y = 39000$ ta được:

$\begin{array}{l} 5.6000 + 3.3000 = 39000 \\ 30000 + 9000 = 39000 \end{array}$

$39000 = 39000$ (luôn đúng).

Vậy cặp số $(x; y) = (6000; 3000)$ là nghiệm của phương trình $5 x + y = 39000$ .

+ Thay cặp số $(x; y) = (6000; 3000)$ vào phương trình $6 x + 2 y = 42000$ ta được:

$\begin{array}{l} 6.6000 + 2.3000 = 42000 \\ 36000 + 6000 = 42000 \end{array}$

$42000 = 42000$ (luôn đúng).

Vậy cặp số $(x; y) = (6000; 3000)$ là nghiệm của phương trình $6 x + 2 y = 42000$ .

Luyện tập 3 trang 16 Toán 9 Tập 1: Cho ví dụ về hệ phương trình hai ẩn.

Lời giải:

${\begin{cases} 2 x + y = 1 \\ - x + 4 y = 5 \end{cases}$

Luyện tập 4 trang 17 Toán 9 Tập 1: Cho hệ phương trình: ${\begin{cases} 2 x - 5 y = - 2 \\ x + y = 6 \end{cases}$ .

Kiểm tra xem cặp số nào sau đây là nghiệm của phương trình đã cho:

a. $(3; 3)$ ;

b. $(4; 2)$ .

Lời giải:

a. Thay giá trị $x = 3; y = 3$ vào mỗi phương trình trong hệ ta có:

$\begin{array}{l} 2.3 - 5.3 = - 9 \neq - 2; \\ 3 + 3 = 6 . \end{array}$

Do đó, cặp số $(3; 3)$ không là nghiệm của phương trình thứ nhất trong hệ phương trình đã cho.

Vậy cặp số $(3; 3)$ không là nghiệm của hệ phương trình đã cho.

b. Thay giá trị $x = 4; y = 2$ vào mỗi phương trình trong hệ ta có:

$\begin{array}{l} 2.4 - 5.2 = - 2; \\ 4 + 2 = 6 . \end{array}$

Suy ra cặp số $(4; 2)$ là nghiệm của từng phương trình trong hệ.

Do đó cặp số $(4; 2)$ là nghiệm của hệ phương trình đã cho.

Bài tập

Bài 1 trang 17 Toán 9 Tập 1: Trong các cặp số $(8; 1), (- 3; 6), (4; - 1), (0; 2)$ cho biết cặp số nào là nghiệm của mỗi phương trình sau:

a. $x - 2 y = 6$ ;

b. $x + y = 3$ .

Lời giải:

+ Thay cặp số $(8; 1)$ vào phương trình $x - 2 y = 6$ ta được: $8 - 2.1 = 6$ .

+ Thay cặp số $(- 3; 6)$ vào phương trình $x - 2 y = 6$ ta được: $- 3 - 2.6 = - 15 \neq 6$ .

+ Thay cặp số $(4; - 1)$ vào phương trình $x - 2 y = 6$ ta được: $4 - 2. (- 1) = 6$ .

+ Thay cặp số $(0; 2)$ vào phương trình $x - 2 y = 6$ ta được: $0 - 2.2 = - 4 \neq 6$ .

Vậy các cặp số $(8; 1), (4; - 1)$ là nghiệm của phương trình $x - 2 y = 6$ .

+ Thay cặp số $(8; 1)$ vào phương trình $x + y = 3$ ta được: $8 + 1 = 9 \neq 3$ .

+ Thay cặp số $(- 3; 6)$ vào phương trình $x + y = 3$ ta được: $- 3 + 6 = 3$ .

+ Thay cặp số $(4; - 1)$ vào phương trình $x + y = 3$ ta được: $4 - 1 = 3$ .

+ Thay cặp số $(0; 2)$ vào phương trình $x + y = 3$ ta được: $0 + 2 = 2 \neq 3$ .

Vậy các cặp số $(- 3; 6), (4; - 1)$ là nghiệm của phương trình $x + y = 3$ .

Bài 2 trang 17 Toán 9 Tập 1: Cho hệ phương trình: ${\begin{cases} x + 2 y = 1 \\ 3 x - 2 y = 3 . \end{cases}$

Trong các cặp số sau, cặp số nào là nghiệm của hệ phương trình đã cho?

a. $(3; - 1)$ ;

b. $(1; 0)$ .

Lời giải:

a. Thay $x = 3; y = - 1$ vào mỗi phương trình trong hệ, ta có:

$\begin{array}{l} 3 + 2. (- 1) = 1; \\ 3.3 - 2. (- 1) = 12 \neq 3 . \end{array}$

Do đó, cặp số $(3; - 1)$ không là nghiệm của phương trình thứ hai trong hệ phương trình đã cho.

Vậy cặp số $(3; - 1)$ không là nghiệm của hệ phương trình đã cho.

b. Thay $x = 1; y = 0$ vào mỗi phương trình trong hệ, ta có:

$\begin{array}{l} 1 + 2.0 = 1; \\ 3.1 - 2.0 = 3 . \end{array}$

Suy ra cặp số $(1; 0)$ là nghiệm của từng phương trình trong hệ.

Vậy cặp số $(3; - 1)$ không là nghiệm của hệ phương trình đã cho.

Bài 3 trang 17 Toán 9 Tập 1: Nhân dịp tết Trung thu, một doanh nghiệp dự định sản xuất hai loại bánh: bánh nướng và bánh dẻo. Lượng đường cần cho mỗi chiếc bánh nướng, bánh dẻo lần lượt là 60g, 50g. Gọi $x$ và $y$ lần lượt là số lượng bánh nướng, bánh dẻo mà doanh nghiệp dự định sản xuất để lượng đường sản xuất bánh là 500kg. Viết phương trình bậc nhất hai ẩn $x, y$ và chỉ ra ba nghiệm của phương trình đó.

Toán 9 Bài 2 (Cánh diều): Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn (ảnh 1)

Lời giải:

+ Lượng đường cần cho $x$ chiếc bánh nướng là: $50 x (g)$ ;

+ Lượng đường cần cho $y$ chiếc bánh dẻo là: $60 y (g)$ ;

+ Tổng lượng đường cần dùng là là: $50 x + 60 y (g)$ ;

+ Lượng đường doanh nghiệp dự định sản xuất là: $500 k g = 500 000 g$ .

Suy ra Ta có phương trình: $50 x + 60 y = 500 000$ .

+ Ba nghiệm của phương trình là: $(9760; 200), (8200; 1500), (6400; 3000)$ .

Bài 4 trang 17 Toán 9 Tập 1: Năm bạn Châu, Hà, Khang, Minh, Phong cùng đi mua sticker để trang trí vở. Có hai loại sticker: loại I giá 2 nghìn đồng/chiếc và loại II giá 3 nghìn đồng/chiếc. Mỗi bạn mua 1 chiếc và tổng số tiền năm bạn phải trả là 12 nghìn dồng. Gọi $x$ và $y$ lần lượt là số sticker loại I và loại II mà năm bạn đã mua.

a. Viết hệ phương trình bậc nhất hai ẩn $x; y$ .

b. Cặp số $(3; 2)$ có phải là nghiệm của hệ phương trình câu a hay không? Vì sao?

Lời giải:

+ Năm bạn, mỗi bạn mua 1 chiếc nên ta có: $x + y = 5$ ;

+ Tổng số tiền năm bản phải trả là 12 nghìn đồng, nên ta có: $2 x + 3 y = 12$ .

+ Ta có hệ phương trình: ${\begin{cases} x + y = 5 \\ 2 x + 3 y = 12 \end{cases}$ .

b. Thay $x = 3; y = 2$ vào từng phương trình của hệ, ta có:

$\begin{array}{l} 3 + 2 = 5; \\ 2.3 + 3.2 = 12 . \end{array}$

Vậy cặp số $(3; 2)$ là nghiệm của hệ phương trình ở câu a.

Bài 5 trang 18 Toán 9 Tập 1: Để chuẩn bị cho buổi liên hoan của gia đình, bác Ngọc mua hai loại thực phẩm là thịt lợn và cá chép. Giá tiền thịt lợn là 130 nghìn đồng/kg, giá tiền cá chép là 50 nghìn đồng/kg. Bác Ngọc đã chi 295 nghìn đồng để mua 3,5kg hai loại thực phẩm trên. Gọi $x$ và $y$ lần lượt là số kilôgam thịt lợn và cá chép mà bác Ngọc đã mua.

a. Viết hệ phương trình bậc nhất hai ẩn $x, y$ .

b. Cặp số $(1, 5; 2)$ có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Lời giải:

+ Bác Ngọc mua tổng 3,5kg hai loại thực phẩm nên ta có phương trình: $x + y = 3, 5$ ;

+ Bác Ngọc đã chi 295 nghìn đồng để mua hai loại thực phẩm nên ta có phương trình: $130 x + 50 y = 295$ ;

Suy ra Ta có hệ phương trình: ${\begin{cases} x + y = 3, 5 \\ 130 x + 50 y = 295 \end{cases}$ .

Thay $x = 1, 5; y = 2$ vào từng phương trình của hệ, ta có

$\begin{array}{l} 1, 5 + 2 = 3, 5 \\ 130.1, 5 + 50.2 = 295 \end{array}$

Vậy cặp số $(1, 5; 2)$ là nghiệm của hệ phương trình ở câu a.

Bài 6 trang 18 Toán 9 Tập 1: Người ta cần sơn hai loại sản phẩm A, B bằng hai loại sơn: sơn xanh, sơn vàng. Lượng sơn để sơn mỗi loại sản phẩm đó được cho ở Bảng 1 (đơn vị: kg/1 sản phẩm).

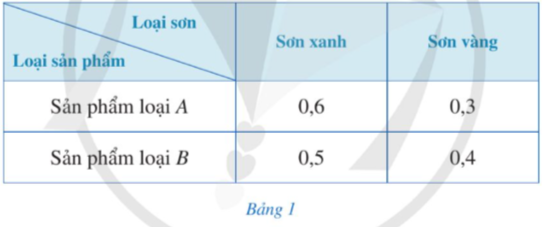
Toán 9 Bài 2 (Cánh diều): Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn (ảnh 1)

Người ta dự định sử dụng 85kg sơn xanh và 50kg sơn vàng để sơn tất cả các sản phẩm của hai loại đó. Gọi $x; y$ lần lượt là số sản phẩm loại A, số sản phẩm loại B được sơn.

a. Viết hệ phương trình bậc nhất hai ẩn x, y.

b. Cặp số $(100; 50)$ có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Lời giải:

+ Sử dụng 85kg sơn Xanh để sơn hai loại sản phẩm A, B nên ta có: $0, 6 x + 0, 5 y = 85$ ;

+ Sử dụng 50kg sơn Vàng để sơn hai loại sản phẩm A, B nên ta có: $0, 3 x + 0, 4 y = 50$ .

Suy ra Ta có hệ phương trình: ${\begin{cases} 0, 6 x + 0, 5 y = 85 \\ 0, 3 x + 0, 4 y = 50 \end{cases}$ .

b. Thay $x = 100, y = 50$ vào hai phương trình của hệ phương trình ta có:

$\begin{array}{l} 0, 6.100 + 0, 5.50 = 85 \\ 0, 3.100 + 0, 4.50 = 50 \end{array}$

Vậy cặp số $(100; 50)$ là nghiệm của hệ phương trình ở câu a.

Xem thêm các bài giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:

§1. Phương trình quy về phương trình bậc nhất một ẩn

§2. Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

§3. Giải hệ hai phương trình bậc nhất hai ẩn

Bài tập cuối chương 1

§1. Bất đẳng thức

§2. Bất phương trình bậc nhất một ẩn

Lý thuyết Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn

1. Phương trình bậc nhất hai ẩn

Khái niệm phương trình bậc nhất hai ẩn

Phương trình bậc nhất hai ẩn x và y là hệ thức dạng

$a x + b y = c$ ,

trong đó a, b và c là các số cho trước, $a \neq 0$ hoặc $b \neq 0$ .

Ví dụ: $2 x + 3 y = 4$ , $0 x + 2 y = 3$ , $x + 0 y = 2$ là các phương trình bậc nhất hai ẩn.

Nghiệm của phương trình bậc nhất hai ẩn

Cho phương trình bậc nhất hai ẩn x, y: $a x + b y = c$ .

Nếu $a x_{0} + b y_{0} = c$ là một khẳng định đúng thì cặp số $(x_{0}; y_{0})$ được gọi là một nghiệm của phương trình $a x + b y = c$ .

Ví dụ: Cặp số $(- 1; 2)$ là nghiệm của phương trình $2 x + 3 y = 4$ vì $2. (- 1) + 3.2 = - 2 + 6 = 4$ .

Cặp số $(1; 2)$ không là nghiệm của phương trình $2 x + 3 y = 4$ vì

$2.1 + 3.2 = 2 + 6 = 8 \neq 4$ .

Chú ý:

Ta cũng áp dụng được quy tắc chuyển vế, quy tắc nhân đã biết ở phương trình bậc nhất một ẩn để biến đổi phương trình bậc nhất hai ẩn.

Biểu diễn nghiệm trên mặt phẳng tọa độ Oxy

- Trong mặt phẳng tọa độ Oxy, mỗi nghiệm của phương trình $a x + b y = c$ được biểu diễn bởi một điểm. Nghiệm $(x_{0}; y_{0})$ được biểu diễn bởi điểm có tọa độ $(x_{0}; y_{0})$ .

- Mỗi nghiệm của phương trình $a x + 0 y = c (a \neq 0)$ được biểu diễn bởi điểm có tọa độ $(\frac{c}{a}; y_{0})$ $(y_{0} \in R)$ nằm trên đường thẳng $d_{1} : x = \frac{c}{a}$ . Đường thẳng $d_{1}$ là đường thẳng đi qua điểm $\frac{c}{a}$ trên trục Ox và vuông góc với trục Ox.

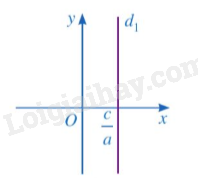
Lý thuyết Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn (Cánh diều 2024) | Lý thuyết Toán 9 (ảnh 1)

- Mỗi nghiệm của phương trình $0 x + b y = c (b \neq 0)$ được biểu diễn bởi một điểm có tọa độ $(x_{0}; \frac{c}{b}) (x_{0} \in R)$ nằm trên đường thẳng $d_{2} : y = \frac{c}{b}$ . Đường thẳng $d_{2}$ là đường thẳng đi qua điểm $\frac{c}{b}$ trên trục Oy và vuông góc với trục Oy.

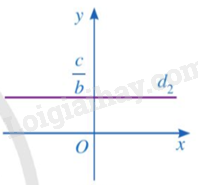
Lý thuyết Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn (Cánh diều 2024) | Lý thuyết Toán 9 (ảnh 2)

- Mỗi nghiệm của phương trình $a x + b y = c (a \neq 0, b \neq 0)$ được biểu diễn bởi một điểm nằm trên đường thẳng $d_{3} : y = - \frac{a}{b} x + \frac{c}{b}$ .

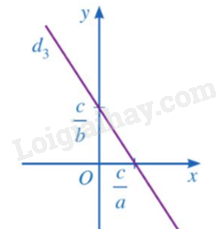
Lý thuyết Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn (Cánh diều 2024) | Lý thuyết Toán 9 (ảnh 3)

Ví dụ:

Nghiệm của phương trình $- 3 x + y = 2$ được biểu diễn bởi đường thẳng d: $y = 3 x + 2$ .

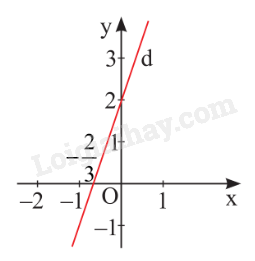
Lý thuyết Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn (Cánh diều 2024) | Lý thuyết Toán 9 (ảnh 4)

Nghiệm của phương trình $0 x + y = - 2$ được biểu diễn bởi đường thẳng d: $y = - 2$ vuông góc với Oy tại điểm $M (0; - 2)$ .

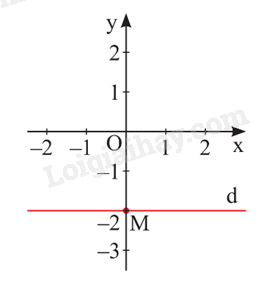
Lý thuyết Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn (Cánh diều 2024) | Lý thuyết Toán 9 (ảnh 5)

Nghiệm của phương trình $2 x + 0 y = 3$ được biểu diễn bởi đường thẳng d: $x = 1, 5$ vuông góc với Ox tại điểm $N (1, 5; 0)$ .

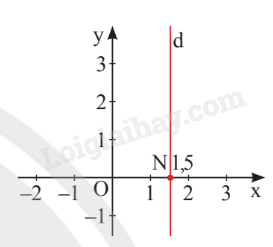
Lý thuyết Phương trình bậc nhất hai ẩn. Hệ hai phương trình bậc nhất hai ẩn (Cánh diều 2024) | Lý thuyết Toán 9 (ảnh 6)

2. Hệ hai phương trình bậc nhất hai ẩn

Khái niệm hệ hai phương trình bậc nhất hai ẩn

Hệ hai phương trình bậc nhất hai ẩn x, y có dạng:

${\begin{cases} a x + b y = c \\ a^{'} x + b^{'} y = c^{'} \end{cases} (I)$ ,

ở đó mỗi phương trình $a x + b y = c$ và $a^{'} x + b^{'} y = c^{'}$ đều là phương trình bậc nhất hai ẩn.

Ví dụ: Hệ phương trình ${\begin{cases} 2 x - y = 0 \\ x + y = 3 \end{cases}$ , ${\begin{cases} 3 x = 1 \\ x - y = 3 \end{cases}$ , ${\begin{cases} 4 x - y = 3 \\ 3 y = 6 \end{cases}$ là các hệ phương trình bậc nhất hai ẩn.