Giải SGK Toán 9 Bài 2 (Cánh diều ): Bất phương trình bậc nhất một ẩn

Van Anh Ngày: 23-09-2024 Lớp 9

737

Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 2: Bất phương trình bậc nhất một ẩn chi tiết sách Toán 9 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 2: Bất phương trình bậc nhất một ẩn

Khởi động trang 35 Toán 9 Tập 1: Giả sử mỗi hộp màu tím đặt trên đĩa cân ở Hình 1 đều có khối lượng là $x$ , còn mỗi hộp màu vàng đều có khối lượng 1 kg. Khi đó, hai biểu thức biểu thị (theo $x$ ) tổng khối lượng của các hộp xếp ở đĩa cân bên trái, đĩa cân bên phải lần lượt là $3 x + 4, x + 6$ . Do đó cân lệch về bên trái nên ta có hệ thức: $3 x + 4 > x + 6$ .

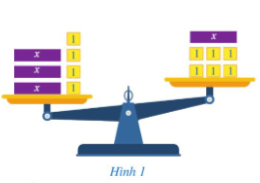
Toán 9 Bài 2 (Cánh diều): Bất phương trình bậc nhất một ẩn (ảnh 1)

Trong toán học, hệ thức $3 x + 4 > x + 6$ được gọi là gì?

Lời giải:

Trong toán học hệ thức $3 x + 4 > x + 6$ được gọi là bất phương trình với ẩn x.

Hoạt động 1 trang 35 Toán 9 Tập 1: Xét hệ thức $3 x + 4 > x + 6$ (1) nêu ở bài toán ở phần mở đầu.

a. Các biểu thức $3 x + 4, x + 6$ có phải là hai biểu thức của cùng một biến $x$ hay không?

b. Khi thay giá trị $x = 5$ vào hệ thức (1), ta có được một khẳng định đúng hay không?

Lời giải:

a. Biểu thức $3 x + 4, x + 6$ là hai biểu thức của cùng một biến $x$ .

+ Thay $x = 5$ vào vế trái của hệ thức (1) ta được: $3.5 + 4 = 19$ .

+ Thay $x = 5$ vào vế phải của hệ thức (1) ta được: $5 + 6 = 11$ .

+ Do $19 > 11$ nên ta được một khẳng định đúng.

1. Mở đầu về bất phương trình một ẩn

Luyện tập 1 trang 36 Toán 9 Tập 1: Cho biết giá trị $x = 3$ là nghiệm của bất phương trình nào trong các bất phương trình sau:

a. $5 x + 4 > 4 x - 12$ ;

b. $x^{2} - 3 x + 5 \leq 4$ .

Lời giải:

a. Khi thay giá trị $x = 3$ vào bất phương trình đã cho, ta được $5.3 + 4 > 4.3 - 12$ là khẳng định đúng. Vậy giá trị $x = 3$ là nghiệm của bất phương trình đã cho.

b. Khi thay giá trị $x = 3$ vào bất phương trình đã cho ta được $3^{2} - 3.3 + 5 \leq 4$ là khẳng định sai. Vậy giá trị $x = 3$ không là nghiệm của bất phương trình đã cho.

2. Bất phương trình bậc nhất một ẩn

Hoạt động 2 trang 36 Toán 9 Tập 1: Cho bất phương trình (ẩn $x$ ): $5 x + 20 > 0$ . Đa thức ở vế trái của bất phương trình đó có bậc bằng bao nhiêu?

Lời giải:

Đa thức của vế trái của bất phương trình có bậc là 1.

Luyện tập 2 trang 36 Toán 9 Tập 1: Nêu hai ví dụ về bất phương trình bậc nhất ẩn $x$ .

Lời giải:

+) $3 x + 4 < 0$

+) $2 x + 5 \geq 0$ .

Luyện tập 3 trang 37 Toán 9 Tập 1: Kiểm tra xem $x = - 7$ có phải là nghiệm của bất phương trình bậc nhất $2 x + 15 \geq 0$ hay không?

Lời giải:

Thay $x = - 7$ , ta có: $2. (- 7) + 15 \geq 0$ là khẳng định đúng.

Vậy $x = - 7$ là nghiệm của bất phương trình $2 x + 15 \geq 0$ .

Hoạt động 3 trang 37 Toán 9 Tập 1: Giải bất phương trình: $4 x - 32 < 0 (2)$ .

Lời giải:

Để giải bất phương trình (2), ta có thể làm như sau:

$\begin{array}{l} 4 x - 32 < 0 \\ 4 x < 32 \\ x < 8 \end{array}$

Vậy nghiệm của bất phương trình (2) là $x < 8$ .

Luyện tập 4 trang 38 Toán 9 Tập 1: Giải các bất phương trình:

a. $- 8 x - 27 < 0$ ;

b. $\frac{5}{4} x + 20 \geq 0$ .

Lời giải:

a. $- 8 x - 27 < 0$

$\begin{array}{l} - 8 x < 27 \\ x > \frac{- 27}{8} \end{array}$

Vậy nghiệm của bất phương trình đã cho là $x > \frac{- 27}{8}$ .

$\begin{array}{l} \frac{5}{4} x + 20 \geq 0 \\ \frac{5}{4} x \geq 20 \\ x \geq 16 \end{array}$

Vậy nghiệm của bất phương trình đã cho là $x \geq 16$ .

Hoạt động 4 trang 38 Toán 9 Tập 1: Giải bất phương trình $3 x + 4 > x + 12$ .

Lời giải:

$\begin{array}{l} 3 x + 4 > x + 12 \\ 3 x + 4 - x - 12 > 0 \\ 2 x - 8 > 0 \\ 2 x > 8 \\ x > 4 \end{array}$

Vậy nghiệm của bất phương trình đã cho là $x > 4$ .

Luyện tập 5 trang 38 Toán 9 Tập 1: Giải bất phương trình $2 (x - 0, 5) - 1, 4 \geq 1, 5 - (x + 1, 2)$ .

Lời giải:

$\begin{array}{l} 2 (x - 0, 5) - 1, 4 \geq 1, 5 - (x + 1, 2) \\ 2 x - 1 - 1, 4 \geq 1, 5 - x - 1, 2 \\ 2 x - 2, 4 - 0, 3 + x \geq 0 \\ 3 x - 2, 7 \geq 0 \\ 3 x \geq 2, 7 \\ x \geq 0, 9 \end{array}$

Vậy nghiệm của bất phương trình đã cho là $x \geq 0, 9$ .

Bài tập

Bài 1 trang 40 Toán 9 Tập 1: Kiểm tra xem số nào là nghiệm của mỗi bất phương trình tương ứng sau đây.

a. $x^{2} - 3 x + 2 > 0$ với $x = - 3; x = 1, 5$ .

b. $2 - 2 x < 3 x + 1$ với $x = \frac{2}{5}; x = \frac{1}{5}$ .

Lời giải:

a. Thay $x = - 3$ , ta có: ${(- 3)}^{2} - 3. (- 3) + 2 > 0$ là khẳng định đúng.

Vậy $x = - 3$ là nghiệm của bất phương trình $x^{2} - 3 x + 2 > 0$ .

Thay $x = 1, 5$ , ta có: $1, 5^{2} - 3.1, 5 + 2 > 0$ là khẳng định sai.

Vậy $x = 1, 5$ không là nghiệm của bất phương trình $x^{2} - 3 x + 2 > 0$ .

b. Thay $x = \frac{2}{5}$ , ta có: $2 - 2. \frac{2}{5} < 3. \frac{2}{5} + 1$ là khẳng định đúng.

Vậy $x = \frac{2}{5}$ là nghiệm của bất phương trình $2 - 2 x < 3 x + 1$ .

Thay $x = \frac{1}{5}$ , ta có: $2 - 2. \frac{1}{5} < 3. \frac{1}{5} + 1$ là khẳng định sai.

Vậy $x = \frac{1}{5}$ không là nghiệm của bất phương trình $2 - 2 x < 3 x + 1$ .

Bài 2 trang 40 Toán 9 Tập 1: Giải các bất phương trình:

a. $2 x + 6 > 1$

b. $0, 6 x + 2 > 6 x + 9$

c. $1, 7 x + 4 \geq 2 + 1, 5 x$

Lời giải:

$\begin{array}{l} 2 x + 6 > 1 \\ 2 x > - 5 \\ x > \frac{- 5}{2} \end{array}$

Vậy nghiệm của bất phương trình là $x > \frac{- 5}{2}$ .

$\begin{array}{l} 0, 6 x + 2 > 6 x + 9 \\ 0, 6 x + 2 - 6 x - 9 > 0 \\ - 5, 4 x - 7 > 0 \\ - 5, 4 x > 7 \\ x < - \frac{35}{27} \end{array}$

Vậy nghiệm của bất phương trình là $x < - \frac{35}{27}$ .

$\begin{array}{l} 1, 7 x + 4 \geq 2 + 1, 5 x \\ 1, 7 x + 4 - 2 - 1, 5 x \geq 0 \\ 0, 2 x + 2 \geq 0 \\ 0, 2 x \geq - 2 \\ x \geq - 10 \end{array}$

Vậy nghiệm của bất phương trình là $x \geq - 10$ .

Bài 3 trang 41 Toán 9 Tập 1: Giải các bất phương trình:

a. $\frac{8 - 3 x}{2} - x < 5$

b. $3 - 2 x - \frac{6 + 4 x}{3} > 0$

c. $0, 7 x + \frac{2 x - 4}{3} - \frac{x}{6} > 1$

Lời giải:

$\begin{array}{l} \frac{8 - 3 x}{2} - x < 5 \\ \frac{8 - 3 x}{2} - \frac{2 x}{2} < \frac{5}{2} \\ \frac{8 - 3 x - 2 x}{2} - \frac{5}{2} < 0 \\ \frac{8 - 3 x - 2 x - 5}{2} < 0 \\ \frac{- 5 x + 3}{2} < 0 \\ - 5 x + 3 < 0 \\ - 5 x < - 3 \\ x > \frac{3}{5} \end{array}$

Vậy nghiệm của bất phương trình là $x > \frac{3}{5}$ .

$\begin{array}{l} 3 - 2 x - \frac{6 + 4 x}{3} > 0 \\ \frac{9}{3} - \frac{6 x}{3} - \frac{6 + 3 x}{3} > 0 \\ \frac{9 - 6 x - 6 - 3 x}{3} > 0 \end{array}$

$\begin{array}{l} \frac{- 9 x + 3}{3} > 0 \\ - 9 x > - 3 \\ x < \frac{1}{3} \end{array}$

Vậy nghiệm của bất phương trình là $x < \frac{1}{3}$ .

$\begin{array}{l} 0, 7 x + \frac{2 x - 4}{3} - \frac{x}{6} > 1 \\ \frac{4, 2 x}{6} + \frac{2. (2 x - 4)}{6} - \frac{x}{6} > \frac{1}{6} \\ 4, 2 x + 4 x - 8 - x - 1 > 0 \\ 7, 2 x - 9 > 0 \\ 7, 2 x > 9 \\ x > \frac{5}{4} \end{array}$

Vậy nghiệm của bất phương trình là $x > \frac{5}{4}$ .

Bài 4 trang 41 Toán 9 Tập 1: Tìm $x > 0$ sao cho ở Hình 2 chu vi của hình tam giác lớn hơn chu vi của hình chữ nhật:

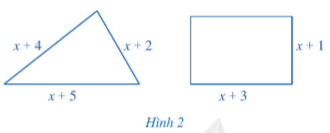
Toán 9 Bài 2 (Cánh diều): Bất phương trình bậc nhất một ẩn (ảnh 1)

Lời giải:

+ Chu vi của hình tam giác là: $x + 4 + x + 5 + x + 2 = 3 x + 11$ .

+ Chu vi của hình chữ nhật là: $2. (x + 3 + x + 1) = 2 (2 x + 4) = 4 x + 8$ .

+ Để chu vi của hình tam giác lớn hơn chu vi của hình chữ nhật ta có bất phương trình:

$\begin{array}{l} 3 x + 11 > 4 x + 8 \\ 3 x + 11 - 4 x - 8 > 0 \\ - x + 3 > 0 \\ - x > - 3 \\ x < 3 \end{array}$

Mà $x > 0$ nên ta có $0 < x < 3$ .

Vậy $x \in {1; 2}$ thỏa mãn yêu cầu đề bài.

Bài 5 trang 41 Toán 9 Tập 1: Một kho chứa 100 tấn xi măng, mỗi ngày đều xuất đi 20 tấn xi măng. Gọi $x$ là số ngày xuất xi măng của kho đó. Tìm $x$ sao cho khối lượng xi măng còn lại trong kho ít nhất là 10 tấn sau $x$ ngày xuất hàng.

Lời giải:

Khối lượng xi măng xuất đi trong $x$ ngày là: $20 x$ (tấn)

Khối lượng xi măng còn lại sau $x$ ngày là: $100 - 20 x$ (tấn)

Để khối lượng xi măng còn lại trong kho ít nhất là 10 tấn thì

$100 - 20 x \geq 10$ .

Giải bất phương trình trên, ta có:

$\begin{array}{l} 100 - 20 x \geq 10 \\ - 20 x \geq 10 - 100 \\ - 20 x \geq - 90 \\ x \leq 4, 5 \end{array}$

Vậy kho phải xuất 4 ngày để số xi măng còn lại trong kho ít nhất là 10 tấn.

Xem thêm các bài giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:

§1. Bất đẳng thức

§2. Bất phương trình bậc nhất một ẩn

Bài tập cuối chương 2

Chủ đề 1. Làm quen với bảo hiểm

§1. Căn bậc hai và căn bậc ba của số thực

§2. Một số phép tính về căn bậc hai của số thực

Lý thuyết Bất phương trình bậc nhất một ẩn

1. Mở đầu về bất phương trình bậc nhất một ẩn

Một bất phương trình với ẩn x có dạng $A (x) > B (x)$ (hoặc $A (x) < B (x), A (x) \geq B (x), A (x) \leq B (x)$ ) trong đó vế trái $A (x)$ và vế phải $B (x)$ là hai biểu thức của cùng một biến x.

Nghiệm của bất phương trình

Khi thay giá trị $x = a$ vào bất phương trình với ẩn x, ta được một khẳng định đúng thì số a (hay giá trị $x = a$ ) gọi là nghiệm của bất phương trình đó.

Giải bất phương trình là tìm tất cả các nghiệm của bất phương trình đó.

Ví dụ:

Số -2 là nghiệm của bất phương trình $2 x - 10 < 0$ vì $2. (- 2) - 10 = - 4 - 10 = - 14 < 0$ .

Số 6 không là nghiệm của bất phương trình $2 x - 10 < 0$ vì $2.6 - 10 = 12 - 10 = 2 > 0$ .

2. Bất phương trình bậc nhất một ẩn

Định nghĩa

Bất phương trình dạng $a x + b > 0$ (hoặc $a x + b < 0, a x + b \geq 0, a x + b \leq 0$ ) với a, b là hai số đã cho và $a \neq 0$ được gọi là bất phương trình bậc nhất một ẩn.

Ví dụ: $3 x + 16 \leq 0$ ; $- 3 x > 0$ là các bất phương trình bậc nhất một ẩn x.

$x^{2} - 4 \geq 0$ không phải là một bất phương trình bậc nhất một ẩn x vì $x^{2} - 4$ là một đa thức bậc hai.

$3 x - 2 y < 2$ không phải là một bất phương trình bậc nhất một ẩn vì đa thức $3 x - 2 y$ là đa thức với hai biến x và y.

Cách giải

Bất phương trình bậc nhất một ẩn $a x + b > 0$ (với $a > 0$ ) được giải như sau:

$\begin{array}{l} a x + b > 0 \\ a x > - b \\ x > \frac{- b}{a} . \end{array}$

Vậy nghiệm của bất phương trình đã cho là $x > \frac{- b}{a}$ .

Bất phương trình bậc nhất một ẩn $a x + b > 0$ (với $a < 0$ ) được giải như sau:

$\begin{array}{l} a x + b > 0 \\ a x > - b \\ x < \frac{- b}{a} . \end{array}$

Vậy nghiệm của bất phương trình đã cho là $x < \frac{- b}{a}$ .

Chú ý: Các bất phương trình $a x + b < 0$ , $a x + b \leq 0$ , $a x + b \geq 0$ với a, b là hai số đã cho và $a \neq 0$ được giải bằng cách tương tự.

Ví dụ: Giải bất phương trình $- 2 x - 4 > 0$

Lời giải: Ta có:

$\begin{array}{l} - 2 x - 4 > 0 \\ - 2 x > 0 + 4 \\ - 2 x > 4 \\ x < 4. (- \frac{1}{2}) \\ x < - 2 \end{array}$

Vậy nghiệm của bất phương trình là $x < - 2$ .

Chú ý: Ta cũng có thể giải được các bất phương trình dạng $a x + b > c x + d; a x + b < c x + d; a x + b \geq c x + d; a x + b \leq c x + d$ bằng cách đưa bất phương trình về dạng $a x + b < 0$ , $a x + b > 0$ , $a x + b \leq 0$ , $a x + b \geq 0$ .