Với giải Bài 2 trang 21 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 3: Giải hệ hai phương trình bậc nhất hai ẩn
Bài 2 trang 21 Toán 9 Tập 1: Giải các hệ phương trình
a)
b)
c)
d)
Lời giải:
a)
Phương trình 0x = vô nghiệm.
Vậy hệ phương trình vô nghiệm.
b)
Vậy hệ phương trình có nghiệm duy nhất là .
c)
Nhân hai vế của phương trình thứ nhất với , ta được
Cộng từng vế 2 phương trình của hệ, ta được , suy ra x = .
Thay x = vào phương trình ta được . Do đó,
y = .
Vậy hệ phương trình có nghiệm duy nhất là .
d)
Nhân hai vế phương trình thứ hai với 2, ta được
Trừ từng vế 2 phương trình của hệ, ta được – (x – y) = - 6 , suy ra (x – y) = 6 (1)
Thay x – y = 6 vào phương trình 2(x + y) + 3(x – y) = 4 ta được 2(x + y) + 18 = 4
Suy ra x + y = - 7 (2)
Từ (1) và (2) ta có hệ phương trình
Vậy hệ phương trình có nghiệm duy nhất là .
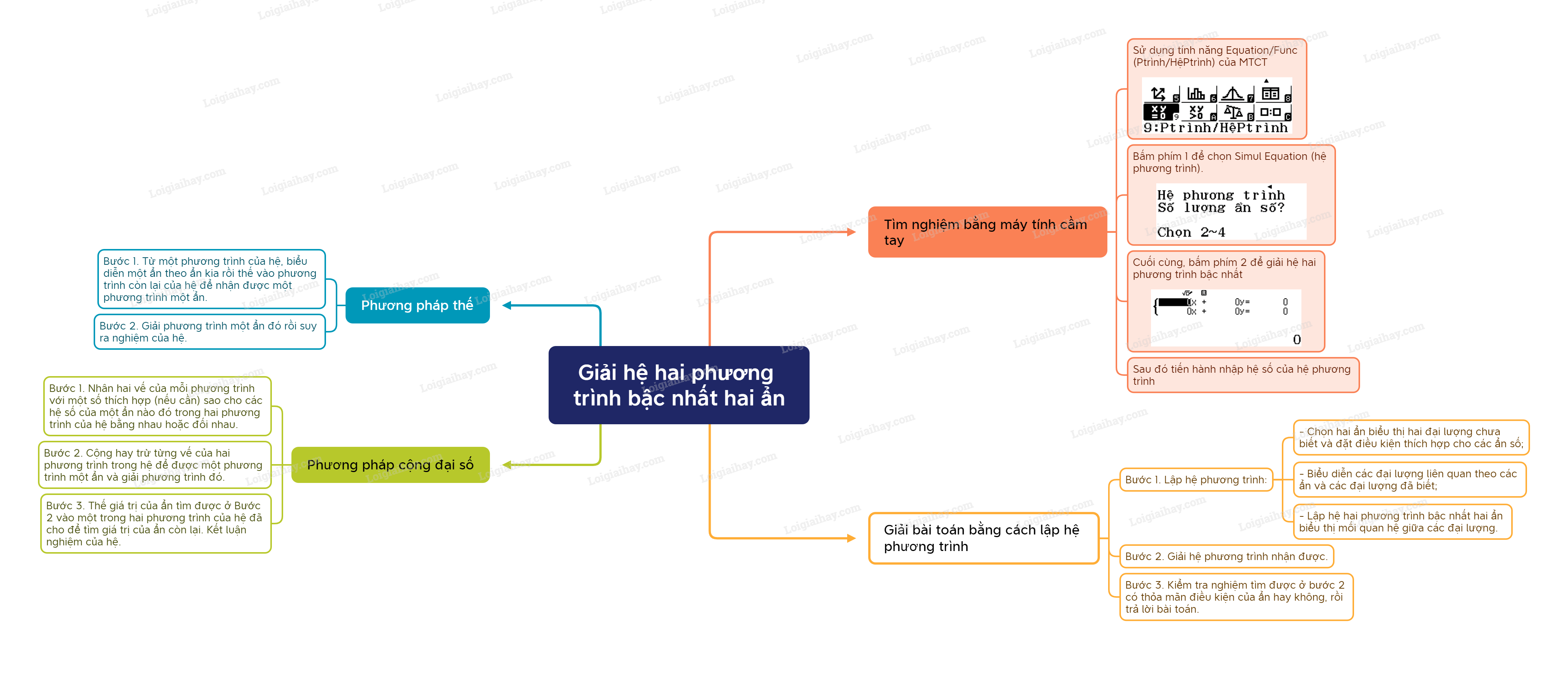
Sơ đồ tư duy Giải hệ hai phương trình bậc nhất hai ẩn
Xem thêm lời giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 1 trang 16 Toán 9 Tập 1: Giải các hệ phương trình:.....
Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Bài 2. Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn
Bài 3. Giải hệ hai phương trình bậc nhất hai ẩn