Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 1: Bất đẳng thức chi tiết sách Toán 9 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 1: Bất đẳng thức

Lời giải:
Ta có x < y.
1. Khái niệm bất đẳng thức
Thực hành 1 trang 26 Toán 9 Tập 1: Hãy chỉ ra các bất đẳng thức diễn tả mỗi khẳng định sau:
a) x nhỏ hơn 5
b) a không lớn hơn b
c) m không nhỏ hơn n
Lời giải:
a) Để diễn tả x nhỏ hơn 5, ta có bất đẳng thức x < 5.
b) Để diễn tả a không lớn hơn b, ta có bất đẳng thức a < b.
c) Để diễn tả m không nhỏ hơn n, ta có bất đẳng thức m > n.
2. Tính chất của bất đẳng thức

Lời giải:
Ta có a > b mà b > c suy ra a > c (bắc cầu).
Hoạt động khám phá 3 trang 26 Toán 9 Tập 1: Thay đổi dấu ? sau bằng dấu thích hợp (>; <):
a) 4 > 1
4 + 15 ? 1 + 15
b) – 10 < - 5
- 10 + (-15) ? – 5 + (-15)
Lời giải:
a) 4 > 1
4 + 15 > 1 + 15
b) – 10 < - 5
- 10 + (-15) < – 5 + (-15)
Thực hành 3 trang 27 Toán 9 Tập 1: So sánh hai số - 3 + 2350 và – 2 + 2350
Lời giải:
Ta có – 3 < - 2. Cộng hai vế của bất đẳng thức với 2350, ta được:
- 3 + 2350 < – 2 + 2350.
Thực hành 4 trang 27 Toán 9 Tập 1: Cho hai số m và n thoả mãn m > n. Chứng tỏ m + 5 > n + 4
Lời giải:
Cộng 5 vào hai vế của bất đẳng thức m > n, ta được:
m + 5 > n + 5 (1)
Cộng n vào hai vế của bất đẳng thức 4 < 5, ta được:
4 + n < 5 + n hay n + 4 < n + 5 (2)
Từ (1) và (2) suy ra m + 5 > n + 4 (bắc cầu).
Lời giải:
Để biểu diễn bạn Toàn lớn tuổi hơn bạn Na, ta có bất đẳng thức
a < b
Sau 3 năm nữa, ta cộng 2 vế của bất đẳng thức với 3, ta được:
a + 3 < b + 3.
Hoạt động khám phá 4 trang 27 Toán 9 Tập 1: Thay mỗi ? sau bằng dấu thích hợp (>;<):
a) 3 > 2
3.17 ? 2.17
b) – 10 < - 2
(-10).5 ? (-1).5
c) 5 > 3
5.(-2) ? 3.(-2)
d) -10 < -2
(-10).(-7) ? (-2).(-7)
Lời giải:
a) 3 > 2
3.17 > 2.17
b) – 10 < - 2
(-10).5 < (-1).5
c) 5 > 3
5.(-2) < 3.(-2)
d) -10 < -2
(-10).(-7) > (-2).(-7)
Thực hành 5 trang 28 Toán 9 Tập 1: Hãy so sánh: (-163).(-75)15 và (-162).(-75)15
Lời giải:
Ta có – 163 < - 162
Nhân cả hai vế bất đẳng thức với (-75)15, ta được:
(-163).(-75)15 > (-162).(-75)15.
Thực hành 6 trang 28 Toán 9 Tập 1: Cho hai số m và n thoả mãn 0 < m2 < n2. Chứng tỏ m2 < 2n2
Lời giải:
Nhân hai vế của bất đẳng thức m2 < n2 với 2, ta được:
2m2 < 2n2 (1)
Vì m2 > 0 nên khi nhân hai vế của bất đẳng thức 2 > , ta được:
2 m2 > m2 (2)
Từ (1) và (2) suy ra m2 < 2n2 (bắc cầu).
Vận dụng 2 trang 28 Toán 9 Tập 1: Cho biết -10m -10n. Hãy so sánh m và n.
Lời giải:
Ta có: -10m -10n. Chia cả 2 vế bất đẳng thức cho (-10), ta được:
m n.
Bài tập
Bài 1 trang 28 Toán 9 Tập 1: Dùng các dấu >,<,, để diễn tả:
a) Tốc độ v đúng quy định với biển báo giao thông ở Hình 4a
b) Trọng tải P của toàn bộ xe khi đi qua cầu đúng quy định với biển báo giao thông ở Hình 4b.
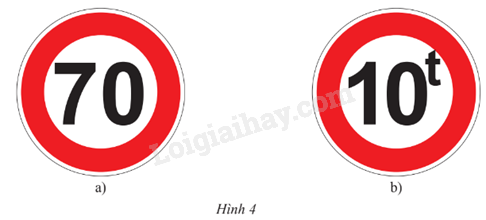
Lời giải:
a) Để diễn tả tốc độ v đúng quy định với biển báo giao thông ở Hình 4a, ta có bất đẳng thức:
v 70
b) Để diễn tả trọng tải P của toàn bộ xe khi đi qua cầu đúng quy định với biển báo giao thông ở Hình 4b, ta có bất đẳng thức:
P 10t.
Bài 2 trang 29 Toán 9 Tập 1: Hãy chỉ ra các bất đẳng thức diễn tả mỗi khẳng định sau:
a) m lớn hơn 8
b) n nhỏ hơn 21
c) x nhỏ hơn hoặc bằng 4
d) y lớn hơn hoặc bằng 0.
Lời giải:
a) Để diễn tả m lớn hơn 8, ta có bất đẳng thức: m > 8
b) Để diễn tả n nhỏ hơn 21, ta có bất đẳng thức: n < 21
c) Để diễn tả x nhỏ hơn hoặc bằng 4, ta có bất đẳng thức: x 4
d) Để diễn tả y lớn hơn hoặc bằng 0, ta có bất đẳng thức: y 0.
Bài 3 trang 29 Toán 9 Tập 1: Hãy cho biết các bất đẳng thức được tạo thành khi:
a) Cộng hai vế của bất đẳng thức m > 5 với – 4;
b) Cộng hai vế của bất đẳng thức x2 y + 1 với 9;
c) Nhân hai vế của bất đẳng thức x > 1 với 3, rồi tiếp tục cộng với 2;
d) Cộng hai vế của bất đẳng thức m - 1 với – 1, rồi tiếp tục cộng với – 7.
Lời giải:
a) Cộng hai vế của bất đẳng thức m > 5 với – 4,ta được:
m – 4 > 5 – 4 suy ra m – 4 > 1
b) Cộng hai vế của bất đẳng thức x2 y + 1 với 9, ta được:
x2 + 9 y + 10
c) Nhân hai vế của bất đẳng thức x > 1 với 3,ta được
3x > 3
Tiếp tục cộng với 2, ta được:
3x + 2 > 5
d) Cộng hai vế của bất đẳng thức m - 1 với – 1,ta được
m – 1 - 2
Tiếp tục cộng với – 7, ta được:
m – 8 - 9.
Bài 4 trang 29 Toán 9 Tập 1: So sánh hai số x và y trong mỗi trường hợp sau:
a) x + 5 > y + 5;
b) – 11x - 11y;
c) 3x – 5 < 3y – 5;
d) – 7x + 1 > - 7y + 1.
Lời giải:
a) x + 5 > y + 5
Trừ cả 2 vế bất đẳng thức với 5, ta được:
x > y
b) – 11x - 11y;
Chia cả hai vế bất đẳng thức với (-11), ta được:
x y
c) 3x – 5 < 3y – 5
Cộng cả 2 vế bất đẳng thức với 5, ta được:
3x < 3y
Chia cả hai vế bất đẳng thức với 3, ta được:
x < y.
d) – 7x + 1 > - 7y + 1.
Trừ cả 2 vế bất đẳng thức với 1, ta được:
– 7x > - 7y
Chia cả hai vế bất đẳng thức với (- 7), ta được:
x < y.
Bài 5 trang 29 Toán 9 Tập 1: Cho hai số a, b thoả mãn a < b. Chứng tỏ:
a) b – a > 0;
b) a – 2 < b – 1
c) 2a + b < 3b
d) – 2a – 3 > - 2b – 3.
Lời giải:
a) Trừ 2 vế của bất đẳng thức a < b cho a, ta được:
0 < b – a hay b – a > 0
b) Trừ 2 vế của bất đẳng thức a < b cho 2, ta được:
a – 2 < b – 2 (1)
Cộng 2 vế của bất đẳng thức - 2 < - 1 cho b , ta được:
- 2 + b < - 1 + b hay b – 2 < b – 1 (2)
Từ (1) và (2) suy ra a – 2 < b – 1
c) Nhân 2 vế của bất đẳng thức a < b cho 2, ta được:
2a < 2b
Cộng 2 vế của bất đẳng thức 2a < 2b cho b, ta được:
2a + b < 3b
d) Nhân 2 vế của bất đẳng thức a < b cho (-2), ta được:
- 2a > - 2b
Cộng 2 vế của bất đẳng thức -2a > -2b cho (-3), ta được:
– 2a – 3 > - 2b – 3.
Đố vui trang 29 Toán 9 Tập 1: Tìm lỗi sai trong lập luận sau:
Bạn Trang nhỏ tuổi hơn bạn Mai, bạn Mai nhẹ cân hơn bạn Tín. Gọi a và b lần lượt là số tuổi của bạn Trang và bạn Mai; b và c là số cân nặng của bạn Mai và bạn Tín. Vì a < b và b < c nên theo tính chất bắc cầu ta suy ra a < c. Vậy bạn Trang nhỏ tuổi hơn bạn Tín.
Lời giải:
Lỗi sai: Gọi số tuổi của bạn Mai = số cân nặng của bạn Mai là b.
Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Bài 2. Bất phương trình bậc nhất một ẩn
Lý thuyết Bất đẳng thức
1. Bất đẳng thức
Nhắc lại thứ tự trên tập số thực
Trên tập số thực, khi so sánh hai số a và b, xảy ra một trong ba trường hợp sau:
- Số a lớn hơn số b, kí hiệu .
- Số a nhỏ hơn số b, kí hiệu .
- Số a bằng số b, kí hiệu .
Khi biểu diễn số thực trên trục số, điểm biểu diễn số bé hơn nằm trước điểm biểu diễn số lớn hơn.
Nếu hoặc , ta viết (ta nói a lớn hơn hoặc bằng b hay a không nhỏ hơn b).
Nếu hoặc , ta viết (ta nói a nhỏ hơn hoặc bằng b hay a không lớn hơn b).
Khái niệm bất đẳng thức
|
Hệ thức dạng (hay , , ) là bất đẳng thức và a được gọi là vế trái, b được gọi là vế phải của bất đẳng thức. |
2. Tính chất của bất đẳng thức
Tính chất bắc cầu
|
Cho ba số a, b, c. Nếu và thì . Nếu và thì . Nếu và thì . Nếu và thì . |
Ví dụ: Vì và nên .
Tính chất liên hệ giữa thứ tự và phép cộng
Khi cộng cùng một số vào hai vế của một bất đẳng thức ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
|
Cho ba số a, b, c. Nếu thì . Nếu thì . Nếu thì . Nếu thì . |
Ví dụ: Vì nên
Tính chất liên hệ giữa thứ tự và phép nhân
- Khi nhân cả hai vế của một bất đẳng thức với cùng một số dương ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
|
Với ba số a, b, c và c > 0, ta có: Nếu thì . Nếu thì . Nếu thì . Nếu thì . |
- Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.
|
Với ba số a, b, c và c < 0, ta có: Nếu thì . Nếu thì . Nếu thì . Nếu thì . |
Ví dụ:
Vì và nên .
Vì và nên .