Với giải Hoạt động 5 trang 86 SGK Toán lớp 10 Cánh diều chi tiết trong Bài 4: Tổng và hiệu của hai vectơ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SGK Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 4: Tổng và hiệu của hai vectơ

Hoạt động 5 trang 86 Toán lớp 10: Cho hai vectơ $\overrightarrow{a},\overrightarrow{b}$ . Lấy một điểm M tùy ý.

a) Vẽ $\overrightarrow{MA}=\overrightarrow{a},\overrightarrow{MB}=\overrightarrow{b},\overrightarrow{MC}=-\overrightarrow{b}$ (Hình 56). 

b) Tổng của hai vectơ $\overrightarrow{a}$ và $\left(-\overrightarrow{b}\right)$ bằng vectơ nào? 

Lời giải:

a) Lấy điểm M tùy ý, qua M vẽ đường thẳng song song với giá của vectơ $\overrightarrow{a}$, trên đường thẳng này về phía cùng hướng với vectơ $\overrightarrow{a}$, lấy điểm A sao cho $\left|\overrightarrow{MA}\right|=\left|\overrightarrow{a}\right|$.

Qua M, tiếp tục vẽ đường thẳng song song với giá của vectơ $\overrightarrow{b}$, trên đường thẳng này về phía cùng hướng với vectơ $\overrightarrow{b}$, lấy điểm B sao cho $\left|\overrightarrow{MB}\right|=\left|\overrightarrow{b}\right|$, về phía ngược hướng với vectơ $\overrightarrow{b}$, lấy điểm C sao cho $\left|\overrightarrow{MC}\right|=\left|\overrightarrow{b}\right|$.

Vậy ta vẽ được các vectơ $\overrightarrow{MA}=\overrightarrow{a},\overrightarrow{MB}=\overrightarrow{b},\overrightarrow{MC}=-\overrightarrow{b}$ như hình vẽ.

b) Tổng của hai vectơ $\overrightarrow{a}$ và $\left(-\overrightarrow{b}\right)$ bằng vectơ $\overrightarrow{MN}$ với N là đỉnh thứ tư của hình bình hành AMCN. 

Lý thuyết Hiệu của hai vectơ

2.1. Hai vectơ đối nhau

Định nghĩa: Vectơ có cùng độ dài và ngược hướng với vectơ $\overrightarrow{\mathrm{a}}$ được gọi là vectơ đối của vectơ $\overrightarrow{\mathrm{a}}$, kí hiệu là –$\overrightarrow{\mathrm{a}}$. Hai vectơ $\overrightarrow{\mathrm{a}}$ và –$\overrightarrow{\mathrm{a}}$ được gọi là hai vectơ đối nhau.

Quy ước: Vectơ đối của vectơ $\overrightarrow{0}$ là vectơ $\overrightarrow{0}$.

Nhận xét:

+) $\overrightarrow{\mathrm{a}}$ + (–$\overrightarrow{\mathrm{a}}$) = (–$\overrightarrow{\mathrm{a}}$) + $\overrightarrow{\mathrm{a}}$ = $\overrightarrow{0}$

+) Hai vectơ $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$ là hai vectơ đối nhau khi và chỉ khi $\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$ = $\overrightarrow{0}$.

+) Với hai điểm A, B, ta có: $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BA}}=\overrightarrow{0}$.

Lưu ý: Cho hai điểm A, B. Khi đó hai vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{BA}}$ là hai vectơ đối nhau, tức là $\overrightarrow{\mathrm{BA}}=-\overrightarrow{\mathrm{AB}}.$  

Chú ý:

– I là trung điểm của đoạn thẳng AB khi và chỉ khi $\overrightarrow{\mathrm{IA}}+\overrightarrow{\mathrm{IB}}=\overrightarrow{0}$.

– G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}=\overrightarrow{0}$.

Ví dụ: Cho hình vuông ABCD có tâm O. Tìm vectơ đối của các vectơ $\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{AO}}$.

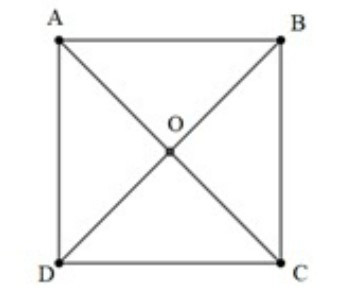
Hướng dẫn giải:

+ Vì $\left|\overrightarrow{\mathrm{BA}}\right|=\left|\overrightarrow{\mathrm{AB}}\right|$= AB và $\overrightarrow{\mathrm{BA}}$ ngược hướng với  $\overrightarrow{\mathrm{AB}}$

⇒ $\overrightarrow{\mathrm{BA}}$ = –$\overrightarrow{\mathrm{AB}}$

Þ $\overrightarrow{\mathrm{BA}}$ là vectơ đối của vectơ $\overrightarrow{\mathrm{AB}}$.

+ Vì AB = CD, AB // CD (ABCD là hình vuông)

⇒ $\left|\overrightarrow{\mathrm{AB}}\right|=\left|\overrightarrow{\mathrm{CD}}\right|$ và $\overrightarrow{\mathrm{CD}}$ ngược hướng với $\overrightarrow{\mathrm{AB}}$

⇒ $\overrightarrow{\mathrm{CD}}$ = –$\overrightarrow{\mathrm{AB}}$

Þ $\overrightarrow{\mathrm{CD}}$ là vectơ đối của vectơ $\overrightarrow{\mathrm{AB}}$.

Vì A, O, C là ba điểm thẳng hàng và OA = OC (ABCD là hình vuông)

⇒ $\overrightarrow{\mathrm{AO}}$ ngược hướng với $\overrightarrow{\mathrm{CO}}$ và $\left|\overrightarrow{\mathrm{AO}}\right|=\left|\overrightarrow{\mathrm{CO}}\right|$

⇒ $\overrightarrow{\mathrm{CO}}$ = –$\overrightarrow{\mathrm{AO}}$

Þ $\overrightarrow{\mathrm{CO}}$ là vectơ đối của $\overrightarrow{\mathrm{AO}}$.

Vậy $\overrightarrow{\mathrm{BA}}$, $\overrightarrow{\mathrm{CD}}$ là vectơ đối của vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{CO}}$ là vectơ đối của $\overrightarrow{\mathrm{AO}}$.

2.2. Hiệu của hai vectơ

Hiệu của hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$, kí hiệu là $\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$, là tổng của vectơ $\overrightarrow{\mathrm{a}}$ và vectơ đối của vectơ $\overrightarrow{\mathrm{b}}$, tức là $\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$ = $\overrightarrow{\mathrm{a}}$ + (–$\overrightarrow{\mathrm{b}}$).

Phép lấy hiệu của hai vectơ được gọi là phép trừ hai vectơ.

Nhận xét: Với ba điểm bất kì A, B, O ta có: $\overrightarrow{\mathrm{AB}}$ = $\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}$.

Ví dụ: Cho 4 điểm A, B, C, D phân biệt. Chứng minh rằng:

$\overrightarrow{\mathrm{AB}}$ – $\overrightarrow{\mathrm{AD}}$ = $\overrightarrow{\mathrm{DC}}-\overrightarrow{\mathrm{BC}}$

Hướng dẫn giải:

Ta có:

$\overrightarrow{\mathrm{AB}}$ – $\overrightarrow{\mathrm{AD}}$ = $\overrightarrow{\mathrm{DB}}$             (áp dụng quy tắc về hiệu hai vectơ) (1)

$\overrightarrow{\mathrm{DC}}-\overrightarrow{\mathrm{BC}}$ = $\overrightarrow{\mathrm{DC}}+\left(-\overrightarrow{\mathrm{BC}}\right)$ = $\overrightarrow{\mathrm{DC}}+\overrightarrow{\mathrm{CB}}$ = $\overrightarrow{\mathrm{DB}}$           (vectơ đối) (2)

Từ (1) và (2) suy ra: $\overrightarrow{\mathrm{AB}}$ – $\overrightarrow{\mathrm{AD}}$ = $\overrightarrow{\mathrm{DC}}-\overrightarrow{\mathrm{BC}}$ (đpcm).